01-学前入门概念:.net与c#
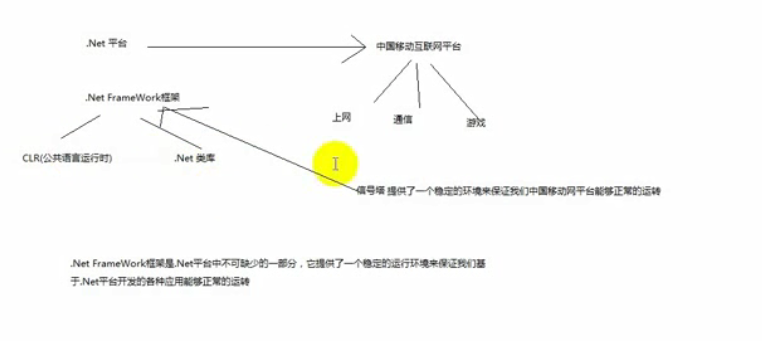
.Net是由(.Net 平台和.Net FrameWork框架)这两部分组成。
.Net FrameWork是由(CLR公共语言运行时和.Net 类库组成)。
.Net FrameWork框架是.Net平台不可缺少的一部分,他提供了一个稳定的运行环境来保证我们基于.Net平台开发的各种应用能够正常的运行。
实例一:

实例二:
C#:是一种编程语言,可以开发基于.Net平台的应用。
01-学前入门概念:.net与c#的更多相关文章
- 087 01 Android 零基础入门 02 Java面向对象 02 Java封装 01 封装的实现 01 封装的概念和特点
087 01 Android 零基础入门 02 Java面向对象 02 Java封装 01 封装的实现 01 封装的概念和特点 本文知识点:封装的概念和特点 说明:因为时间紧张,本人写博客过程中只是对 ...
- C功底挑战Java菜鸟入门概念干货(一)
一.认识Java 1.Java 程序比较特殊,它必须先经过编译,然后再利用解释的方式来运行. 2.Byte-codes 最大的好处是——可越平台运行,可让“一次编写,处处运行”成为可能. 3.使用 ...
- C功底挑战Java菜鸟入门概念干货(二)
(接上篇博文:C功底挑战Java菜鸟入门概念干货(一)) 一.Java面向对象程序设计-类的基本形式 1.“类”是把事物的数据与相关的功能封装在一起,形成的一种特殊结构,用以表达对真实世界的一种抽象概 ...
- Redis 笔记 01:入门篇
Redis 笔记 01:入门篇 ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ...
- 01 Linux入门介绍
一.Linux 初步介绍 Linux的优点 免费的,开源的 支持多线程,多用户 安全性好 对内存和文件管理优越 系统稳定 消耗资源少 Linux的缺点 操作相对困难 一些专业软件以及游戏支持度不足 L ...
- ES 01 - Elasticsearch入门 + 基础概念学习
目录 1 Elasticsearch概述 1.1 Elasticsearch是什么 1.2 Elasticsearch的优点 1.3 Elasticsearch的相关产品 1.4 Elasticsea ...
- java入门概念梳理总结
Java入门学习 简介 public class HelloWorld { public static void main(String []args) { System.out.println(&q ...
- SpringMVC札集(01)——SpringMVC入门完整详细示例(上)
自定义View系列教程00–推翻自己和过往,重学自定义View 自定义View系列教程01–常用工具介绍 自定义View系列教程02–onMeasure源码详尽分析 自定义View系列教程03–onL ...
- Kvm --01 虚拟化基础概念
目录 1. 虚拟化基础概念 01. 什么是虚拟化? 02. 为什么要用虚拟化? 03. 虚拟化在企业中的应用场景? 04. 虚拟化软件介绍 05. Kvm介绍 2. 安装部署Kvm 3. Kvm虚拟机 ...
- 【2016-10-31】【坚持学习】【Day16】【MongoDB】【入门 -概念】
MongoDB 概念解析 不管我们学习什么数据库都应该学习其中的基础概念,在mongodb中基本的概念是文档.集合.数据库,下面我们挨个介绍. 下表将帮助您更容易理解Mongo中的一些概念: SQL术 ...
随机推荐
- Elasticsearch技术解析与实战(七)Elasticsearch批量操作
批量查询 1.如果查询的document是不同index下的不同type种的话 GET /_mget { "docs" : [ { "_index" : &qu ...
- 【LIbreOJ】#6256. 「CodePlus 2017 12 月赛」可做题1
[题意]定义一个n阶正方形矩阵为“巧妙的”当且仅当:任意选择其中n个不同行列的数字之和相同. 给定n*m的矩阵,T次询问以(x,y)为左上角的k阶矩阵是否巧妙.n,m<=500,T<=10 ...
- How to reset XiaoMi bluetooth headphone Youth edition.
To reset the speaker 1. Long press the phone call button to shut off the speaker 2. Connect the char ...
- 伪ajax操作
什么是伪Ajax操作? 说白了就是假的ajax操作,但是它和正常的ajax操作的目的是一样的,把前端的信息发送到后台 先看一下代码吧! ajax.html <form action=" ...
- JWT 拓展
JWT适用场景 https://www.jianshu.com/p/af8360b83a9f 适用于一次性操作的认证,颁布一个很短过期时间的JWT给浏览器. 无状态的JWT无法实现精确的在线人数统计. ...
- 蓝色简单的cms文档管理系统模板——后台
链接:http://pan.baidu.com/s/1qYMwHis 密码:xyiw
- Warning: Permanently added the RSA host key for IP address '192.30.253.113' to the list of known hosts. Permission denied (publickey). fatal: Could not read from remote repository. Please make sure y
这个应该是很多github新手经常出错的问题,这个就是没有在你github上添加一个公钥. 下面就直接说步骤: 1 可以用 ssh -T git@github.com去测试一下 图上可以明显看出缺少了 ...
- python基础===拆分字符串,和拼接字符串
给定某字符,只需要保留其中的有效汉字或者字母,数字之类的.去掉特殊符号或者以某种格式进行拆分的时候,就可以采用re.split的方法.例如 ============================== ...
- linux系统cpu使用100%的命令
for i in `seq 1 $(cat /proc/cpuinfo |grep "physical id" |wc -l)`; do dd if=/dev/zero of=/d ...
- IO的学习与使用
一.IO的学习方法:IO中包含了很多的类,推荐的学习方式是:“举一反三,掌握一种,以此类推”. 二.I/O操作的目标: 输入:从数据源(在数据源和程序之间建立的一个数据流淌的“管道”)中读取数据(文件 ...
