洛谷——P3376 【模板】网络最大流

题目描述

如题，给出一个网络图，以及其源点和汇点，求出其网络最大流。

输入输出格式

输入格式：

第一行包含四个正整数N、M、S、T，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来M行每行包含三个正整数ui、vi、wi，表示第i条有向边从ui出发，到达vi，边权为wi（即该边最大流量为wi）

输出格式：

一行，包含一个正整数，即为该网络的最大流。

输入输出样例

输入样例#1： 复制

4 5 4 3
4 2 30
4 3 20
2 3 20
2 1 30
1 3 40

输出样例#1： 复制

50

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=10，M<=25

对于70%的数据：N<=200，M<=1000

对于100%的数据：N<=10000，M<=100000

样例说明：

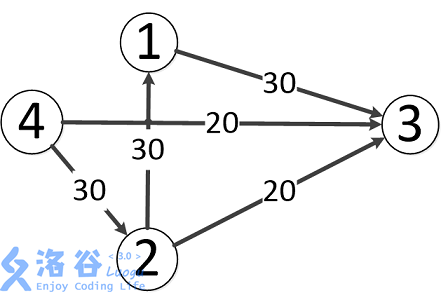
题目中存在3条路径：

4-->2-->3，该路线可通过20的流量

4-->3，可通过20的流量

4-->2-->1-->3，可通过10的流量（边4-->2之前已经耗费了20的流量）

故流量总计20+20+10=50。输出50。

网络流模板

#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 1000010
using namespace std;
queue<int>q;
,ans,s,e;
int to[N],cnt[N],cap[N],lev[N],head[N],nextt[N];
inline int read()
{
    ,f=; char ch=getchar();
    ;ch=getchar();}
    +ch-',ch=getchar();
    return x*f;
}
int add(int x,int y,int z)
{
    to[++tot]=y,cap[tot]=z,nextt[tot]=head[x],head[x]=tot;
    to[++tot]=x,cap[tot]=,nextt[tot]=head[y],head[y]=tot;
}
bool bfs()
{
    while(!q.empty()) q.pop();
    ;i<=n;i++)
    {
        lev[i]=-;
        cnt[i]=head[i];
    }
    q.push(s),lev[s]=;
    while(!q.empty())
    {
        int x=q.front();q.pop();
        for(int i=head[x];i;i=nextt[i])
        {
            int t=to[i];
            &&lev[t]==-)
            {
                lev[t]=lev[x]+;
                q.push(t);
                if(t==e) return true;
            }
        }
    }
    return false;
}
int dinic(int x,int flow)
{
    if(x==e) return flow;
    ,delta;
    for(int &i=cnt[x];i;i=nextt[i])
    {
        int t=to[i];
        &&lev[t]==lev[x]+)
        {
            delta=dinic(t,min(cap[i],flow-rest));
            if(delta)
            {
                rest+=delta;
                cap[i]-=delta;
                cap[i^]+=delta;
                if(rest==flow) break;
            }
        }
    }
    ;
    return rest;
}
int main()
{
    n=read(),m=read(),s=read(),e=read();
    ;i<=m;i++)
    {
        x=read(),y=read(),z=read();
        add(x,y,z);
    }
    while(bfs()) ans+=dinic(s,e);
    printf("%d",ans);
    ;
}