POJ_2155 Matrix 【二维树状数组】

一、题面

POJ2155

二、分析

　　楼教主出的题，是二维树状数组非常好的题，还结合了开关问题(开关变化的次数如果为偶数，状态不变，奇数状态相反）。

　　题意就是给了一个二维的坐标平面，每个点初始值都是0，然后给一个矩形的区域，对该区域的点的状态进行反转。然后在中间插有查询，查该点的状态。

　　其实，还是对反转次数的一个研究，这里为了能快速的查找一个点的反转次数，加上又是二维，且有区间修改，所以选择二维树状数组进行处理，整个二维数组记录的就是反转的次数。

　　每反转一次，就对整个矩形区间进行修改，反转次数加1，最终查询的时候就是查一共反转了多少次，记得取余2，如果是偶数，就不变，是奇数，就变1。

　　注意处理二维树状数组区间更新的时候，假设给的矩形对角线的点为(x1,y1),(x2,y2)。那么更新的时候是

$add(x1,y1,v) + add(x1,y2+1, -v) + add(x2+1, y1, -v)  + add(x2+1,y2+1,v)$

为什么这样，看下图，因为你如果只更新(x1,y1),那么就会更新多的区域，就要想办法减去，但是减了之后，发现又减重了一部分，所以需要又加回来。

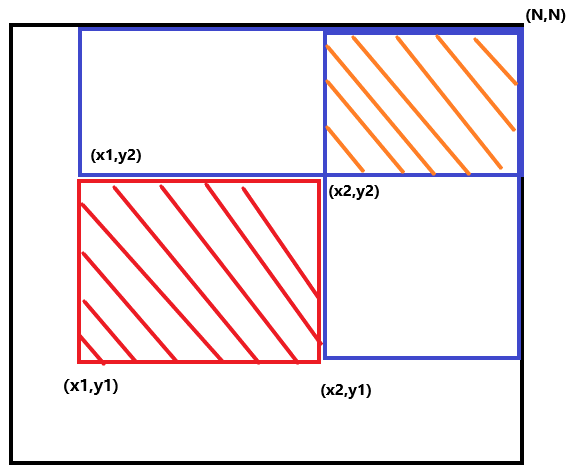
三、AC代码

 #include <cstdio>
 #include <iostream>
 #include <cstring>

 using namespace std;

 const int MAXN = 1e3 + ;

 int BIT[MAXN][MAXN];

 void add(int x, int y, int v)
 {
     for(; x < MAXN; x += x & -x)
     {
         for(int j = y; j < MAXN; j += j & -j)
         {
             BIT[x][j] += v;
         }
     }
 }

 int sum(int x, int y)
 {
     int ans = ;
     for(; x; x -= x & -x)
     {
         for(int j = y; j; j -= j & -j)
         {
             ans += BIT[x][j];
         }
     }
     return ans%;
 }

 void update(int x1, int y1, int x2, int y2, int v)
 {
     add(x1, y1, v);
     add(x2 + , y2 + , v);
     add(x1, y2 + , -v);
     add(x2 + , y1, -v);
 }

 int main()
 {
     //freopen("input.txt", "r", stdin);
     int T;
     scanf("%d", &T);
     while(T)
     {
         int N, Q, x1, y1, x2, y2;
         char c;
         memset(BIT, , sizeof(BIT));
         scanf("%d %d", &N, &Q);
         for(int i = ; i < Q; i++)
         {
             getchar();
             scanf("%c %d %d", &c, &x1, &y1);

             if(c == 'C')
             {
                 scanf("%d %d", &x2, &y2);
                 update(x1, y1, x2, y2, );
             }
             else
             {
                 printf("%d\n", sum(x1, y1));
             }
         }
         if(--T)
             printf("\n");
     }
     return ;
 }