【算法剖析】寻找两个已序数组中的第k大元素

1、问题描述

　　给定两个数组A与B，其大小分别为m、n，假定它们都是已按照增序排序的数组，我们用尽可能快的方法去求两个数组合并后第k大的元素，其中，1\le k\le(m+n)。例如，对于数组A=[1,3,5,7,9]，B=[2,4,6,8]。我们记第k大的数为max_{k-th}，则k=4时，max_{4-th}=4。这是因为排序之后的数组A+B=[1,2,3,4,5,6,7,8,9]，第4大的数是4。我们针对这一个问题进行探讨。

2、算法一

　　第一眼看到这个题的时候，我们能够很快地想出来最基本的一种解法：对数组A和B进行合并，然后求出其第k大的数，即找到答案。合并的过程，我们可以参考归并排序的合并子数组的过程，时间复杂度为O(m+n)。下面给出算法：

int findKthMaxNumOfArrays(int *a,int m,int *b,int n,int k)
{
    int *p=a;
    int *q=b;
    int i=;
    int j=;
    int cur=;
    while(i<m&&j<n)
    {
        if(a[i]<b[j])
        {
            cur++;
            if(cur==k) return a[i];
            i++;
        }
        else
        {
            cur++;
            if(cur==k) return b[j];
            j++;
        }
    }
    while(i<m)
    {
        cur++;
        if(cur==k) return a[i];
        i++;
    }
    while(j<n)
    {
        cur++;
        if(cur==k) return b[j];
        j++;
    }
}

3、算法二

　　实际上算法一的时间复杂度已经是线性的了。可是，是否存在更快的算法能够完成这项任务呢？答案是肯定的，时间复杂度可以缩短到O(log(m+n))时间内。在这种算法中，二分的思想十分重要。我们将数组A分为两半，前一部分的大小为\left \lfloor \frac{m}{2} \right \rfloor，后一部分为m- \left \lfloor \frac{m}{2} \right \rfloor；数组B同时分为这样两部分，第一部分的大小为\left \lfloor \frac{n}{2} \right \rfloor，第二部分的大小为n- \left \lfloor \frac{n}{2} \right \rfloor。如下图所示：

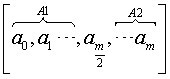
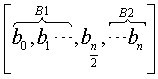
通过a_{\frac{m}{2}}与b_{\frac{n}{2}}，我们将每个数组分为2部分，分别记为A1、A2和B1、B2。假定b_{\frac{n}{2}} \ge a_{\frac{m}{2}}，如果不是，我们只需要交换A、B两个数组即可。接下来，我们看第k大的数落在了哪个区间里面，令t=a_{\frac{m}{2}}+b_{\frac{n}{2}}+1，这个t实际上是包含了A1，a_{\frac{m}{2}}，B1。如果k\le t时，则说明max_{k-th}肯定不在B2里面，这是由于：B2中的所有数\ge b_{\frac{n}{2}}，而b_{\frac{n}{2}} \ge A1,B1中的所有数与a_{\frac{m}{2}}，而这部分数总共有t个，说明b_{\frac{n}{2}}起码是第t+1个，若max_{k-th}出现在B2中，则说明k\ge t+1，与假设矛盾。我们可以得出该结论。因此，在判断之后，我们可以剔除数组B的B2部分，然后再在新数组中寻找；另外，如果k\ge t，则说明max_{k-th}肯定不在A1部分，这部分的证明同上一个证明相同，不再赘述。同样地，在判断之后，我们可以剔除数组A的A1部分，然后再在新数组中寻找。基于这样一种思想，我们每次迭代，都删除了其中一个数组中一半的元素，时间复杂度大约可认为是O(log(m+n))。

　　在实现的时候，我们需要特别注意边界条件，详细的代码如下：

int findKthMaxNumOfArrays(int *A, int m, int *B, int n, int k)
{
        if(m == )return B[k-];
        if(n == )return A[k-];
        int i = m>>, j = n>>, *p, *q, t;
        if(A[i] <= B[j])p = A, q = B;
        else p = B, q = A, swap(i, j), swap(m, n);
        t = i + j + ;
        if(t >= k)return findKthMaxNumOfArrays(p, m, q, j, k);
        else if(t < k)return findKthMaxNumOfArrays(p+i+, m-i-, q, n, k-i-);
}

算法二

4、扩展问题

　　通过算法二，我们很容易地解决一个类似的问题：求两个已序数组A,B的中位数。所谓的中位数，对于一个有n个元素的已序数组，如果n是奇数，则中位数是第\frac{n+1}{2}个元素的值；如果n是偶数，则它的中位数是第\frac{n}{2}与第\frac{n}{2}+1数的平均值。对于m+n为奇数，则利用算法二求第\frac{n+m+1}{2}个元素的值即可，对于m+n为偶数，利用算法二求第\frac{m+n}{2}个与第\frac{m+n}{2}+1个元素的值，求其平均值即可。

　　对于这个问题，在LeetCode中有另外一种解法，但是阅读后发现其需要处理的个别case太多，相比而言没有本文所介绍的算法简洁。如果想要了解，给出链接：http://leetcode.com/2011/03/median-of-two-sorted-arrays.html。