hdu 4940 Destroy Transportation system （无源汇上下界可行流）

Destroy Transportation system

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
http://acm.hdu.edu.cn/showproblem.php?pid=4940

Problem Description

Tom is a commander, his task is destroying his enemy’s
transportation system.

Let’s represent his enemy’s transportation system
as a simple directed graph G with n nodes and m edges. Each node is a city and
each directed edge is a directed road. Each edge from node u to node v is
associated with two values D and B, D is the cost to destroy/remove such edge, B
is the cost to build an undirected edge between u and v.

His enemy can
deliver supplies from city u to city v if and only if there is a directed path
from u to v. At first they can deliver supplies from any city to any other
cities. So the graph is a strongly-connected graph.

He will choose a
non-empty proper subset of cities, let’s denote this set as S. Let’s denote the
complement set of S as T. He will command his soldiers to destroy all the edges
(u, v) that u belongs to set S and v belongs to set T.

To destroy an
edge, he must pay the related cost D. The total cost he will pay is X. You can
use this formula to calculate X: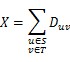

After that, all the edges from S to
T are destroyed. In order to deliver huge number of supplies from S to T, his
enemy will change all the remained directed edges (u, v) that u belongs to set T
and v belongs to set S into undirected edges. (Surely, those edges exist because
the original graph is strongly-connected)

To change an edge, they must
remove the original directed edge at first, whose cost is D, then they have to
build a new undirected edge, whose cost is B. The total cost they will pay is Y.
You can use this formula to calculate Y: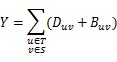

At last, if Y>=X, Tom will
achieve his goal. But Tom is so lazy that he is unwilling to take a cup of time
to choose a set S to make Y>=X, he hope to choose set S randomly! So he asks
you if there is a set S, such that Y<X. If such set exists, he will feel
unhappy, because he must choose set S carefully, otherwise he will become very
happy.

 

Input

There are multiply test cases.

The first line
contains an integer T(T<=200), indicates the number of cases.

For
each test case, the first line has two numbers n and m.

Next m lines
describe each edge. Each line has four numbers u, v, D, B.
(2=<n<=200,
2=<m<=5000, 1=<u, v<=n, 0=<D, B<=100000)

The meaning of
all characters are described above. It is guaranteed that the input graph is
strongly-connected.

 

Output

For each case, output "Case #X: " first, X is the case
number starting from 1.If such set doesn’t exist, print “happy”, else print
“unhappy”.

 

Sample Input

2

3 3

1 2 2 2

2 3 2 2

3 1 2 2

3 3

1 2 10 2

2 3 2 2

3 1 2 2

 

Sample Output

Case #1: happy

Case #2: unhappy

 

Hint

In first sample, for any set S, X=2, Y=4. In second sample. S= {1}, T= {2, 3}, X=10, Y=4.

 

题意：给出一个有向强连通图，每条边有两个值：破坏该边的代价a 和 把该边建成无向边的代价b
问是否存在一个集合S和S的补集T，满足 S到T的割边的 a的总和 > T到S的 割边的 a+b的总和
若存在  输出unhappy， 不存在，输出happy

以a为下界，a+b为上界，判断是否存在无源汇上下界可行流
因为如果存在，流量总和>=下界，<=上界

#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#define N 210
#define M 15000
using namespace std;
int m,n,src,dec,sum,tot;
int a[N];
int front[N],to[M],nextt[M],cap[M];
int lev[N],cur[N];
queue<int>q;
void add(int u,int v,int w)
{
    to[++tot]=v; nextt[tot]=front[u]; front[u]=tot; cap[tot]=w;
    to[++tot]=u; nextt[tot]=front[v]; front[v]=tot; cap[tot]=;
}
bool bfs()
{
    for(int i=src;i<=dec;i++) cur[i]=front[i],lev[i]=-;
    while(!q.empty()) q.pop();
    lev[src]=;
    q.push(src);
    int now;
    while(!q.empty())
    {
        now=q.front(); q.pop();
        for(int i=front[now];i;i=nextt[i])
         if(cap[i]>&&lev[to[i]]==-)
         {
             lev[to[i]]=lev[now]+;
             if(to[i]==dec) return true;
             q.push(to[i]);
         }
    }
    return false;
}
int  dfs(int now,int flow)
{
    if(now==dec) return flow;
    int rest=,delta;
    for(int & i=cur[now];i;i=nextt[i])
     if(cap[i]>&&lev[to[i]]>lev[now])
     {
         delta=dfs(to[i],min(flow-rest,cap[i]));
         if(delta)
         {
             cap[i]-=delta; cap[i^]+=delta;
             rest+=delta; if(rest==flow) break;
        }
     }
     if(rest!=flow) lev[now]=-;
     return rest;
}
int dinic()
{
    int tmp=;
    while(bfs()) tmp+=dfs(src,2e9);
    return tmp;
}
int main()
{
    int T;
    scanf("%d",&T);
    for(int k=;k<=T;k++)
    {
        memset(a,,sizeof(a));
        memset(front,,sizeof(front));
        sum=; tot=;
        scanf("%d%d",&n,&m);
        src=; dec=n+;
        int u,v,c,d;
        for(int i=;i<=m;i++)
        {
            scanf("%d%d%d%d",&u,&v,&c,&d);
            a[v]+=c; a[u]-=c;
            add(u,v,d);
        }
        for(int i=;i<=n;i++)
         if(a[i]<) add(i,dec,-a[i]);
         else if(a[i]>) {add(src,i,a[i]); sum+=a[i];}
        if(dinic()==sum) printf("Case #%d: happy\n",k);
        else printf("Case #%d: unhappy\n",k);
    }
}