安装配置hexo icarus主题配置

安装部分配置hexo icarus主题配置

安装icarus

• 直接下载主题模块放到blog项目 ,blog项目根目录执行

git clone https://github.com/ppoffice/hexo-theme-icarus.git themes/icarus

此时已经下载到项目中。

• 顶级_config.yml中选择icarus主题

  # Extensions
  ## Plugins: https://hexo.io/plugins/
  ## Themes: https://hexo.io/themes/
  theme: icarus
  

• 此时主题已经安装好，清除、编译、部署可以看到效果了

  

配置icarus

• 完全参照官网配置，进行翻译解说

配置文章部分

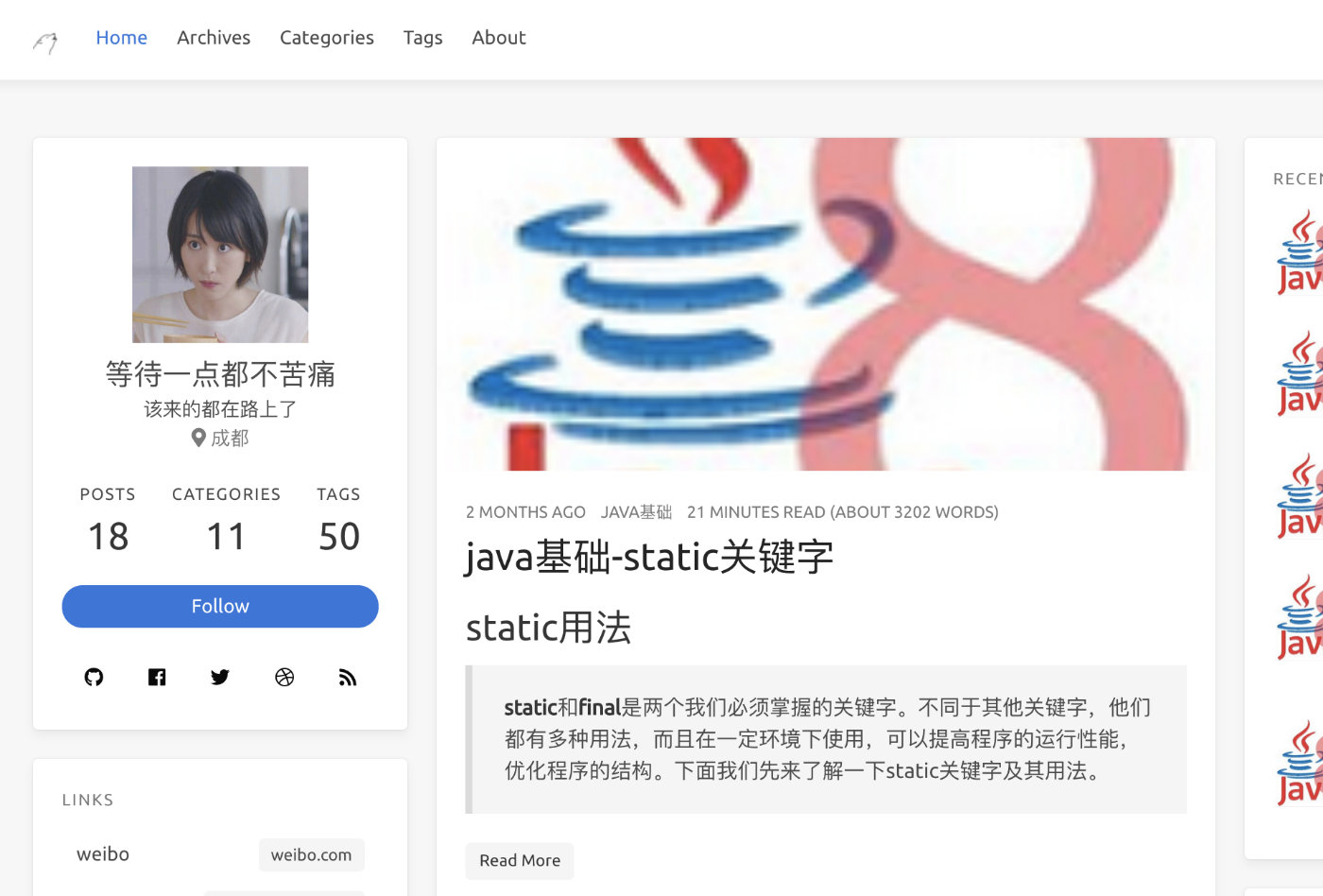
顶部图片添加

icarus 主题中的配置_config.yml中开启图片开关

article:
    thumbnail: true

文章.md文件头中添加图片绝对/相对地址

title: Getting Started with Icarus
thumbnail: /gallery/thumbnails/desert.jpg
// thumbnail:https://raw.githubusercontent.com/removeif/blog_image/master/20190620152744.png
---
Post content...

配置完成后部署显示效果如下(最新文章列表显示缩略图、文章开头显示一张设置图片)

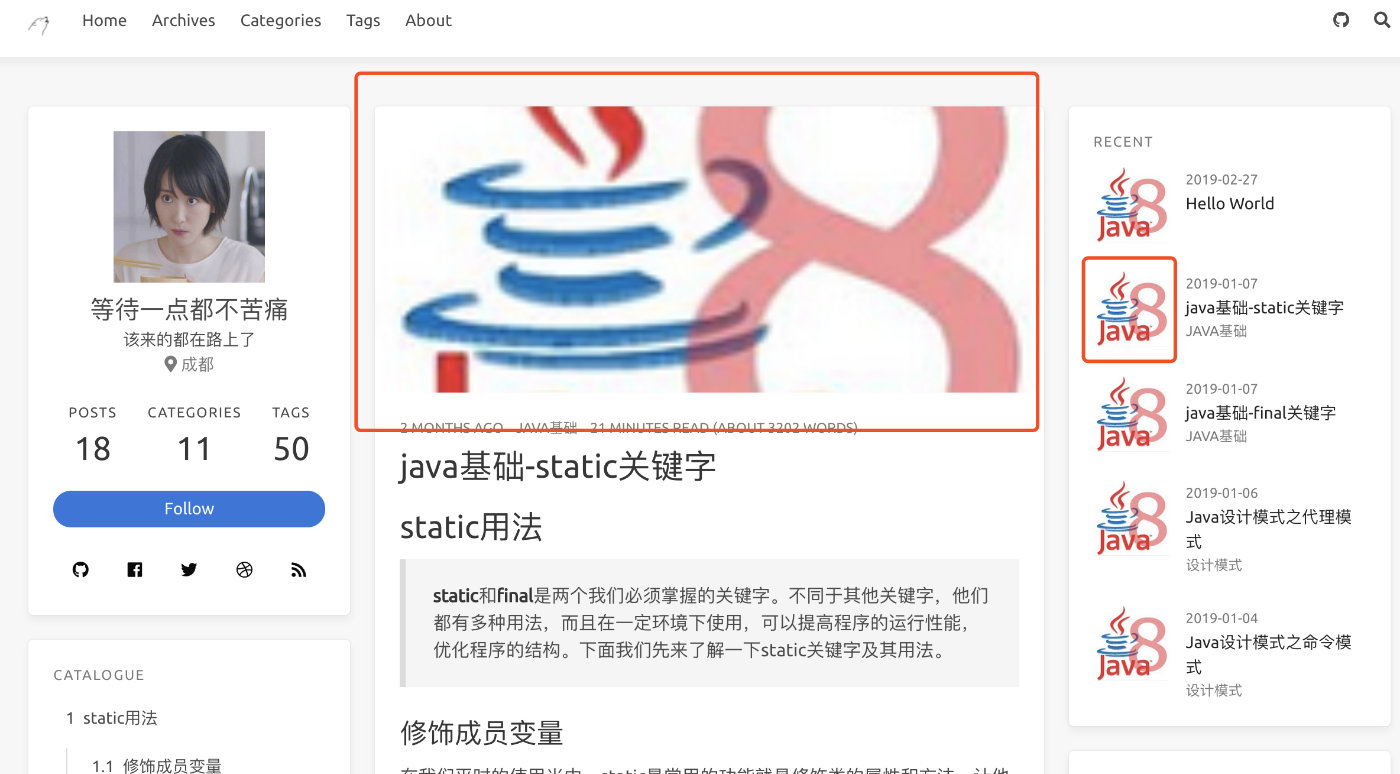
左边文章导航栏开启

icarus 主题中的配置_config.yml中开关

widgets:
    -
        type: toc
        position: left

同事文章顶部加入标签

title: Table of Contents Example
toc: true
---
Post content...

配置效果

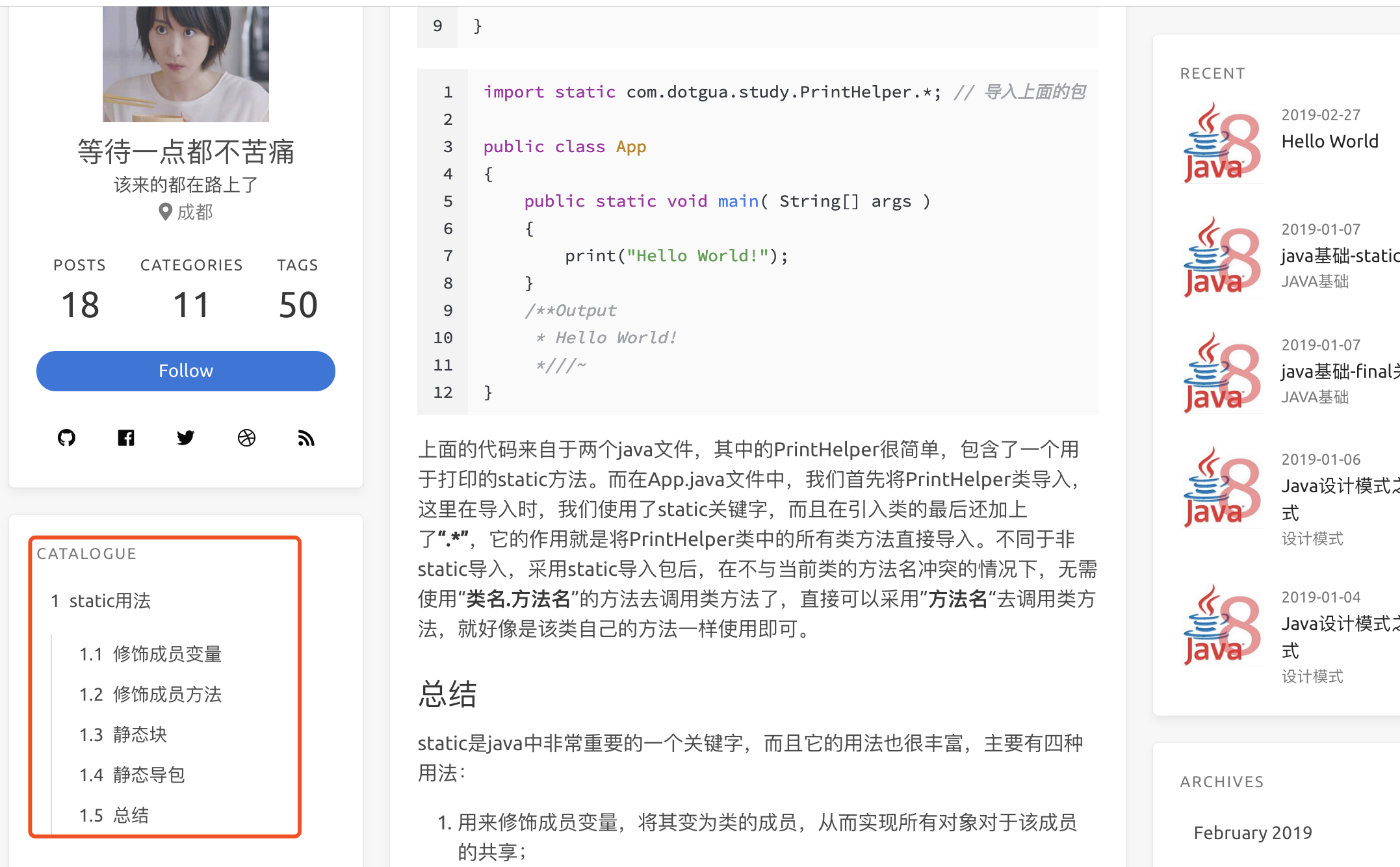
评论系统开启

icarus 主题中的配置_config.yml中开启（部分评论系统需要翻墙才能使用，valine不用翻墙个人推荐，valine安装参考）

comment:
    type: valine
    app_id: xxxxxxxx        # (required) LeanCloud application id
    app_key: xxxxxxxx       # (required) LeanCloud application key
    notify: false           # (optional) receive email notification
    verify: false           # (optional) show verification code
    placeholder: xxxxxxxx   # (optional) comment box placeholder text

开启效果

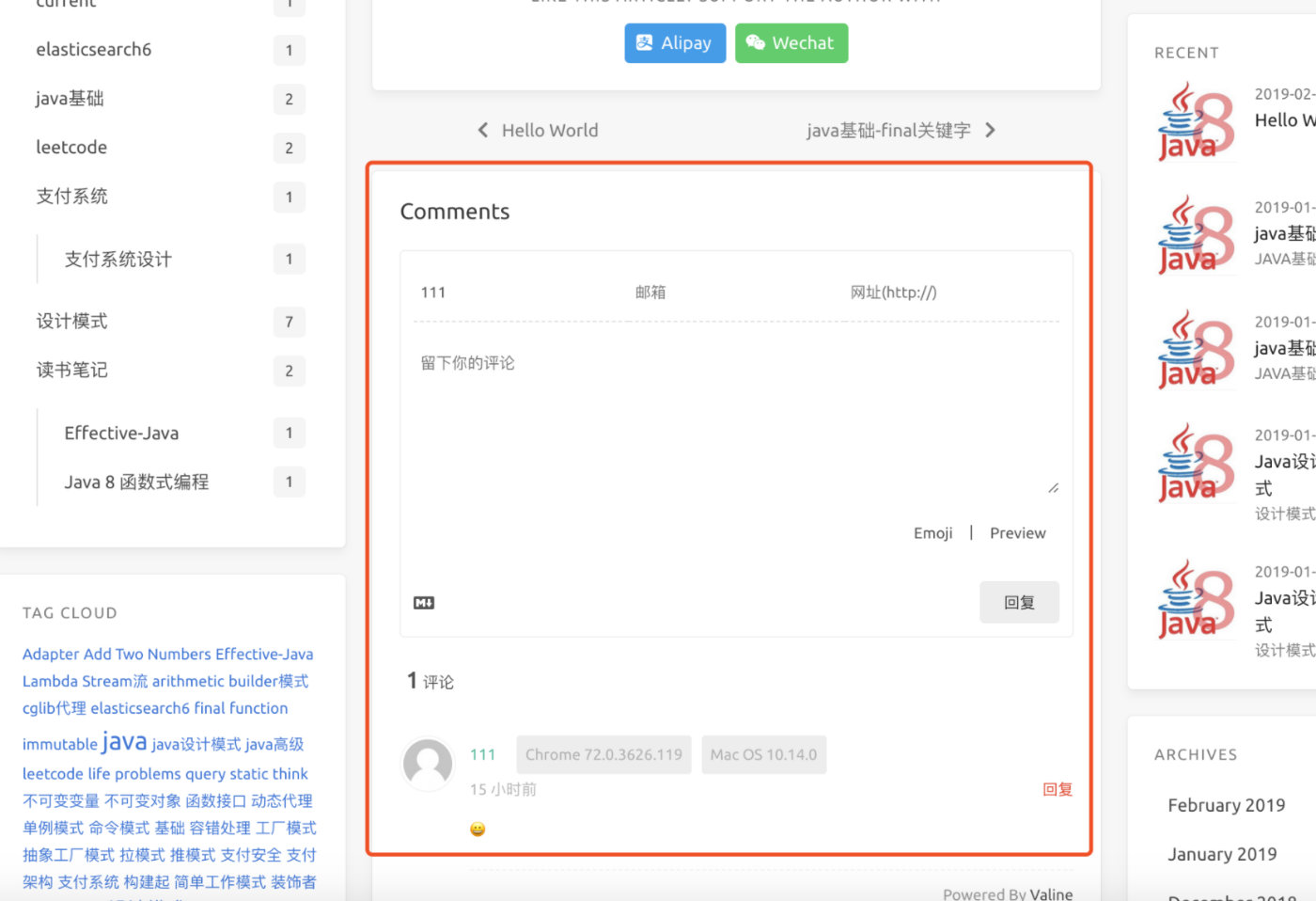
捐赠收款开启

icarus 主题中的配置_config.yml中开启 注意如果默认不配置，编译时有报错，可以# 把它注释掉，不启用功能

donate:
    -
        # Donation entry name
        type: alipay
        # Qrcode image URL
        qrcode: 'https://wx2.sinaimg.cn/large/b5d1b710gy1g0lvxdcwm0j20p011i4bg.jpg'
    -
        # Donation entry name
        type: wechat
        # Qrcode image URL
        qrcode: 'https://wx2.sinaimg.cn/large/b5d1b710gy1g0lvwdcpb5j20u014qgy2.jpg'

开启配置效果如下

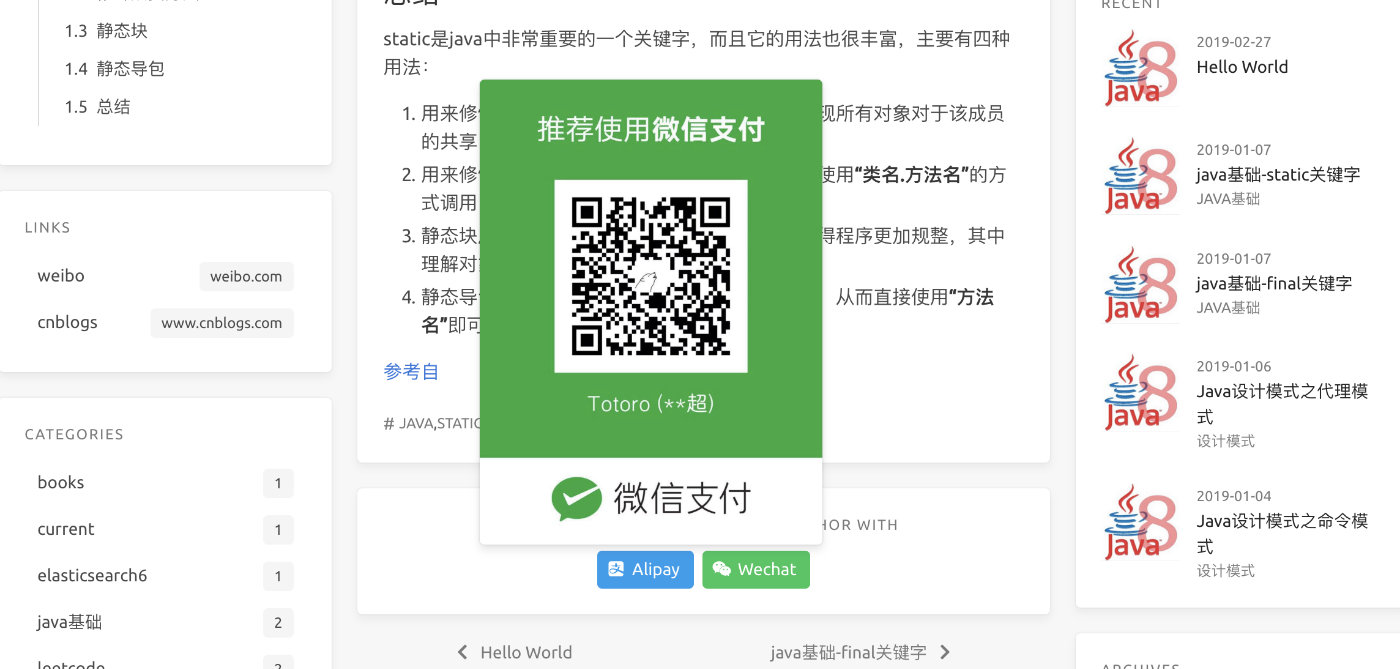
全局搜索开启

icarus 主题中的配置_config.yml中开启,不同的搜索类型需要安装插件参考官网,type: insight此类型不需要安装，已经内置

search:
    type: insight

效果如下

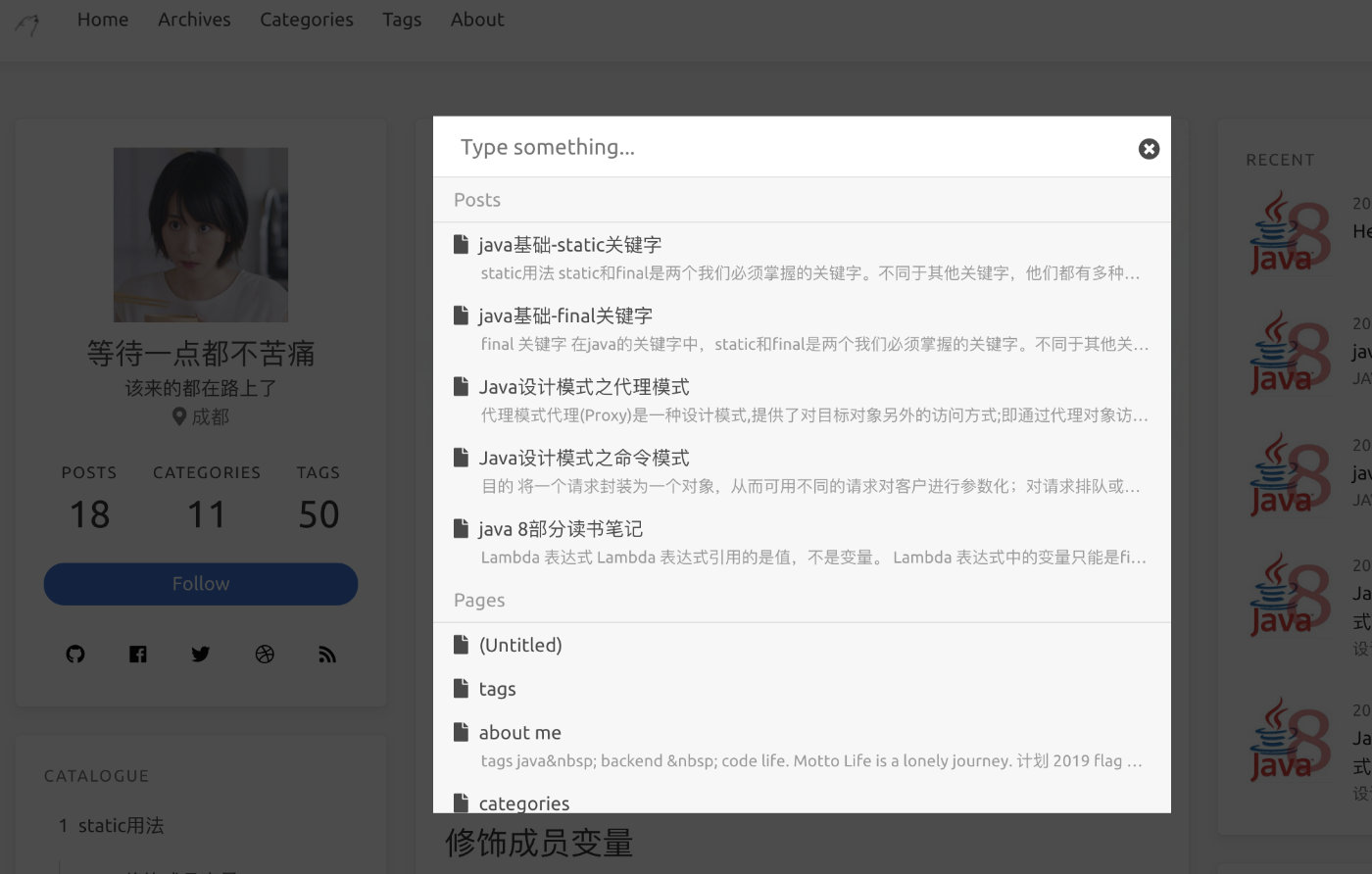
更多配置请参考官网配置

目前配置基本已经够使用，还需要更多配置请参考连接

参考自

欢迎访问 个人博客