[DeeplearningAI笔记]卷积神经网络1.6-1.7构造多通道卷积神经网络

4.1卷积神经网络

觉得有用的话,欢迎一起讨论相互学习~Follow Me

1.6多通道卷积

原理

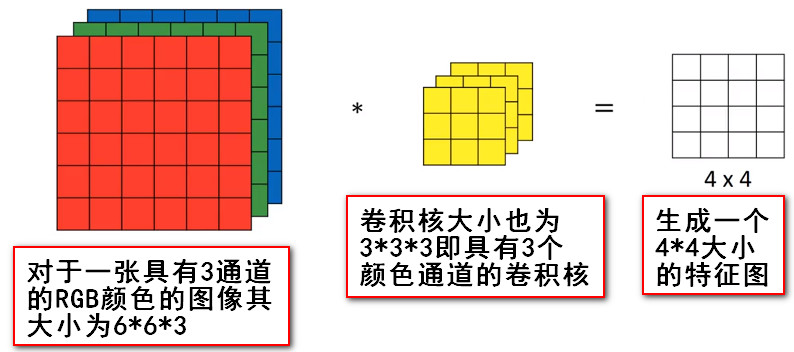
• 对于一个多通道的卷积操作，可以将卷积核设置为一个立方体，则其从左上角开始向右移动然后向下移动，这里设置Padding模式为VALID，步长为1.
• 注意:卷积核中的颜色通道数必须与原始图像的颜色通道数一致。
  
• 如果想要只对红色通道有用的垂直边界，则设置卷积核为:
• 大小为\(3*3*3\)
  
  识别垂直边界过滤器
• 如果想要对图像所有通道识别垂直边界，则设置卷积核为:

• 大小为\(3*3*3\)
  

  多通道多卷积核

• 上文描述了对于多通道单卷积核的卷积操作，如果想要不仅识别图像的垂直边界还想识别图像的水平边界则需要另外构造一个水平边界检测卷积核。

• 此时可以通过两个不同的卷积核得到两个不同的\(4*4\)特征图,将这两个特征图堆叠在一起，则得到了一个\(4*4*2\)的输出立方体。2这个维度来自于两个不同的卷积核

  多通道特征图大小公式

  \[(n*n*n_c)原始图像*(f*f*n_c)卷积核大小=\lfloor\frac{(n+2p-f)}{s}+1\rfloor*\lfloor\frac{(n+2p-f)}{s}+1\rfloor*{n_c}^{'}\]

• 其中n为原始图像大小，\(n_c\)为原始图像通道数，p为Padding填充维度,f为卷积核大小,s为步长
• 当出现得到的结果不是整数时，可以采用向下取整的方式使其维度为整数
• 此处的卷积核意味着一组相同大小的卷积核，不止一个

• \(n_c\)表示通道个数，原始图片和卷积核中通道个数必须相等。\({n_c}^{'}\)表示卷积核个数

---

1.7构造单层卷积层

1. 对于一张\(6*6*3\)的3通道原始图片，经过一个\(3*3*3\)的3通道卷积核得到一个\(4*4\)的图片。然后通过Python的广播机制，将16个像素点都加上一个偏置\(b_1\)。得到的结果通过非线性的激活函数ReLU的得到最终的图片像素点。
2. 对于第二个卷积核，使用相同的步骤，也得到一个\(4*4\)的特征图。然后把这两个矩阵堆叠起来，最终得到一个\(4*4*2\)的矩阵
3. 对于维度，通过卷积层中两个卷积核使一个\(6*6*3\)的图片变成一个\(4*4*2\)的特征图。即：卷积层中卷积核的个数对应了生成的特征图中特征的个数

问题

• 如果一个卷积层中有10个卷积核，卷积核的大小为\(3*3*3\),则加上每个卷积核的偏置一共是\(10*28=280\)个参数。卷积核的参数量和原始图片不相关，即使很大的图片使用以上卷积层，参数量均为280.

总结