在线机器学习FTRL(Follow-the-regularized-Leader)算法介绍

看到好文章，坚决转载！哈哈，学术目的~~

最近几个同事在做推荐平台的项目，都问到怎么实现FTRL算法，要求协助帮忙实现FTRL的算法模块。今天也是有空，赶紧来做个整理。明天还要去上海参加天善智能组织的FLY BI大数据分享会。有兴趣参加线下活动的可以多关注下微博和微信的信息。没事可以多参加分享分享。

现在特别是像做在线学习和CTR这块，应用LR是最广泛的。但是批量处理超大规模的数据集和在线数据流时就遇到了问题，FTRL就是google在这样的背景下研发出来的。在处理非光滑正则化项的凸优化问题上性能非常出色，目前现在阿里也是已经在应用到实际的产品中去了。

当时Google在2013年KDD上发表了FTRL算法后，在业界引起了巨大的反响，国内外各大IT公司纷纷上线该算法。Amazon在他们的搜索广告中上线该算法取得了不错的效果；Yahoo在新闻推荐中也有尝试该算法；国内网易、搜狐、新浪、百度都有上线该算法，也都取得了不错效果；我们目前多个团队也都上线在线学习系统，并取得不错的业务效果。

批处理bacth的离线机器学习方法在每次迭代计算的过程中，需要把全部的训练数据加载到内存中计算（例如计算全局梯度）， 虽然有分布式大规模的机器学习平台，在某种程度上批处理方法对训练样本的数量还是有限制的，onlinelearning不需要cache所有数据，以流式的处理方式可以处理任意数量的样本。研究onlinelearning有两个角度，在线凸优化和在线Bayesian。

在线凸优化方法有很多，像FOBOS算法、RDA、FTRL等；在线Bayesian 方面有比如AdPredictor 算法、基于内容的在线矩阵分解算法等，有兴趣的可以多了解下。包括我们在实际项目中会将FTRL做相应的改进优化，KDD竞赛也是用的FTRL不少。

————————————可恶的分割线———————————————————

—————————未经允许，禁止转载！——————————————————

今天主要介绍三块内容：

1.传统的批量算法、在线学习算法；

2.简单介绍下SGD、FOBOS、RDA等算法；

3.FTRL、FTRL-Proximal的工程实现。

————————————可恶的分割线———————————————————

—————————未经允许，禁止转载！——————————————————

Part 1：

Online learning定义：
Online learning主要指每次来一个样本，利用一个迭代方法更新模型变量，使得当前期望loss最小。

传统算法特点：
【传统Batch算法】

批量算法中每次迭代对全体训练数据集进行计算（例如计算全局梯度），优点是精度和收敛还可以，缺点是无法有效处理大数据集（此时全局梯度计算代价太大），且没法应用于数据流做在线学习。

【传统在线算法，例如SGD】

在线学习算法的特点是：每来一个训练样本，就用该样本产生的loss和梯度对模型迭代一次，一个一个数据地进行训练，因此可以处理大数据量训练和在线训练。常用的有在线梯度下降（OGD）和随机梯度下降（SGD）等，本质思想是对上面【问题描述】中的未加和的单个数据的loss函数 L（w，zi)做梯度下降，因为每一步的方向并不是全局最优的，所以整体呈现出来的会是一个看似随机的下降路线。

梯度下降类的方法的优点是精度确实不错，但是不足相关paper主要提到两点：

1、简单的在线梯度下降很难产生真正稀疏的解，稀疏性在机器学习中是很看重的事情，尤其我们做工程应用，稀疏的特征会大大减少predict时的内存和复杂度。这一点其实很容易理解，说白了，即便加入L1范数，因为是浮点运算，训练出的w向量也很难出现绝对的零。到这里，大家可能会想说，那还不容易，当计算出的w对应维度的值很小时，我们就强制置为零不就稀疏了么。对的，其实不少人就是这么做的，FOBOS都是类似思想的应用；

2、对于不可微点的迭代会存在一些问题，具体有什么问题，有一篇paper是这么说的：the iterates of the subgradient method are very rarely at the points of non-differentiability。

————————————可恶的分割线———————————————————

—————————未经允许，禁止转载！——————————————————

Part 2：

SGD：

对正则项Ψ(w)的一般表示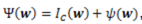：，其中，Ic(w)是一个hard集合约束，ψ(w)是一个soft正则化。
SGD的迭代形式：

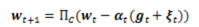其中，α_t是步长，g_t是loss function的次梯度，ξ_(t )是ψ(w)的次梯度（subgradient）， Π_C是对约束集C的投影。
对次梯度不熟的可以查看下wiki，主要用于处理函数的不可微点：
http://zh.wikipedia.org/wiki/%E6%AC%A1%E5%AF%BC%E6%95%B0") 0px 2px / cover; font-family: icomoon !important;">
SGD存在的问题上面主要列了1）精度低；2）收敛慢；3）几乎得不到稀疏解。其中对online learning最重要的问题是SGD很难得到需要的正则化设计的解，特别是几乎得不到稀疏解。

FOBOS：

FOBOS，2009年由Duchi（Berkeley）与Singer（google）[1]提出，对投影次梯度方法的一个改造。可以有效得到稀疏解。
投影次梯度方法的一般形式（与SGD几乎一致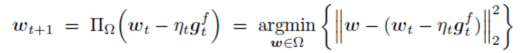）：FOBOS的迭代将投影次梯度法拆成两步：

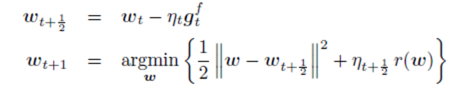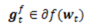其中，。第二步中，第一项保持新的解不要离第一步的临时解太远，第二项限制模型复杂度，即正则项，**用于产生稀疏解。** **为了得到后续统一的另一种表达，这里做个简单的推导：** 将迭代第一步带入第二步中，FOBOS的迭代等价于：
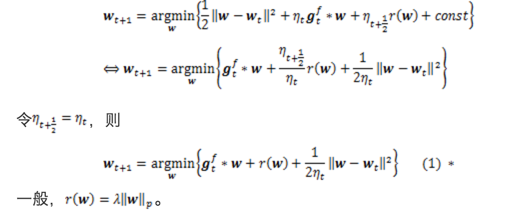注明：式（1）即为FOBOS的迭代形式，但是为何与总括表中第一行形式不同？而实际上两种方式是等价的！

RDA：

RDA，2010微软提出，特点：相对FOBOS，在精度与稀疏性之间做平衡，其中实验表明，在L1正则下，RDA比FOBOS可以更加有效地得到稀疏解。
RDA的迭代：收敛率与公式里的参数有关。式（2）经过简单的变化，可以得到总括表中的第三行。

————————————可恶的分割线———————————————————

—————————未经允许，禁止转载！——————————————————

Part 3：

首先感谢下H. Brendan McMahan搞了3年paper出来了，发展历程和基本说明如下：

10年理论性paper，但未显式地支持正则化项迭代；11年证明regret bound以及引入通用的正则化项；11年另一篇的paper揭示OGD、FOBOS、RDA等算法与FTRL关系；13年的paper给出了工程性实现，并且附带了详细的伪代码，开始被大规模应用。

可以看作RDA和FOBOS的混合，但在L1范数或者其他非光滑的正则项下，FTRL比前两者更加有效。

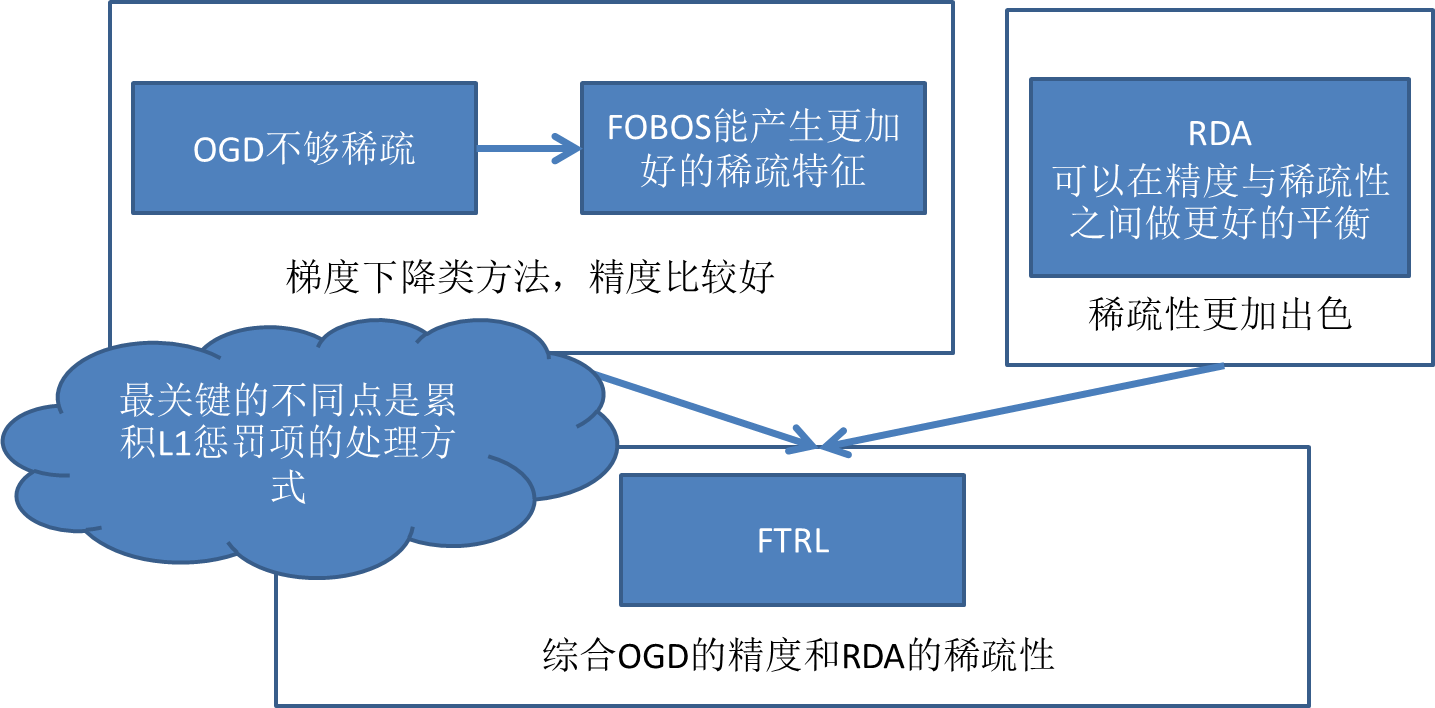
FTRL-Proximal，KDD 2013 google的论文，带工程实现伪代码，相信当前online learning的实现大都是参照这边paper来的。FTRL-Proximal，融合了RDA和FOBOS的特点，论文的实验对比，在L1正则下，稀疏性与精度都好于RDA和FOBOS。
FTRL，即Follow The Regularized Leader。FTRL-Proximal的形式上与RDA只有第三项不同，如下，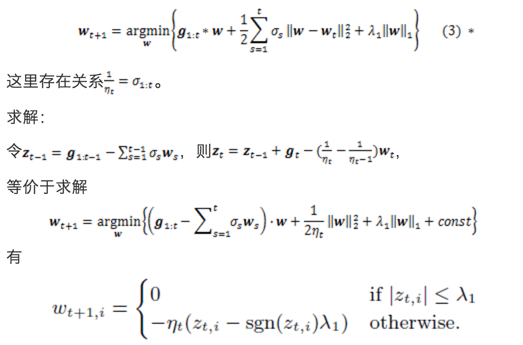
这一个closed form解推导并不难，w分3种情况求解就行了。论文（John Duchi and Yoram Singer. E_cient learning using forward-backward splitting. In NIPS, 2009.）中对于各种norm下的下一个点closed form的解有详细说明。

FTRL-Proximal对每次迭代的学习率做了一个优化，使得解的每一维的学习率不同，与统一的学习率相比，这种做法考虑了训练样本在不同特征维度分布的不均匀性。具体形式如下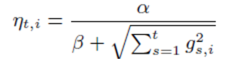FTRL-Proximal算法：伪码采用的是L1和L2混合正则，即实际的迭代是如下形式：

FTRL-Proximal算法的实现，基于式（4）。其中

， 是logistic regression的交叉熵loss function的梯度。

FTRL-Proximal工程实现上的tricks：

1.saving memory
方案1）Poisson Inclusion：对某一维度特征所来的训练样本，以p的概率接受并更新模型。
方案2）Bloom Filter Inclusion：用bloom filter从概率上做某一特征出现k次才更新。
2.浮点数重新编码
1）特征权重不需要用32bit或64bit的浮点数存储，存储浪费空间
2）16bit encoding，但是要注意处理rounding技术对regret带来的影响
3.训练若干相似model
1）对同一份训练数据序列，同时训练多个相似的model
2）这些model有各自独享的一些feature，也有一些共享的feature
3）出发点：有的特征维度可以是各个模型独享的，而有的各个模型共享的特征，可以用同样的数据训练。
4.Single Value Structure
1）多个model公用一个feature存储（例如放到cbase或redis中），各个model都更新这个共有的feature结构
2）对于某一个model，对于他所训练的特征向量的某一维，直接计算一个迭代结果并与旧值做一个平均
5.使用正负样本的数目来计算梯度的和（所有的model具有同样的N和P）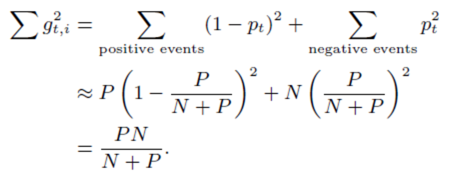
6.subsampling Training Data
1）在实际中，CTR远小于50%，所以正样本更加有价值。通过对训练数据集进行subsampling，可以大大减小训练数据集的大小
2）正样本全部采（至少有一个广告被点击的query数据），负样本使用一个比例r采样（完全没有广告被点击的query数据）。但是直接在这种采样上进行训练，会导致比较大的biased prediction
3）解决办法：训练的时候，对样本再乘一个权重。权重直接乘到loss上面，从而梯度也会乘以这个权重。

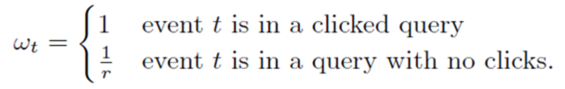
参考文献
[1] John Duchi and Yoram Singer. E_cient learning using forward-backward splitting. In NIPS, 2009.
[2] Lin Xiao. Dual averaging method for regularized stochastic learning and online optimization. In
NIPS, 2010.
[3] H. B. McMahan. Follow-the-regularized-leader and mirror descent: Equivalence theorems and L1 regularization. In AISTATS, 2011.
[4] H. Brendan McMahan, Gary Holt, D. Sculley, Michael Young,Dietmar Ebner, Julian Grady,LanNie, Todd Phillips, Eugene Davydov,Daniel Golovin, Sharat Chikkerur, Dan Liu, Martin Wattenberg,Arnar Mar Hrafnkelsson, Tom Boulos, Jeremy Kubica. Ad Click Prediction: a View from the Trenches. KDD’13, August 11–14, 2013, Chicago, Illinois, USA.