Manacher算法：求解最长回文字符串，时间复杂度为O(N)

原文转载自：http://blog.csdn.net/yzl_rex/article/details/7908259

回文串定义：“回文串”是一个正读和反读都一样的字符串，比如“level”或者“noon”等等就是回文串。回文子串，顾名思义，即字符串中满足回文性质的子串。

经常有一些题目围绕回文子串进行讨论，比如POJ3974最长回文，求最长回文子串的长度。朴素算法是依次以每一个字符为中心向两侧进行扩展，显然这个复杂度是O(N^2)的，关于字符串的题目常用的算法有KMP、后缀数组、AC 自动机，这道题目利用扩展KMP可以解答，其时间复杂度也很快O(N*logN)。

但是，今天笔者介绍一个专门针对回文子串的算法，其时间复杂度为O(n)，这就是manacher 算法。

大家都知道，求回文串时需要判断其奇偶性，也就是求aba 和abba 的算法略有差距。然而，这个算法做了一个简单的处理，很巧妙地把奇数长度回文串与偶数长度回文串统一考虑，也就是在每个相邻的字符之间插入一个分隔符，串的首尾也要加，当然这个分隔符不能再原串中出现，一般可以用‘#’或者‘$’等字符。例如：

原串：abaab

新串：#a#b#a#a#b#

这样一来，原来的奇数长度回文串还是奇数长度，偶数长度的也变成以‘#’为中心奇数回文串了。

算法的中心思想：

用一个辅助数组P 记录以每个字符为中心的最长回文半径，也就是P[i]记录以Str[i]字符为中心的最长回文串半径。P[i]最小为1，此时回文串为Str[i]本身。

我们可以对上述例子写出其P 数组，如下

新串： # a # b # a # a # b #

P[] : 1 2 1 4 1 2 5 2 1 2 1

我们可以证明P[i]-1 就是以Str[i]为中心的回文串在原串当中的长度。

证明：

1、显然L=2*P[i]-1 即为新串中以Str[i]为中心最长回文串长度。

2、以Str[i]为中心的回文串一定是以#开头和结尾的，例如“#b#b#”或“#b#a#b#”所以L 减去最前或者最后的‘#’字符就是原串中长度 的二倍，即原串长度为(L-1)/2，化简的P[i]-1。得证。

依次从前往后求得P 数组就可以了，这里用到了DP(动态规划)的思想， 也就是求P[i] 的时候，前面的P[]值已经得到了，我们利用回文串的特殊性质可以进行一个大大的优化。

先把核心代码贴上：

   for (i = 0; i < len; i++){
             if (maxid > i){
                 p[i] = min(p[2*id - i], maxid - i);
             }
             else{
                  p[i] = 1;
             }
             while (newstr[i+p[i]] == newstr[i-p[i]])
                    p[i]++;
             if (p[i] + i > maxid){
                 maxid = p[i] + i;
                 id = i;
             }
             if (ans < p[i])
                 ans = p[i];
         }  

为了防止求P[i]向两边扩展时可能数组越界，我们需要在数组最前面和最后面加一个特殊字符，令P[0]=‘$’最后位置默认为‘\0’不需要特殊处理。此外，我们用MaxId 变量记录在求i 之前的回文串中，延伸至最右端的位置，同时用id 记录取这个MaxId 的id 值。通过下面这句话，算法避免了很多没必要的重复匹配。

    if (maxid > i){
                 p[i] = min(p[2*id - i], maxid - i);
             }  

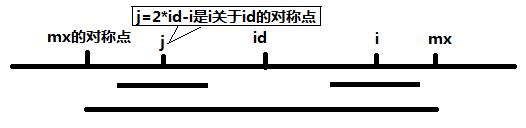
那么这句话是怎么得来的呢，其实就是利用了回文串的对称性，如下图，

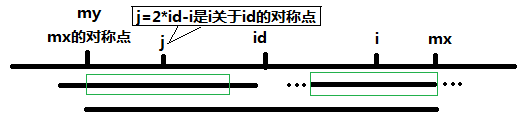
j=2*id-1 即为i 关于id 的对称点，根据对称性，P[j]的回文串也是可以对称到i 这边的,但是如果P[j]的回文串对称过来以后超过MaxId 的话，超出部分就不能对称过来了，如下图，

所以这里P[i]为的下限为两者中的较小者，p[i]=Min(p[2*id-i],MaxId-i)。算法的有效比较次数为MaxId 次，所以说这个算法的时间复杂度为O(n)。

下面就贴一个具体代码，求解最长回文字符串的代码：

 #include <iostream>
    #include <algorithm>
    #include <string>
    using namespace std;
    const int MAX = 100001;
    int len, p[2*MAX];
    char str[2*MAX], newstr[2*MAX];  
    void change()
    {
         int i;
         newstr[0] = '@';
         newstr[1] = '#';
         for (i = 0; i < len; i++){
             newstr[2*i + 2] = str[i];
             newstr[2*i + 3] = '#';
         }
         newstr[2*len + 2] = '\0';
         return ;
    }  
    void Manacher()
    {
         int i, j, id, maxid = 0, ans = 1;
         len = 2 * len + 2;
         for (i = 0; i < len; i++){
             if (maxid > i){
                 p[i] = min(p[2*id - i], maxid - i);
             }
             else{
                  p[i] = 1;
             }
             while (newstr[i+p[i]] == newstr[i-p[i]])
                    p[i]++;
             if (p[i] + i > maxid){
                 maxid = p[i] + i;
                 id = i;
             }
             if (ans < p[i])
                 ans = p[i];
         }  
         for (i = id, j = 0; i < id + ans; i++){
              if (newstr[i] != '#'){
                  str[j] = newstr[i];
                  j++;
              }
         }
         str[id+ans] = '\0';
         cout << ans - 1 << " " << str << endl;
         return ;
    }  
    int main()
    {
        while (scanf("%s", &str)){
              if (strcmp(str, "END") == 0)   break;
              len = strlen(str);
              change();
              Manacher();
        }  
        system("pause");
    }