【BZOJ2401】陶陶的难题I 欧拉函数+线性筛

【BZOJ2401】陶陶的难题I

题意：求，n<=1000000,T<=100000

题解：直接做是n*sqrt(n)的，显然会TLE，不过这题a和b都是循环到n，那么就可以进行如下的神奇变换：

$\sum\limits_{i=1}^n\sum\limits_{j=1}^nlcm(i,j)=2*\sum\limits_{i=1}^n\sum\limits_{j=1}^ilcm(i,j)-\sum\limits_{i=1}^ni$

是不是很神奇？然后继续推即可。

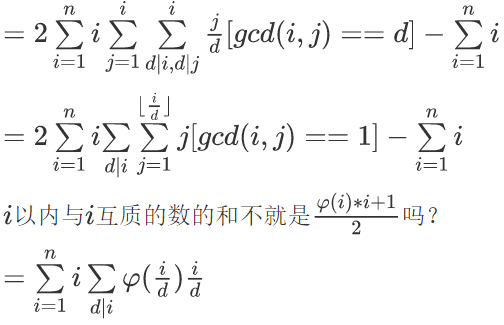
设$f(i)=\sum\limits_{d|i}\varphi({i\over d}){i\over d}$，我们只需要现行筛出f即可。

我们依旧只考虑i是质数的情况，当i=p时，$f(i)=p^2-p+1$，当i=p^2时，$f(i)=p^4-p^3+p^2-p+1$，以此类推。

所以我们维护一下x的最小质因子出现的次数，然后线性筛即可。

还有，因为出题人丧病，此题爆long long。

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
typedef long long ll;
const int N=1000000;
const ll P=1000000000000ll;
ll a,b;
int n,num,T;
int np[N+10],pri[N/10],phi[N+10];
ll g[N+10],h[N+10];
struct lll
{
	ll a,b;
	lll() {a=b=0;}
	lll(ll c)	{a=c/P,b=c%P;}
	lll(ll x,ll y){a=x,b=y;}
	lll operator + (const lll &x) const
	{
		lll y(a+x.a,b+x.b);
		y.a+=y.b/P,y.b%=P;
		return y;
	}
	lll operator - (const lll &x) const
	{
		lll y(a-x.a,b-x.b);
		if(y.b<0)	y.a--,y.b+=P;
		return y;
	}
	void print()
	{
		if(a)	printf("%lld%012lld\n",a,b);
		else	printf("%lld\n",b);
	}
}f[N+10];
inline ll rd()
{
	ll ret=0,f=1;	char gc=getchar();
	while(gc<'0'||gc>'9')	{if(gc=='-')f=-f;	gc=getchar();}
	while(gc>='0'&&gc<='9')	ret=ret*10+gc-'0',gc=getchar();
	return ret*f;
}
int main()
{
	int i,j,p;
	g[1]=1;
	for(i=2;i<=N;i++)
	{
		if(!np[i])	pri[++num]=i,g[i]=h[i]=(ll)i*i-i+1;
		for(j=1;j<=num&&i*pri[j]<=N;j++)
		{
			p=pri[j],np[i*p]=1;
			if(i%p==0)
			{
				h[i*p]=h[i]*p*p-p+1;
				g[i*p]=g[i]/h[i]*h[i*p];
				break;
			}
			h[i*p]=(ll)p*p-p+1;
			g[i*p]=g[i]*h[i*p];
		}
	}
	for(i=1;i<=N;i++)	f[i]=lll(g[i]*i)+f[i-1];
	T=rd();
	while(T--)
	{
		ll n=rd();
		lll ans=f[n];
		ans.print();
	}
	return 0;
}