ACM学习历程—POJ3565 Ants（最佳匹配KM算法）

Young naturalist Bill studies ants in school. His ants feed on plant-louses that live on apple trees. Each ant colony needs its own apple tree to feed itself.

Bill has a map with coordinates of n ant colonies and n apple trees. He knows that ants travel from their colony to their feeding places and back using chemically tagged routes. The routes cannot intersect each other or ants will get confused and get to the wrong colony or tree, thus spurring a war between colonies.

Bill would like to connect each ant colony to a single apple tree so that all n routes are non-intersecting straight lines. In this problem such connection is always possible. Your task is to write a program that finds such connection.

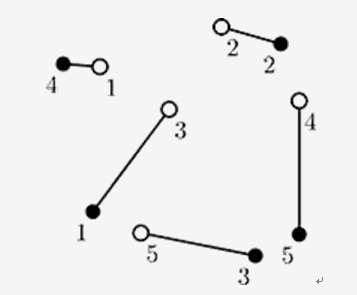
On this picture ant colonies are denoted by empty circles and apple trees are denoted by filled circles. One possible connection is denoted by lines.

Input

The first line of the input file contains a single integer number n (1 ≤ n ≤ 100) — the number of ant colonies and apple trees. It is followed by n lines describing n ant colonies, followed by n lines describing n apple trees. Each ant colony and apple tree is described by a pair of integer coordinates x and y (−10 000 ≤ x, y ≤ 10 000) on a Cartesian plane. All ant colonies and apple trees occupy distinct points on a plane. No three points are on the same line.

Output

Write to the output file n lines with one integer number on each line. The number written on i-th line denotes the number (from 1 to n) of the apple tree that is connected to the i-th ant colony.

Sample Input

5

-42 58

44 86

7 28

99 34

-13 -59

-47 -44

86 74

68 -75

-68 60

99 -60

Sample Output

4

2

1

5

3

题目就是求类似图中实心到空心圆的连线，一一映射，使两两线段不相交。

有一种思路就是一开始让所有点对随意连接，然后让相交的线段进行调整，这里比较好理解，比如AC与BD相交，那么AD与BC就必然不相交了。这样的话需要的调整的次数似乎不是很好计算。

但是可以肯定的是，最终状态必然是两两不相交了。

可以发现上面相交的AC与BD，必然满足AD+BC < AC+BD。这里可以用两次三角形两边之和大于第三边进行证明。这一步让点对里面边的权值和变小了。

于是考虑，逆命题:是否当边AC与BD可以减小成AD与BC时，一定是相交的？

事实证明这个命题是不一定的，但是可以发现当可以减小成AD与BC时，AD和BC一定是不相交的。否则会导致AD+BC > AC+BD。

所以只要能减小边权的和，一定能保证不相交。那么最终状态就变成了边权和最小的状态，也就是最小匹配。可以采用KM算法进行。

似乎是数据问题，不能使用边的平方进行处理。要用double保存边的大小，然后等于0的判断，改成小于eps。

代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <set>
#include <map>
#include <queue>
#include <string>
#define LL long long

using namespace std;

const int maxN = ;
const double inf = 1e10;
int n;
struct Point
{
    double x, y;
}x[maxN], y[maxN];
int nx, ny;
int link[maxN];
double lx[maxN], ly[maxN], slack[maxN], w[maxN][maxN];//link表示和y相接的x值，lx,ly为顶标，nx,ny分别为x点集y点集的个数
bool visx[maxN], visy[maxN];

inline double dis(int i, int j)
{
    double ans = (x[i].x-y[j].x)*(x[i].x-y[j].x) + (x[i].y-y[j].y)*(x[i].y-y[j].y);
    return -sqrt(ans);
}

bool DFS(int x)
{
    visx[x] = true;
    for (int y = ; y <= ny; y++)
    {
        if (visy[y])
            continue;
        double t = lx[x]+ly[y]-w[x][y];
        if (fabs(t) < 1e-)
        {
            visy[y] = true;
            if (link[y] == - || DFS(link[y]))
            {
                link[y] = x;
                return true;
            }
        }
        else if (slack[y] > t)//不在相等子图中slack取最小的
            slack[y] = t;
    }
    return false;
}

void KM()
{
    memset(link, -, sizeof(link));
    memset(ly, , sizeof(ly));
    for (int i = ; i <= nx; i++)//lx初始化为与它关联边中最大的
        for (int j = ; j <= ny; j++)
            if (j ==  || w[i][j] > lx[i])
                lx[i] = w[i][j];

    for (int x = ; x <= nx; x++)
    {
        for (int i = ; i <= ny; i++)
            slack[i] = inf;
        for (;;)
        {
            memset(visx, false, sizeof(visx));
            memset(visy, false, sizeof(visy));
            if (DFS(x))//若成功（找到了增广轨），则该点增广完成，进入下一个点的增广
                break;//若失败（没有找到增广轨），则需要改变一些点的标号，使得图中可行边的数量增加。
                    //方法为：将所有在增广轨中（就是在增广过程中遍历到）的X方点的标号全部减去一个常数d，
                    //所有在增广轨中的Y方点的标号全部加上一个常数d
            double d = inf;
            for (int i = ; i <= ny; i++)
                if (!visy[i] && d > slack[i])
                    d = slack[i];
            for (int i = ; i <= nx; i++)
                if (visx[i])
                    lx[i] -= d;
            for (int i = ; i <= ny; i++)//修改顶标后，要把所有不在交错树中的Y顶点的slack值都减去d
                if (visy[i])
                    ly[i] += d;
                else
                    slack[i] -= d;
        }
    }

    for (int i = ; i <= n; ++i)
        printf("%d\n", link[i]);
}

void input()
{
    nx = ny = n;
    for (int i = ; i <= n; ++i)
        scanf("%lf%lf", &y[i].x, &y[i].y);
    for (int i = ; i <= n; ++i)
        scanf("%lf%lf", &x[i].x, &x[i].y);
    for (int i = ; i <= n; ++i)
        for (int j = ; j <= n; ++j)
            w[i][j] = dis(i, j);
}

int main ()
{
    //freopen("test.in", "r", stdin);
    while (scanf ("%d", &n) != EOF)
    {
        input();
        KM();
    }
    return ;
}