HDU 1054树形DP入门

Strategic Game

Time Limit: 20000/10000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 9631    Accepted Submission(s): 4492

Problem Description

Bob enjoys playing computer games, especially strategic games, but sometimes he cannot find the solution fast enough and then he is very sad. Now he has the following problem. He must defend a medieval city, the roads of which form a tree. He has to put the minimum number of soldiers on the nodes so that they can observe all the edges. Can you help him?

Your program should find the minimum number of soldiers that Bob has to put for a given tree.

The input file contains several data sets in text format. Each data set represents a tree with the following description:

the number of nodes
the description of each node in the following format
node_identifier:(number_of_roads) node_identifier1 node_identifier2 ... node_identifier
or
node_identifier:(0)

The node identifiers are integer numbers between 0 and n-1, for n nodes (0 < n <= 1500). Every edge appears only once in the input data.

For example for the tree:

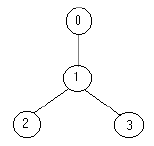
the solution is one soldier ( at the node 1).

The output should be printed on the standard output. For each given input data set, print one integer number in a single line that gives the result (the minimum number of soldiers). An example is given in the following table:

 

Sample Input

4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)

 

Sample Output

1
2

 

 

题意：求最少多少个点可以覆盖这一整颗树，每个点可以覆盖他的父亲节点和子节点

题解：如果父亲结点没放哨兵，那么子结点肯定要放置哨兵，如果父亲放置了哨兵，那么子结点可以考虑放或者不放。 并且存在兄弟节点的情况，

　　　每次处理完当前节点后就去处理兄弟节点，如此我们就可以用一个dp[maxn][2]的数组来存储当前的状态

　　　dp[node][1]+=min(dp[f][0],dp[f][1]);

代码如下：

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int maxn = ;
int f[maxn];
int son[maxn];
int bro[maxn];
int dp[maxn][];
int vis[maxn];
void dfs(int node){
  dp[node][]=;
  dp[node][]=;
  int f=son[node];
  while(f!=-){
    dfs(f);
    dp[node][]+=min(dp[f][],dp[f][]);
    dp[node][]+=dp[f][];
    f=bro[f];
  }
}
int main(){
  int n;
  while(cin>>n){
    int root=;
    memset(vis,,sizeof(vis));
    memset(son,-,sizeof(son));
    memset(f,,sizeof(f));
        for(int i=;i<n;i++)  {
            int num,cnt;
            scanf("%d:(%d)",&num,&cnt);
            for(int j=;j<cnt;j++)
            {
              int num1;
                cin>>num1;
                bro[num1] = son[num]; //同一个父节点的上一个兄弟
                son[num] = num1; //num的儿子是num1
                f[num1] = ; //num1是有父亲的,为下面找根结点做准备
            }
        }
        for(int i=;i<n;i++)
        {
            if(!f[i])  //如果没有父亲就可以做为根结点
            {
                root = i;
                break;
            }
        }
    dfs(root);
    cout<<min(dp[root][],dp[root][])<<endl;
  }
}