最小生成树问题(Kruskal 算法)(克鲁斯卡尔)
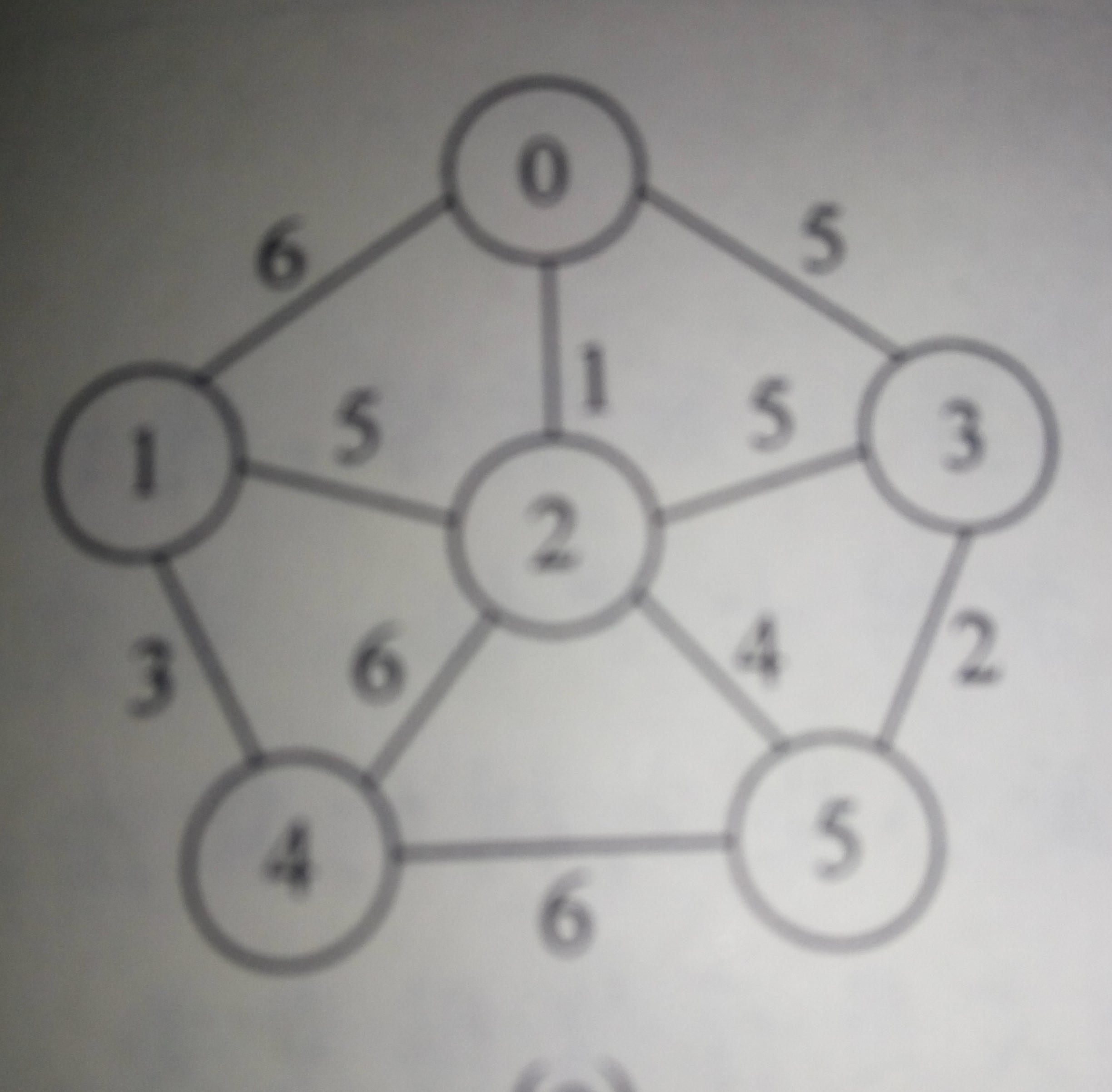
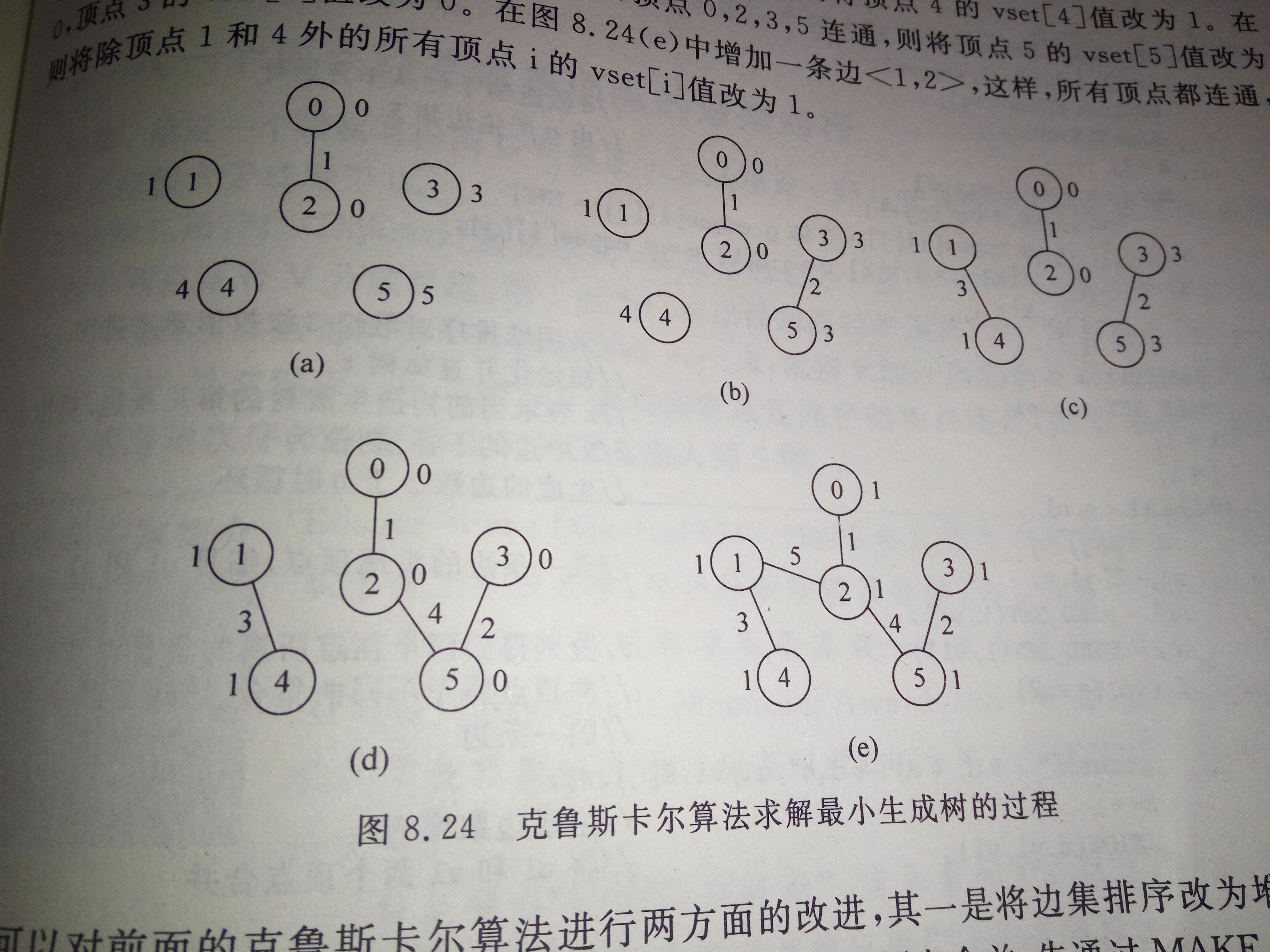
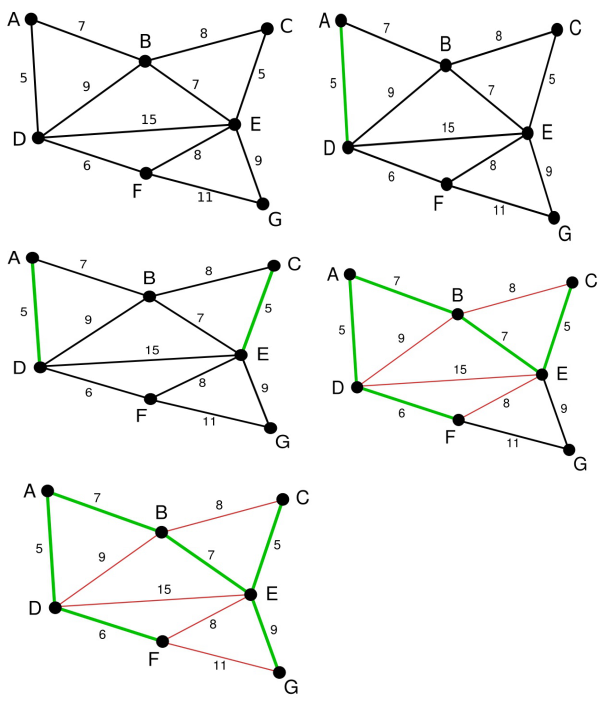



最小生成树问题(Kruskal 算法)(克鲁斯卡尔)的更多相关文章
- [模板] Kruskal算法 && 克鲁斯卡尔重构树
克鲁斯卡尔重构树 发现没把板子放上来... 现在放一下 克鲁斯卡尔算法的正确性是利用反证法证明的. 简要地说, 就是如果不加入当前权值最小的边 \(e_1\), 那么之后加入的边和这条边会形成一个环. ...
- Kruskal算法 克鲁斯卡尔
30行 #include <iostream> #include <algorithm> using namespace std; int f[5001],n,m,ans=0, ...
- 最小生成树——Kruskal(克鲁斯卡尔)算法
[0]README 0.1) 本文总结于 数据结构与算法分析, 源代码均为原创, 旨在 理解 Kruskal(克鲁斯卡尔)算法 的idea 并用 源代码加以实现: 0.2)最小生成树的基础知识,参见 ...
- 数据结构与算法——克鲁斯卡尔(Kruskal)算法
目录 应用场景-公交站问题 克鲁斯卡尔算法介绍 克鲁斯卡尔算法图解 克鲁斯卡尔算法分析 如何判断回路? 代码实现 无向图构建 克鲁斯卡尔算法实现 获取一个点的终点解释 应用场景-公交站问题 某城市新增 ...
- 最小生成树问题---Prim算法与Kruskal算法实现(MATLAB语言实现)
2015-12-17晚,复习,甚是无聊,阅<复杂网络算法与应用>一书,得知最小生成树问题(Minimum spanning tree)问题.记之. 何为树:连通且不含圈的图称为树. 图T= ...
- 最小生成树问题------------Prim算法(TjuOj_1924_Jungle Roads)
遇到一道题,简单说就是找一个图的最小生成树,大概有两种常用的算法:Prim算法和Kruskal算法.这里先介绍Prim.随后贴出1924的算法实现代码. Prim算法 1.概览 普里姆算法(Prim算 ...
- 最小生成树问题---Prim算法学习
一个具有n个节点的连通图的生成树是原图的最小连通子集,它包含了n个节点和n-1条边.若砍去任一条边,则生成树变为非连通图:若增加一条边,则在图中形成一条回路.本文所写的是一个带权的无向连通图中寻求各边 ...
- Prim算法和Kruskal算法介绍
一.Prim算法 普利姆(Prim)算法适用于求解无向图中的最小生成树(Minimum Cost Spanning Tree).下面是Prim算法构造最小生成树的过程图解. ...
- 最小生成树,Prim算法与Kruskal算法,408方向,思路与实现分析
最小生成树,Prim算法与Kruskal算法,408方向,思路与实现分析 最小生成树,老生常谈了,生活中也总会有各种各样的问题,在这里,我来带你一起分析一下这个算法的思路与实现的方式吧~~ 在考研中呢 ...
- 最小生成树之克鲁斯卡尔(Kruskal)算法
学习最小生成树算法之前我们先来了解下 下面这些概念: 树(Tree):如果一个无向连通图中不存在回路,则这种图称为树. 生成树 (Spanning Tree):无向连通图G的一个子图如果是一颗包含G的 ...
随机推荐
- 段落排版--缩进(text-indent)
中文文字中的段前习惯空两个文字的空白,这个特殊的样式可以用下面代码来实现: p{text-indent:2em;} <p>1922年的春天,一个想要成名名叫尼克卡拉威(托比?马奎尔Tobe ...
- WPF里面的常用笔刷
程序运行效果 <Window x:Class="This_brush.MainWindow" xmlns="http://schemas.microsoft.com ...
- jQuery实现页面元素智能定位
实现过程 Js侦听滚动事件,当页面滚动的距离(页面滚动的高度)超出了对象(要滚动的层)距离页面顶部的高度,即要滚动的层到达了浏览器窗口上边缘时,立即将对象定位属性position值改成fixed(固定 ...
- node http.get请求
var http = require('http'); var querystring = require('querystring') var url = 'http://www.baidu.com ...
- SGU 124.Broken line
时间限制:0.25s 空间限制:4M 题意: 给出n条线段和一个点,保证所有线段平行X轴或Y,并且闭合成一个多边形.判断这个点的位置是在多边形上,还是多边形内,还是多边形外. solution: 由于 ...
- OS X Yosemite下安装Hadoop2.5.1伪分布式环境
最近开始学习Hadoop,一直使用的是公司配好的环境.用了一段时间后发现对Hadoop还是一知半解,故决定动手在本机上安装一个供学习研究使用.正好自己用的是mac,所以没啥说的,直接安装. 总体流程 ...
- Android ListView+image的使用
首先创建layout部局文件xml: <?xml version="1.0" encoding="utf-8"?> <RelativeLayo ...
- excel poi 文件导出,支持多sheet、多列自动合并。
参考博客: http://www.oschina.net/code/snippet_565430_15074 增加了多sheet,多列的自动合并. 修改了部分过时方法和导出逻辑. 优化了标题,导出信息 ...
- dedecms 发布文章时,关键字会自动加内链
在后台找到:核心->批量维护->文档关键词维护 把关键字和链接网址删掉就可以了,生成更新后前端页面就不会再链接了.>_<.
- SQL语句 常用条件判断
条件判断写法: 对每天记录执行操作时,判断所限制的条件-----> 操作符: = <>(不匹配检查) != &l ...
