Aho_Corasick自动机（AC自动机）

首先，AC自动机不是Accept自动机，别以为把这段代码复制到OJ上就全都自动AC了……

其实这玩意是Aho-Corasick 造出来的，所以你懂的。

那么这玩意能干嘛咧？

•字符串的匹配问题

•多串的匹配问题※

看不懂吧？解释一下：

例如给几个单词 acbs，asf,dsef,再给出一个 很长的文章，acbsdfgeasf，问在这个文章中，总共出现了多少个单词，或者是单词出现的总次数。

怎么实现的呢，就是KMP+trie树。是以KMP为算法基础，trie为索引结构的东东。那它如何与kmp联系在一起？

•关键是在trie树上加了一种fail指针。

•Fail指针的用途：就像是kmp中的next的数组。

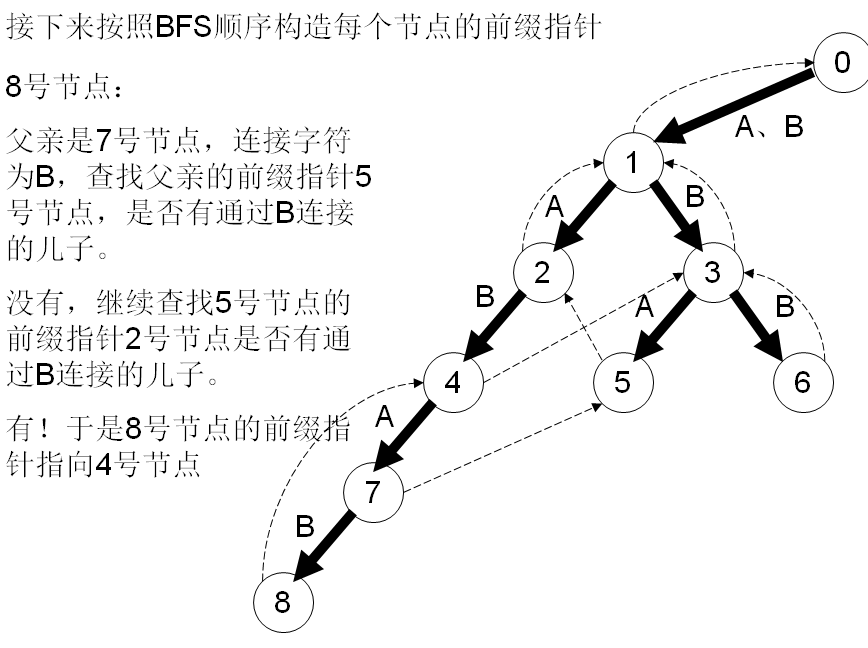
在字符串失配的时候确定转移的节点。AC难点就是指针的算法，看下面这么多图：

 

模板：

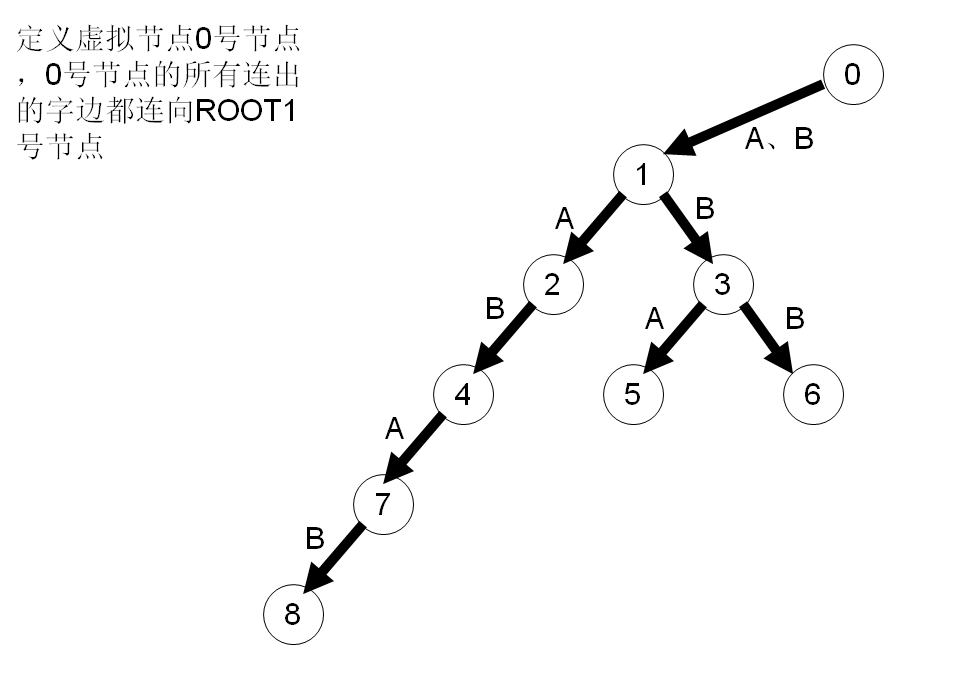
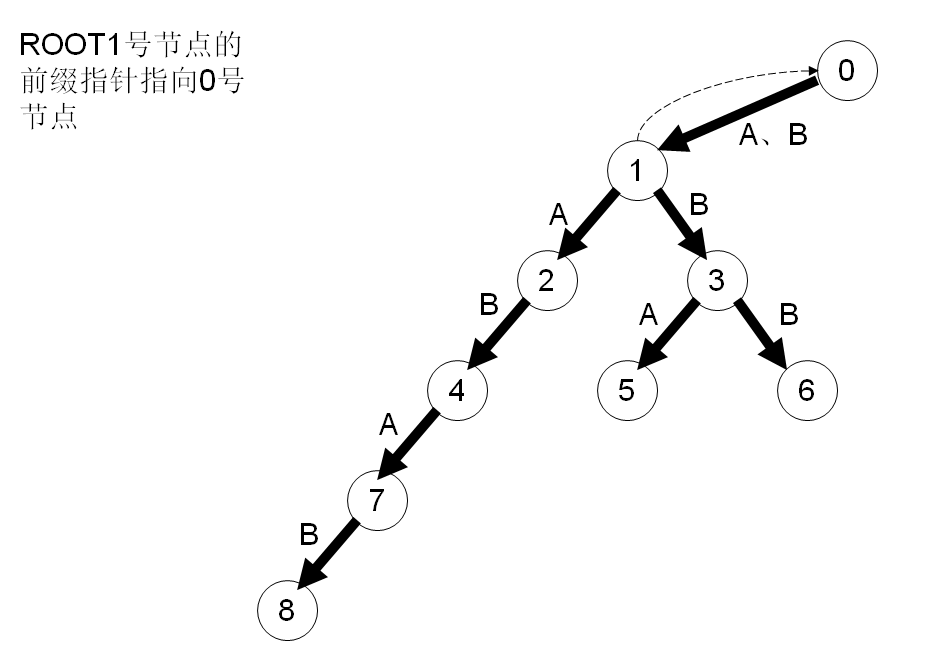
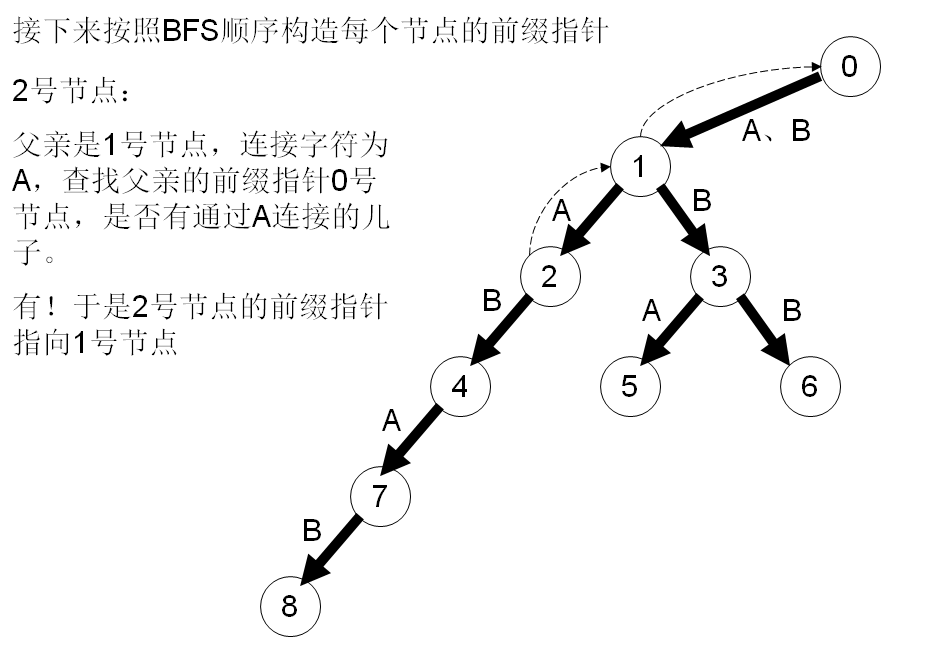
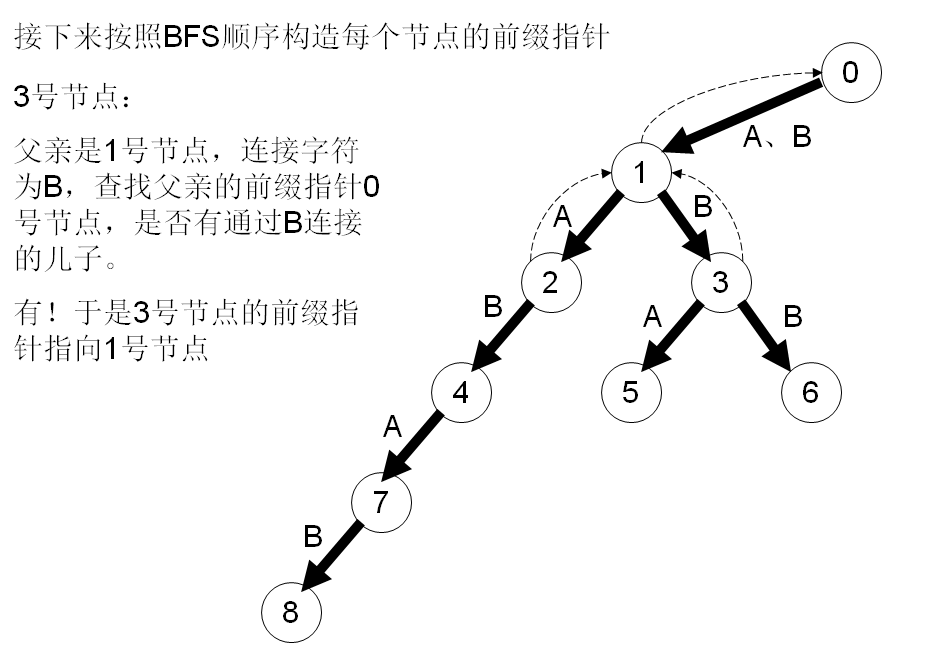
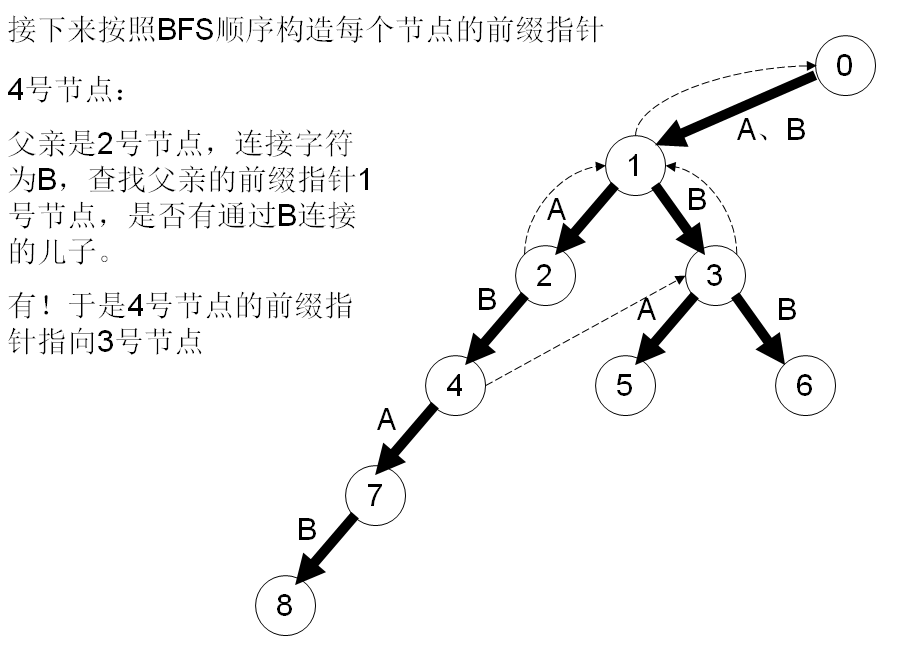
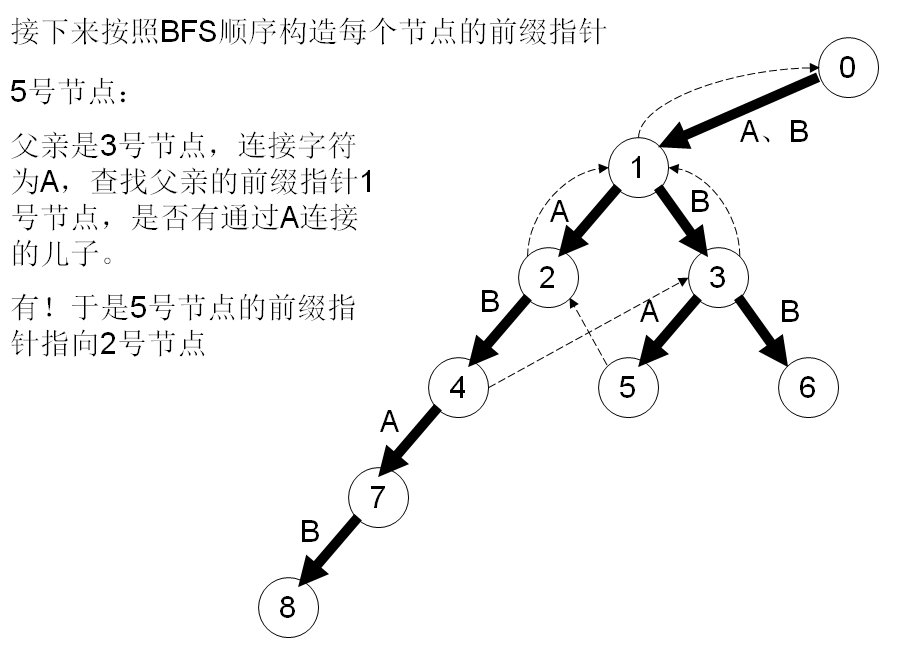
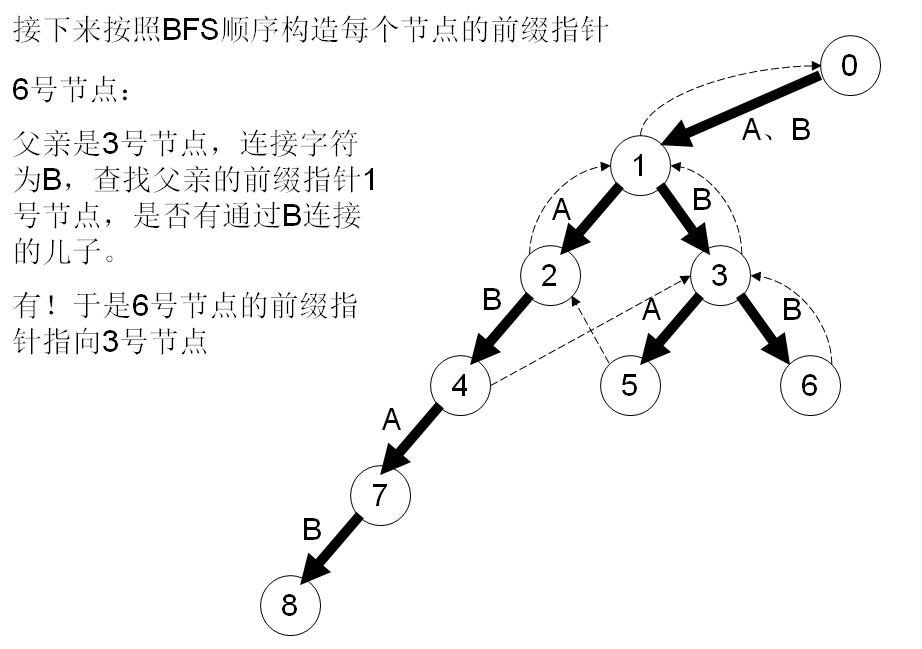
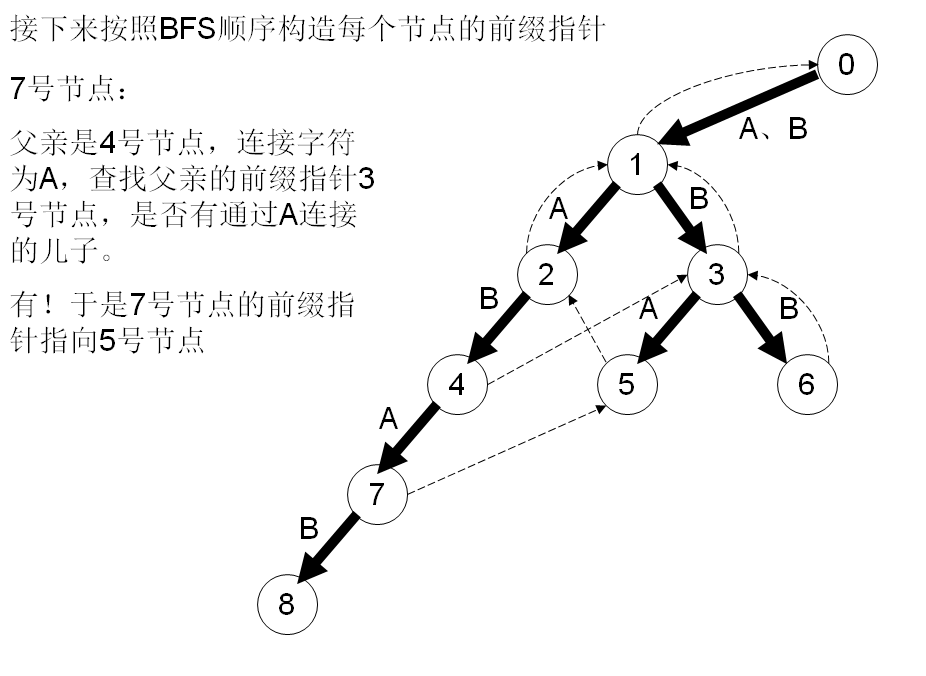
 #include <cstdio>
 #include <iostream>
 #include <algorithm>
 #include <cstring>
 #include <cmath>
 #include <queue>
 #define REP(i, s, n) for(int i = s; i <= n; i ++)
 #define RAP(i, n, s) for(int i = n; i >= s; i --)
 #define now ch[x][c]
 using namespace std;
 const int maxn =  + ;
 const int maxsig = ;
 char S[ + ];
 int n;
 inline void read(int &x){
     x = ; int sig = ; char ch = getchar();
     while(!isdigit(ch)) { if(ch == '-') sig = -; ch = getchar(); }
     while(isdigit(ch)) x =  * x + ch - '', ch = getchar();
     x *= sig; return ;
 }
 inline void write(int x){
     if(x == ) { putchar(''); return; }
     if(x < ) putchar('-'), x = -x;
     int len = , buf[];
     while(x) buf[len ++] = x % , x /= ;
     RAP(i, len - , ) putchar(buf[i] + ''); return ;
 }
 namespace Aho_Corasick{
     int ch[maxn][maxsig], val[maxn], f[maxn], last[maxn], len[maxn], ms;
     void AC_init(){
         ms = ;
         memset(ch, , sizeof(ch));
         memset(val, , sizeof(val));
         memset(f, , sizeof(f));
         memset(last, , sizeof(last));
         memset(len, , sizeof(len));
         return ;
     }
     void insert(char* s, int v){
         int x = , i;
         for(i = ; s[i] != '\0'; i ++){
             int c = s[i] - ''; if(!now) now = ++ ms; x = now;
         }
         val[x] = v; len[x] = i; return ;
     }
     void getfail(){
         queue<int> Q;
         REP(i, , maxsig - ) if(ch[][i]) Q.push(ch[][i]);
         while(!Q.empty()){
             int x = Q.front(); Q.pop();
             REP(c, , maxsig - ){
                 if(!now) { now = ch[f[x]][c]; continue; }
                 Q.push(now); int cur = f[x];
                 while(cur && !now) cur = f[cur];
                 f[now] = ch[cur][c]; last[now] = val[f[now]] ? f[now] : last[f[now]];
             }
         }
         return ;
     }
     void AC_print(int i, int j){
         if(j){
             write(val[j]); printf(": ");
             write(i - len[j] + ); printf(" to ");
             write(i); putchar('\n');
             AC_print(i, last[j]);
         }
         return ;
     }
     void solve(char* T){
         int cur = ;
         for(int i = ; T[i] != '\0'; i ++){
             cur = ch[cur][T[i] - ''];
             if(val[cur]) AC_print(i, cur);
             else if(last[cur]) AC_print(i, last[cur]);
         }
         return ;
     }
 }using namespace Aho_Corasick;
 bool init(){
     read(n); if(!n) return false;
     AC_init();
     REP(i, , n) scanf("%s", S), insert(S, i);
     return true;
 }
 void work(int cur){
     getfail();
     scanf("%s", S);
     printf("Case "); write(cur);
     printf(":\n");
     solve(S);
     return ;
 }
 void print(){

     return ;
 }
 int main(){
     int Case = ;
     while(init()) work(Case ++);
     return ;
 }