poj2826 An Easy Problem?!（计算几何）

传送门

•题意

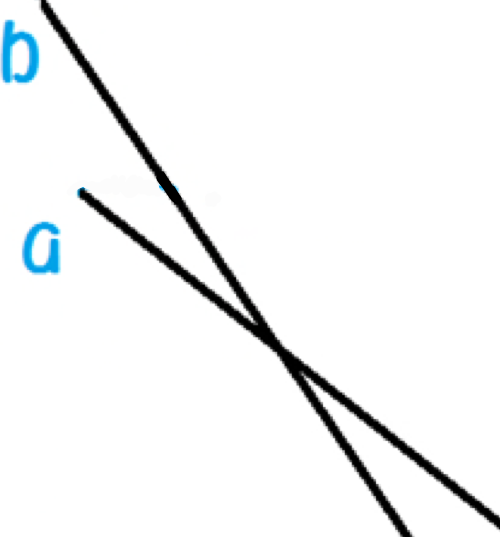
两根木块组成一个槽,给定两个木块的两个端点

雨水竖直下落，问槽里能装多少雨水,

•思路

找不能收集到雨水的情况

我们令线段较高的点为s点，较低的点为e点

①两条木块没有交点

②平行或重合

③至少有一条木块水平(雨水会滑落)

④形成覆盖，如"$\wedge $"，"人"，还有比较难想的上边长下边短的情况

• 其中形成"$\wedge$"型和"人"型 都是两条线段的交点比两条线段中较低的s点同高，

　　    也就是不大于较高的s点

• 上长下短的覆盖是两个s点都大于交点而不能存水的唯一情况

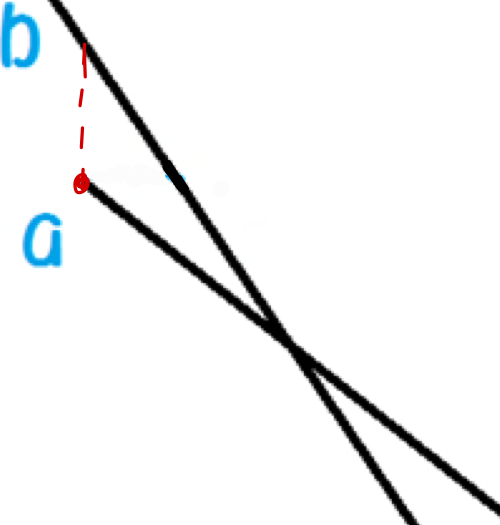
　　   如上图，我们可以在a.x出从b上引一条竖直线，看是否与a有交点，如果有说明覆盖了

能收集到雨水的情况要注意 水面与较低的s点水平

•代码

 //#include<bits/stdc++.h>
 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cmath>
 using namespace std;
 
 // `计算几何模板`
 const double eps = 1e-;
 const double inf = 1e20;
 const double pi = acos(-1.0);
 const int maxp = ;
 //`Compares a double to zero`
 int sgn(double x){
     if(fabs(x) < eps)return ;
     if(x < )return -;
     else return ;
 }
 //square of a double
 inline double sqr(double x){return x*x;}
 /*
  * Point
  * Point()               - Empty constructor
  * Point(double _x,double _y)  - constructor
  * input()             - double input
  * output()            - %.2f output
  * operator ==         - compares x and y
  * operator <          - compares first by x, then by y
  * operator -          - return new Point after subtracting curresponging x and y
  * operator ^          - cross product of 2d Points
  * operator *          - dot product
  * len()               - gives length from origin
  * len2()              - gives square of length from origin
  * distance(Point p)   - gives distance from p
  * operator + Point b  - returns new Point after adding curresponging x and y
  * operator * double k - returns new Point after multiplieing x and y by k
  * operator / double k - returns new Point after divideing x and y by k
  * rad(Point a,Point b)- returns the angle of Point a and Point b from this Point
  * trunc(double r)     - return Point that if truncated the distance from center to r
  * rotleft()           - returns 90 degree ccw rotated Point
  * rotright()          - returns 90 degree cw rotated Point
  * rotate(Point p,double angle) - returns Point after rotateing the Point centering at p by angle radian ccw
  */
 struct Point{
     double x,y;
     Point(){}
     Point(double _x,double _y){
         x = _x;
         y = _y;
     }
     void input(){
         scanf("%lf%lf",&x,&y);
     }
     void output(){
         printf("%.2f %.2f\n",x,y);
     }
     bool operator == (Point b)const{
         return sgn(x-b.x) ==  && sgn(y-b.y) == ;
     }
     bool operator < (Point b)const{
         return sgn(x-b.x)== ?sgn(y-b.y)<:x<b.x;
     }
     Point operator -(const Point &b)const{
         return Point(x-b.x,y-b.y);
     }
     //叉积
     double operator ^(const Point &b)const{
         return x*b.y - y*b.x;
     }
     //点积
     double operator *(const Point &b)const{
         return x*b.x + y*b.y;
     }
     //返回长度
     double len(){
         return hypot(x,y);//库函数
     }
     //返回长度的平方
     double len2(){
         return x*x + y*y;
     }
     //返回两点的距离
     double distance(Point p){
         return hypot(x-p.x,y-p.y);
     }
     Point operator +(const Point &b)const{
         return Point(x+b.x,y+b.y);
     }
     Point operator *(const double &k)const{
         return Point(x*k,y*k);
     }
     Point operator /(const double &k)const{
         return Point(x/k,y/k);
     }
     //`计算pa  和  pb 的夹角`
     //`就是求这个点看a,b 所成的夹角`
     //`测试 LightOJ1203`
     double rad(Point a,Point b){
         Point p = *this;
         return fabs(atan2( fabs((a-p)^(b-p)),(a-p)*(b-p) ));
     }
     //`化为长度为r的向量`
     Point trunc(double r){
         double l = len();
         if(!sgn(l))return *this;
         r /= l;
         return Point(x*r,y*r);
     }
     //`逆时针旋转90度`
     Point rotleft(){
         return Point(-y,x);
     }
     //`顺时针旋转90度`
     Point rotright(){
         return Point(y,-x);
     }
     //`绕着p点逆时针旋转angle`
     Point Rotate(Point p,double angle){
         Point v = (*this) - p;
         double c = cos(angle), s = sin(angle);
         return Point(p.x + v.x*c - v.y*s,p.y + v.x*s + v.y*c);
     }
 };
 /*
  * Stores two Points
  * Line()                         - Empty constructor
  * Line(Point _s,Point _e)        - Line through _s and _e
  * operator ==                    - checks if two Points are same
  * Line(Point p,double angle)     - one end p , another end at angle degree
  * Line(double a,double b,double c) - Line of equation ax + by + c = 0
  * input()                        - inputs s and e
  * adjust()                       - orders in such a way that s < e
  * length()                       - distance of se
  * angle()                        - return 0 <= angle < pi
  * relation(Point p)              - 3 if Point is on line
  *                                  1 if Point on the left of line
  *                                  2 if Point on the right of line
  * Pointonseg(double p)           - return true if Point on segment
  * parallel(Line v)               - return true if they are parallel
  * segcrossseg(Line v)            - returns 0 if does not intersect
  *                                  returns 1 if non-standard intersection
  *                                  returns 2 if intersects
  * linecrossseg(Line v)           - line and seg
  * linecrossline(Line v)          - 0 if parallel
  *                                  1 if coincides
  *                                  2 if intersects
  * crossPoint(Line v)             - returns intersection Point
  * disPointtoline(Point p)        - distance from Point p to the line
  * disPointtoseg(Point p)         - distance from p to the segment
  * dissegtoseg(Line v)            - distance of two segment
  * lineprog(Point p)              - returns projected Point p on se line
  * symmetryPoint(Point p)         - returns reflection Point of p over se
  *
  */
 struct Line{
     Point s,e;
     Line(){}
     Line(Point _s,Point _e){
         s = _s;
         e = _e;
     }
     bool operator ==(Line v){
         return (s == v.s)&&(e == v.e);
     }
     //`根据一个点和倾斜角angle确定直线,0<=angle<pi`
     Line(Point p,double angle){
         s = p;
         if(sgn(angle-pi/) == ){
             e = (s + Point(,));
         }
         else{
             e = (s + Point(,tan(angle)));
         }
     }
     //ax+by+c=0
     Line(double a,double b,double c){
         if(sgn(a) == ){
             s = Point(,-c/b);
             e = Point(,-c/b);
         }
         else if(sgn(b) == ){
             s = Point(-c/a,);
             e = Point(-c/a,);
         }
         else{
             s = Point(,-c/b);
             e = Point(,(-c-a)/b);
         }
     }
     void input(){
         s.input();
         e.input();
     }
     //根据x排序
     void adjustx(){
         if(e < s)swap(s,e);
     }
     //根据y排序
     void adjusty(){
         if(e.y>s.y) swap(s,e);
     }
     //求线段长度
     double length(){
         return s.distance(e);
     }
     //`返回直线倾斜角 0<=angle<pi`
     double angle(){
         double k = atan2(e.y-s.y,e.x-s.x);
         if(sgn(k) < )k += pi;
         if(sgn(k-pi) == )k -= pi;
         return k;
     }
     //`点和直线关系`
     //`1  在左侧`
     //`2  在右侧`
     //`3  在直线上`
     int relation(Point p){
         int c = sgn((p-s)^(e-s));
         if(c < )return ;
         else if(c > )return ;
         else return ;
     }
     // 点在线段上的判断
     bool Pointonseg(Point p){
         return sgn((p-s)^(e-s)) ==  && sgn((p-s)*(p-e)) <= ;
     }
     //`两向量平行(对应直线平行或重合)`
     bool parallel(Line v){
         return sgn((e-s)^(v.e-v.s)) == ;
     }
     //`两线段相交判断`
     //`2 规范相交`
     //`1 非规范相交`
     //`0 不相交`
     int segcrossseg(Line v){
         int d1 = sgn((e-s)^(v.s-s));
         int d2 = sgn((e-s)^(v.e-s));
         int d3 = sgn((v.e-v.s)^(s-v.s));
         int d4 = sgn((v.e-v.s)^(e-v.s));
         if( (d1^d2)==- && (d3^d4)==- )return ;
         return (d1== && sgn((v.s-s)*(v.s-e))<=) ||
             (d2== && sgn((v.e-s)*(v.e-e))<=) ||
             (d3== && sgn((s-v.s)*(s-v.e))<=) ||
             (d4== && sgn((e-v.s)*(e-v.e))<=);
     }
     //`直线和线段相交判断`
     //`-*this line   -v seg`
     //`2 规范相交`
     //`1 非规范相交`
     //`0 不相交`
     int linecrossseg(Line v){
         int d1 = sgn((e-s)^(v.s-s));
         int d2 = sgn((e-s)^(v.e-s));
         if((d1^d2)==-) return ;
         return (d1==||d2==);
     }
     //`两直线关系`
     //`0 平行`
     //`1 重合`
     //`2 相交`
     int linecrossline(Line v){
         if((*this).parallel(v))
             return v.relation(s)==;
         return ;
     }
     //`求两直线的交点`
     //`要保证两直线不平行或重合`
     Point crossPoint(Line v){
         double a1 = (v.e-v.s)^(s-v.s);
         double a2 = (v.e-v.s)^(e-v.s);
         return Point((s.x*a2-e.x*a1)/(a2-a1),(s.y*a2-e.y*a1)/(a2-a1));
     }
     //点到直线的距离
     double disPointtoline(Point p){
         return fabs((p-s)^(e-s))/length();
     }
     //点到线段的距离
     double disPointtoseg(Point p){
         if(sgn((p-s)*(e-s))< || sgn((p-e)*(s-e))<)
             return min(p.distance(s),p.distance(e));
         return disPointtoline(p);
     }
     //`返回线段到线段的距离`
     //`前提是两线段不相交，相交距离就是0了`
     double dissegtoseg(Line v){
         return min(min(disPointtoseg(v.s),disPointtoseg(v.e)),min(v.disPointtoseg(s),v.disPointtoseg(e)));
     }
     //`返回点p在直线上的投影`
     Point lineprog(Point p){
         return s + ( ((e-s)*((e-s)*(p-s)))/((e-s).len2()) );
     }
     //`返回点p关于直线的对称点`
     Point symmetryPoint(Point p){
         Point q = lineprog(p);
         return Point(*q.x-p.x,*q.y-p.y);
     }
     //求线段交点
     Point intersection(Line v)
     {
         double  a1,a2,b1,b2,c1,c2;
         a1=s.y-e.y;
         a2=v.s.y-v.e.y;
         b1=e.x-s.x;
         b2=v.e.x-v.s.x;
         c1=s.x*e.y-e.x*s.y;
         c2=v.s.x*v.e.y-v.e.x*v.s.y;
         return Point((c1*b2-c2*b1)/(a2*b1-a1*b2),(c1*a2-c2*a1)/(b2*a1-b1*a2));
     }
 };
 int main()
 {
     int t;
     scanf("%d",&t);
     while(t--)
     {
         double a,b,c,d;
         Line l1,l2,l3,l4;
         scanf("%lf%lf%lf%lf",&a,&b,&c,&d);
         l1=Line(Point(a,b),Point(c,d));
         scanf("%lf%lf%lf%lf",&a,&b,&c,&d);
         l2=Line(Point(a,b),Point(c,d));
         l1.adjusty(),l2.adjusty();
 
         double s=-;
         if(l1.parallel(l2))///平行或重合
             s=;
         else if((!l1.angle())||(!l2.angle()))///k=0
             s=;
         else if(l1.segcrossseg(l2)==)///不相交
             s=;
         else if(l1.segcrossseg(l2))///相交
         {
             Point P=l1.intersection(l2);///获得交点
             Point p1,p2;
             int flag=,flag1=;
             if(l1.s.y-P.y>eps) p1=l1.s,flag=;
             if(l2.s.y-P.y>eps) p2=l2.s,flag1=;
             if(flag&&flag1)
             {///还有一种情况没有水。上面的y把下面的y覆盖---遮挡判断
                 if(p1.y-p2.y>eps)
                 {
                     if(l1.segcrossseg(Line(p2,Point(p2.x,p1.y+2.0))))
                     {
                         printf("0.00\n");
                         continue;
                     }
                 }
                 if(p2.y-p1.y>eps)
                 {
                     if(l2.segcrossseg(Line(p1,Point(p1.x,p2.y+2.0))))
                     {
                         printf("0.00\n");
                         continue;
                     }
                 }
                 if(p1.y-p2.y>eps)
                 {
                     ///取p1.x的水平和p2.y,p1与p2.x的交点
                     ///水面和低处水平
                     double x=p1.x>?p1.x+1.00:p1.x-1.0;
                     p1=l1.intersection(Line(Point(x,p2.y),Point(-x,p2.y)));
                 }
                 else
                 {
                     double x=p2.x>?p2.x+1.00:p2.x-1.0;
                     p2=l2.intersection(Line(Point(x,p1.y),Point(-x,p1.y)));
                 }
                 s=fabs((p1.x-p2.x)*(p1.y-P.y)*0.5)+eps;
             }
             else
                 s=;
         }
         printf("%.2f\n",s);
     }
 }