（转）KL散度的理解

KL散度（KL divergence）

全称：Kullback-Leibler Divergence。

用途：比较两个概率分布的接近程度。
在统计应用中，我们经常需要用一个简单的，近似的概率分布 f * 来描述。

观察数据 D 或者另一个复杂的概率分布 f 。这个时候，我们需要一个量来衡量我们选择的近似分布 f * 相比原分布 f 究竟损失了多少信息量，这就是KL散度起作用的地方。

熵（entropy）

想要考察信息量的损失，就要先确定一个描述信息量的量纲。

在信息论这门学科中，一个很重要的目标就是量化描述数据中含有多少信息。

为此，提出了熵的概念，记作 H 。

一个概率分布所对应的熵表达如下：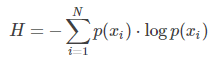

如果我们使用 log 2 作为底，熵可以被理解为：我们编码所有信息所需要的最小位数(minimum numbers of bits)。

需要注意的是：通过计算熵，我们可以知道信息编码需要的最小位数，却不能确定最佳的数据压缩策略。怎样选择最优数据压缩策略，使得数据存储位数与熵计算的位数相同，达到最优压缩，是另一个庞大的课题。

KL散度的计算

现在，我们能够量化数据中的信息量了，就可以来衡量近似分布带来的信息损失了。
KL散度的计算公式其实是熵计算公式的简单变形,在原有概率分布 p 上，加入我们的近似概率分布 q ，计算他们的每个取值对应对数的差：

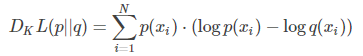
换句话说，KL散度计算的就是数据的原分布与近似分布的概率的对数差的期望值。

在对数以2为底时， log 2 ，可以理解为“我们损失了多少位的信息”。

写成期望形式：

更常见的是以下形式：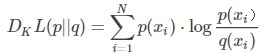

现在，我们就可以使用KL散度衡量我们选择的近似分布与数据原分布有多大差异了。

散度不是距离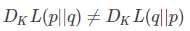

因为KL散度不具有交换性，所以不能理解为“距离”的概念，衡量的并不是两个分布在空间中的远近，更准确的理解还是衡量一个分布相比另一个分布的信息损失(infomation lost)。

使用KL散度进行优化

通过不断改变预估分布的参数，我们可以得到不同的KL散度的值。

在某个变化范围内，KL散度取到最小值的时候，对应的参数是我们想要的最优参数。

这就是使用KL散度优化的过程。

神经网络进行的工作很大程度上就是“函数的近似”(function approximators)。

因此我们可以使用神经网络学习很多复杂函数，学习过程的关键就是设定一个目标函数来衡量学习效果。

也就是通过最小化目标函数的损失来训练网络(minimizing the loss of the objective function)。

而KL散度可以作为正则化项(regularization term)加入损失函数之中，即使用KL散度来最小化我们近似分布时的信息损失，让我们的网络可以学习很多复杂的分布。

一个典型应用是VAE(变分自动编码)。

https://blog.csdn.net/ericcchen/article/details/72357411