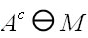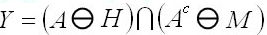C#数字图像处理（十四）击中击不中变换 (Hit-miss)

击中击不中变换定义

击中击不中变换(HMT)需要两个结构元素B₁和B₂,合成一个结构元素对B=(B₁,B₂)

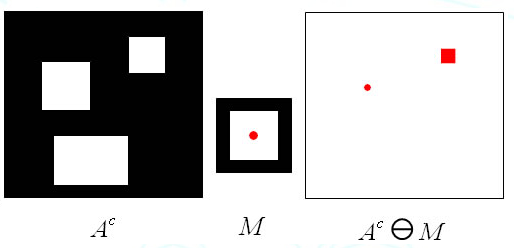
一个用于探测图像内部,作为击中部分;另一个用于探测图像外部,作为击不中部分。显然,B₁和B₂是不应该相连接的,即B₁∩B₂=Φ。击中击不中变换的数学表达式为：

g(x, y)=hitmiss[f(x, y), B]=erode[f(x, y), B₁]AND erode[f^c(x, y), B₂]

其中,f^c(x,y)表示的是f(x,y)的补集。

Hit-miss算法步骤：

击中击不中变换是形态学中用来检测特定形状所处位置的一个基本工具。它的原理就是使用腐蚀；如果要在一幅图像A上找到B形状的目标，我们要做的是：

首先，建立一个比B大的模板W；使用此模板对图像A进行腐蚀，得到图像假设为Process1;

其次，用B减去W，从而得到V模板(W-B)；使用V模板对图像A的补集进行腐蚀，得到图像假设为Process2;

然后，Process1与Process2取交集；得到的结果就是B的位置。这里的位置可能不是B的中心位置，要视W-B时对齐的位置而异；

其实很简单，两次腐蚀，然后交集，结果就出来了。

 

Hit-miss原理：

基于腐蚀运算的一个特性：腐蚀的过程相当于对可以填入结构元素的位置作标记的过程。

腐蚀中，虽然标记点取决于原点在结构元素中的相对位置，但输出图像的形状与此无关，改变原点的位置，只会导致输出结果发生平移。

既然腐蚀的过程相当于对可以填入结构元素的位置作标记的过程，可以利用腐蚀来确定目标的位置。进行目标检测，既要检测到目标的内部，也要检测到外部，即在一次运算中可以同时捕获内外标记。 

由于以上两点，采用两个结构基元H、M，作为一个结构元素对B＝（H，M），一个探测目标内部，一个探测目标外部。当且仅当H平移到某一点可填入X的内部，M平移到该点可填入X的外部时，该点才在击中击不中变换的输出中。

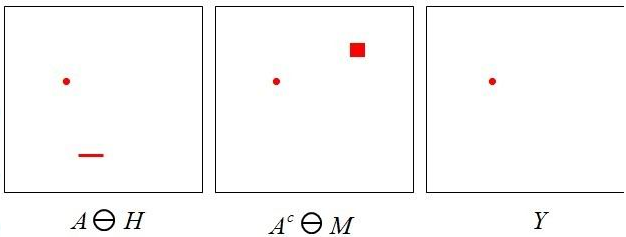
Hit-miss示意图：

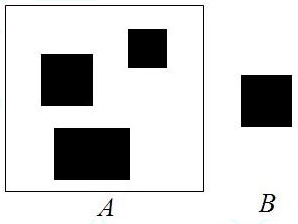
在A图中寻找B图所示的图像目标的位置。

解：

1、确定结构元素

既然是寻找图B所示形状，选取H为图B所示的形状。再选一个小窗口W，W包含H，M＝W－H。如下图所示：

2、求

3、求

4、求

        /// <summary>
        /// 击中击不中：只能处理位深度为8的512*512图像
        /// </summary>
        /// <param name="sender"></param>
        /// <param name="e"></param>
        private void hitMiss_Click(object sender, EventArgs e)
        {
            if (curBitmap != null)
            {
                hitmiss hitAndMiss = new hitmiss();
                if (hitAndMiss.ShowDialog() == DialogResult.OK)
                {
                    Rectangle rect = new Rectangle(, , curBitmap.Width, curBitmap.Height);
                    BitmapData bmpData = curBitmap.LockBits(rect,  ImageLockMode.ReadWrite, curBitmap.PixelFormat);
                    IntPtr ptr = bmpData.Scan0;
                    int bytes = curBitmap.Width * curBitmap.Height;
                    byte[] grayValues = new byte[bytes];
                    Marshal.Copy(ptr, grayValues, , bytes);

                    //得到击中结构元素
                    bool[] hitStru = hitAndMiss.GetHitStruction;
                    //得到击不中结构元素
                    bool[] missStru = hitAndMiss.GetMissStruction;

                    byte[] tempArray = new byte[bytes];
                    byte[] temp1Array = new byte[bytes];
                    byte[] temp2Array = new byte[bytes];
                    for (int i = ; i < bytes; i++)
                    {
                        //原图补集
                        tempArray[i] = (byte)( - grayValues[i]);
                        temp1Array[i] = ;
                        temp2Array[i] = ;
                    }

                    //应用击中结构元素进行腐蚀运算
                    for (int i = ; i < curBitmap.Height - ; i++)
                    {
                        for (int j = ; j < curBitmap.Width - ; j++)
                        {
                            //当前位置是黑色或者是击中结构元素的这一位置没有选中
                            if ((grayValues[(i - ) * curBitmap.Width + j - ] ==  || hitStru[] == false) &&
                                (grayValues[(i - ) * curBitmap.Width + j] ==  || hitStru[] == false) &&
                                (grayValues[(i - ) * curBitmap.Width + j + ] ==  || hitStru[] == false) &&
                                (grayValues[i * curBitmap.Width + j - ] ==  || hitStru[] == false) &&
                                (grayValues[i * curBitmap.Width + j] ==  || hitStru[] == false) &&
                                (grayValues[i * curBitmap.Width + j + ] ==  || hitStru[] == false) &&
                                (grayValues[(i + ) * curBitmap.Width + j - ] ==  || hitStru[] == false) &&
                                (grayValues[(i + ) * curBitmap.Width + j] ==  || hitStru[] == false) &&
                                (grayValues[(i + ) * curBitmap.Width + j + ] ==  || hitStru[] == false))
                            {
                                temp1Array[i * curBitmap.Width + j] = ;
                            }

                        }
                    }

                    //应用击不中结构元素进行腐蚀运算
                    for (int i = ; i < curBitmap.Height - ; i++)
                    {
                        for (int j = ; j < curBitmap.Width - ; j++)
                        {
                            ////当前位置是黑色或者是击不中结构元素的这一位置没有选中
                            if ((tempArray[(i - ) * curBitmap.Width + j - ] ==  || missStru[] == false) &&
                                (tempArray[(i - ) * curBitmap.Width + j] ==  || missStru[] == false) &&
                                (tempArray[(i - ) * curBitmap.Width + j + ] ==  || missStru[] == false) &&
                                (tempArray[i * curBitmap.Width + j - ] ==  || missStru[] == false) &&
                                (tempArray[i * curBitmap.Width + j] ==  || missStru[] == false) &&
                                (tempArray[i * curBitmap.Width + j + ] ==  || missStru[] == false) &&
                                (tempArray[(i + ) * curBitmap.Width + j - ] ==  || missStru[] == false) &&
                                (tempArray[(i + ) * curBitmap.Width + j] ==  || missStru[] == false) &&
                                (tempArray[(i + ) * curBitmap.Width + j + ] ==  || missStru[] == false))
                            {
                                temp2Array[i * curBitmap.Width + j] = ;
                            }

                        }
                    }

                    //两个腐蚀运算结果再进行“与”操作
                    for (int i = ; i < bytes; i++)
                    {
                        if (temp1Array[i] ==  && temp2Array[i] == )
                        {
                            tempArray[i] = ;
                        }
                        else
                        {
                            tempArray[i] = ;
                        }
                    }

                    grayValues = (byte[])tempArray.Clone();

                    Marshal.Copy(grayValues, , ptr, bytes);
                    curBitmap.UnlockBits(bmpData);
                }

                Invalidate();
            }
        }