动画 | 什么是平衡二分搜索树（AVL）？

二分搜索树又名有序二叉查找树，它有一个特点是左子树的节点值要小于父节点值，右子树的节点值要大于父节点值。基于这样的特点，我们在查找某个节点的时候，可以采取二分查找的思想快速找到这个节点，时间复杂度期望值是为O(log n)，但是它有最坏的的情况下。

例如，输入数组[9，7，5，3，1]，如果要满足二分搜索树的规则插入一个个节点，这样的二叉树会退化成一条线性表，待会查找元素的时候时间复杂度已达O(N)。

所以针对这种情况，我们引申出了平衡二分搜索树，它每个节点的左右子树高度差不会超过1，它能在O(log n)内完成插入、查找和删除操作。平衡二分搜索树种类比较多，AVL树是其中的一种，但是它是最早被发明的自平衡二分搜索树。

AVL树也会被称为高度平衡树，因为它比二分搜索树多了一个特点：任一节点的左右子树高度差最大为1。如果以后去参赛，可以根据数据的情况更改高度差最大值，甚至也可以制定高度差相差几倍。

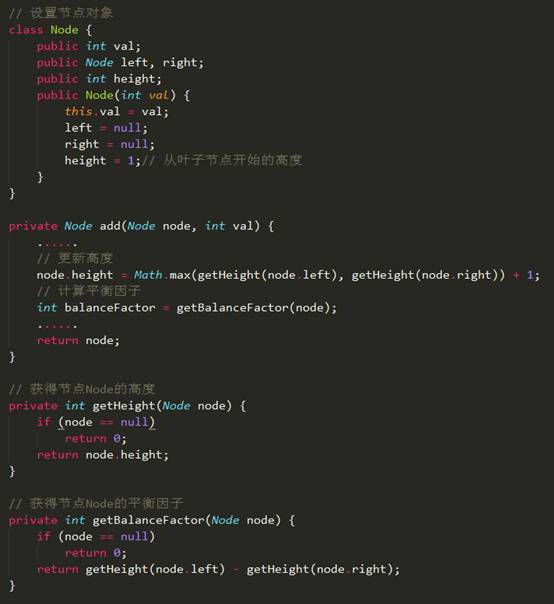
计算高度和平衡因子

计算高度是从叶子节点开始的，起始高度默认为1。然后计算叶子节点的父节点高度，比较左右子树的高度，采取最大值再加1就是这个节点的高度了。依此类推，直到整个树的顶点。

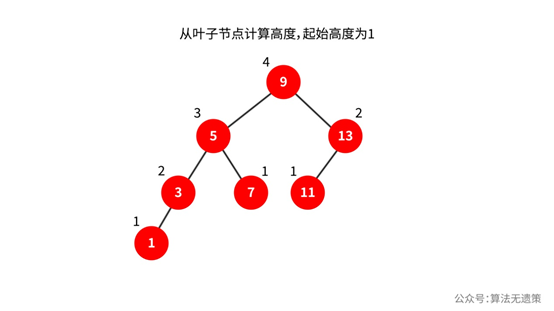
计算平衡因子也跟计算高度从叶子节点开始的，然后依次往父节点计算。节点的平衡因子公式是它左子树的高度减去它右子树的高度，有时候也会相反，可负数。

带有平衡因子-1、0或1的节点被认为是平衡的，即期望平衡节点的平衡因子的绝对值不会大于高度差最大值的。带有平衡因子-2或2的节点被认为是不平衡的，意味着需要重新调整这个树。平衡因子的绝对值最大值不会超过高度差最大值+1，说明这个数的任一节点的平衡因子不会出现-3或3。

如果改定高度差最大值为2，那么平衡因子会出现-3或3了，同时这个节点也是不平衡的，需要旋转调整。带有平衡因子-2、-1、0、1或2则被认为是平衡的。

动画

算法动画视频地址

Code

左旋转和右旋转

AVL树调整不平衡的节点分为左旋转和右旋转，却分四种情况：LL、RR、LR和RL。其中L是左旋转，R是右旋转。如何采取使用哪一种情况则看插入的节点在哪里。

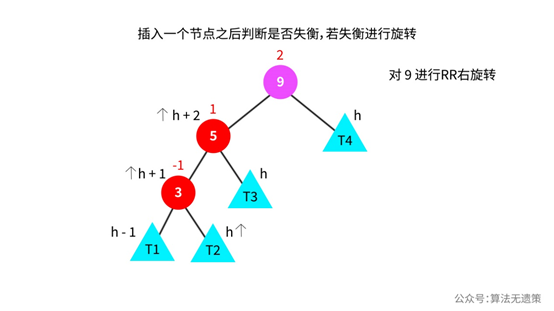
如果插入的节点是再T2子树里面，T1、T2、T3和T4都代表一个子树。T2里面插入一个节点，这个子树的高度加1，再计算父节点的平衡因子。如果这个节点是平衡的，则更新这个节点的高度。然后再往上计算父节点的平衡因子，接着判断是否平衡，如果是平衡的则更新高度，直到是不平衡的则进行旋转操作。

看上面图中，节点9是不平衡的，需要进行旋转操作。那如何进行哪种情况操作呢？

看左右子树哪一个子树插入了一个节点，节点5的左子树高度加1，导致节点5的平衡因子由0变成1。为了让节点5的平衡因子可以由1变成0，则希望节点5的右子树可以高度加1，所以就向节点5的父节点9进行右旋转操作，重新调整平衡因子，节点5的平衡因子恢复为0。

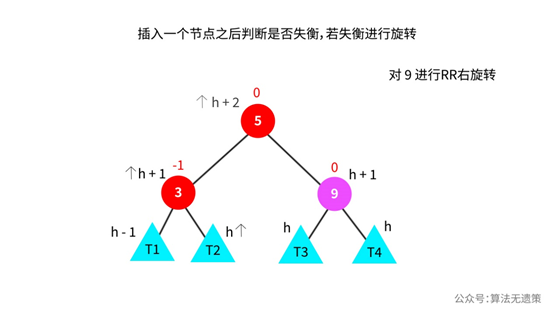
如果是下面情况，则不能单纯的进行右旋转操作了。看下面途中，插入一个节点是在节点3右子树发生的，节点3的平衡因子由0变成-1，应该希望是节点3左子树的高度可以高点。所以对节点3进行左旋转操作。

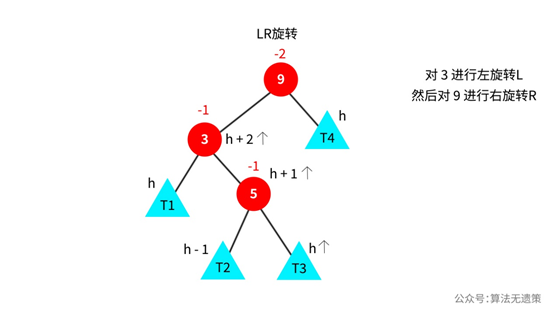
对节点3进行左旋转操作之后，更新相应节点的高度和平衡因子。看下面图中，发现节点5的平衡因子由-1变成1了，为了让1变成0，则希望是节点5的右子树高度可以高一点，所以对节点9进行右旋转操作。

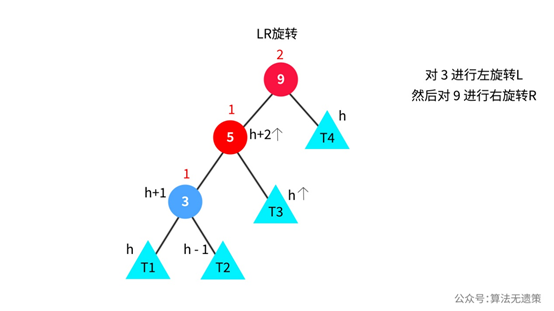
进行LR旋转的操作如下图，节点5的平衡因子已恢复为0，节点9由开始的不平衡已变成平衡。

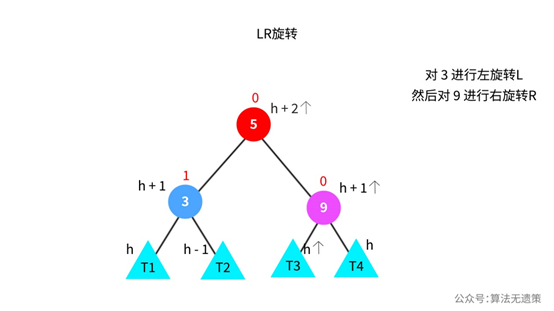
动画

算法动画视频地址

Code

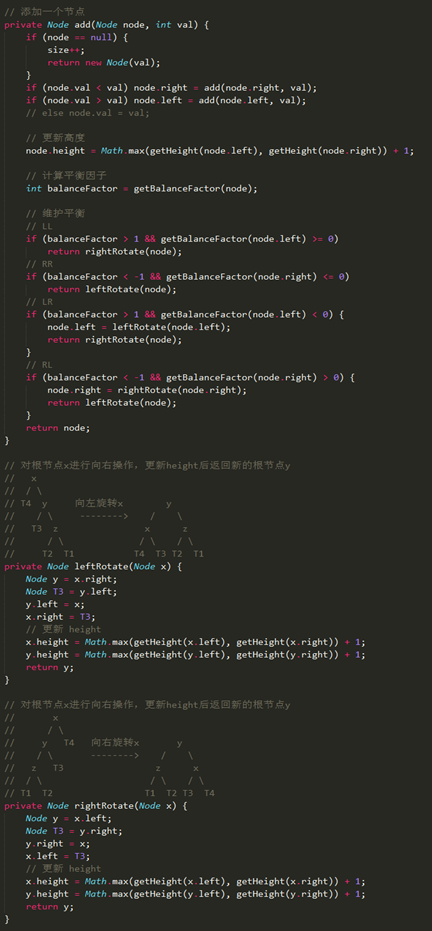
删除节点

AVL树的删除操作和二分搜索树一样，也分待删除结点的右子树为空、左子树为空和左右子树都不为空的情况。

那如何更新高度和平衡因子，不平衡的节点又如何调整为平衡的呢？和插入节点一样。

插入节点是插入一个节点后从叶子节点计算高度，然后再到父节点根据左右子树的高度计算平衡因子，接着更新高度，再到上一个父节点，直到整个二叉树的顶点。

删除节点可以看作是包含插入节点的，因为删除一个节点后会从左右子树中拉上来一个节点，不会再从叶子节点从新计算高度了，而是从左右子树开始接着更新高度和计算平衡因子。

动画

算法动画视频地址

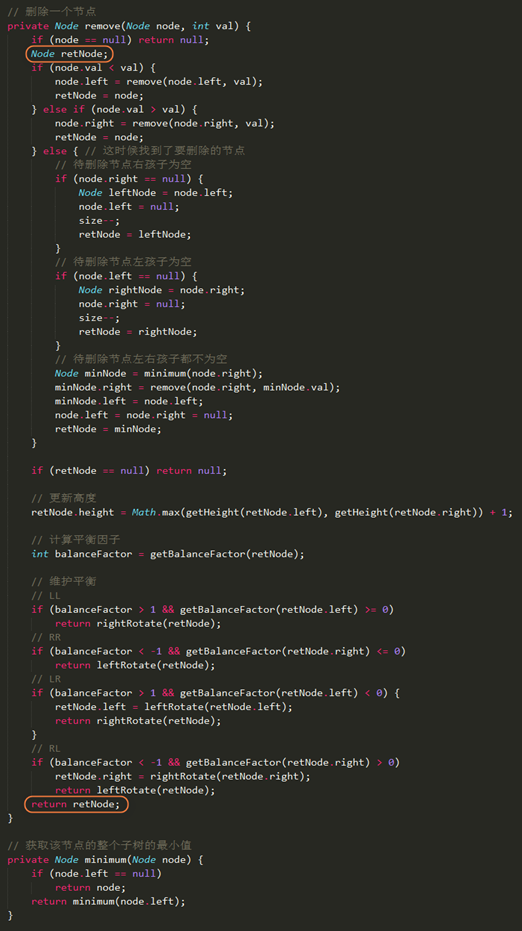
Code

长按下图二维码关注公众号，「算法无遗策」持续更新算法