@loj - 3022@ 「CQOI2017」老 C 的方块

目录

• @description@
• @solution@
• @accepted code@
• @details@

---

@description@

老 C 是个程序员。

作为一个懒惰的程序员，老 C 经常在电脑上玩方块游戏消磨时间。游戏被限定在一个由小方格排成的 R 行 C 列网格上，如果两个小方格有公共的边，就称它们是相邻的，而且有些相邻的小方格之间的公共边比较特殊。

特殊的公共边排列得有很强的规律。首先规定，第 1 行的前两个小方格之间的边是特殊边。然后，特殊边在水平方向上每 4 个小方格为一个周期，在竖直方向上每 2 个小方格为一个周期。所有的奇数列与下一列之间都有特殊边，且所在行的编号从左到右奇偶交替。

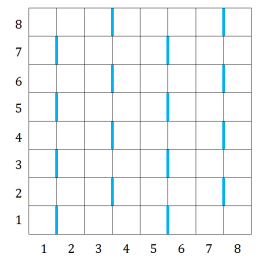
下图所示是一个 R = C = 8 的网格，蓝色标注的边是特殊边。

首先，在第 1 行，第 1 列和第 2 列之间有一条特殊边。因为竖直方向周期为 2，所以所有的奇数行，第 1 列和第 2 列之间都有特殊边。因为水平方向周期为 4，所以所有奇数行的第 5 列和第 6 列之间也有特殊边，如果网格足够大，所有奇数行的第 9 列和第 10 列、第 13 列和第 14 列之间都有特殊边。

因为所有的奇数列和下一列之间都有特殊边，所以第 3 列和第 4 列、第 7 列和第 8 列之间也有特殊边，而所在行的编号从左到右奇偶交替，所以它们的特殊边在偶数行。如果网格的规模更大，我们可以用同样的方法找出所有的特殊边。

网格的每个小方格刚好可以放入一个小方块，在游戏的一开始，有些小方格已经放上了小方块，另外的小方格没有放。

老 C 很讨厌下图所示的图形，如果他发现有一些小方块排列成了它讨厌的形状（特殊边的位置也要如图中所示），就很容易弃疗，即使是经过任意次旋转、翻转后排列成讨厌的形状，老 C 也同样容易弃疗。

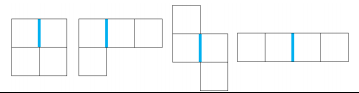
为了防止弃疗，老 C 决定趁自己还没有弃疗，赶紧移除一些格子里小方块，使得剩下的小方块不能构成它讨厌的形状。但是游戏里每移除一个方块都是要花费一些金币的，每个方块需要花费的金币有多有少参差不齐。老 C 当然希望尽可能少的使用游戏里的金币，但是最少要花费多少金币呢？老 C 懒得思考，就把这个问题交给你了。

输入格式

第一行有 3 个正整数 C, R, n，表示 C 列 R 行的网格中，有 n 个小方格放了小方块。

接下来 n 行，每行 3 个正整数 x, y, w，表示在第 x 列第 y 行的小方格里放了小方块，移除它需要花费 w 个金币。保证不会重复，且都在网格范围内。

输出格式

输出一行，包含一个整数，表示最少花费的金币数量。

样例

样例输入 1

2 2 4

1 1 5

1 2 6

2 1 7

2 2 8

样例输入 1

5

样例输入 2

3 3 7

1 1 10

1 2 15

1 3 10

2 1 10

2 2 10

2 3 10

3 1 10

样例输出 2

15

数据范围与提示

1 <= C, R, n <= 10^5, 1 <= w <= 10^4。

@solution@

题意绕晕人.jpg。

但实际上有用的信息全在图片里面 2333。

假如第 x 列第 y 行的 (x, y) 与 (x + 1, y) 同时存在，且它们之间有特殊边（即图片上的蓝色边），则必须要从如下的几种选择中选择一种：

（1）删除 (x, y) 或 (x + 1, y)（这个地方显然是选择删除费用较小的那个）。

（2）删除 (x, y) 周围除了 (x + 1, y) 以外相邻的 3 个 (x - 1, y), (x, y - 1), (x, y + 1)（如果它们存在）。

（3）删除 (x + 1, y) 周围除了 (x, y) 以外相邻的 3 个 (x + 2, y), (x + 1, y - 1), (x + 1, y + 1)（如果它们存在）。

“必须从几种选择中选择一种” 并且求最小花费，联想到最小割。

考虑将那些与特殊边不相邻的点拿出来，进行黑白染色（这里的染色不是平常的相邻染成异色，而是上面所说的 (x, y) 周围的三个点染成同色，(x + 1, y) 周围三个点染成同色，且 (x, y) 与 (x + 1, y) 周围的点为异色）。

将源点连黑点，容量为题目中所说的 w；将白点连汇点，容量为题目中所说的 w。

假如第 x 列第 y 行的 (x, y) 与 (x + 1, y) 同时存在，则 (x, y) 和 (x + 1, y) 之间连边，容量为 min(w1, w2)（分别表示两个格子删除的费用），方向看它们周围的格子颜色是什么：如果 (x, y) 与黑色相邻则 (x, y) -> (x + 1, y)；否则 (x + 1, y) -> (x, y)。

然后周围的黑点向它相邻的点连，它们向周围的白点连边，容量都为 inf。

可以发现这样连出来是可以满足我们所需要的限制。

不要问我为什么 10^5 跑得过，问就是形而上学。

@accepted code@

#include<map>
#include<cstdio>
#include<iostream>
using namespace std;
typedef pair<int, int> pii;
const int MAXN = 100000;
const int MAXV = 2*MAXN;
const int MAXE = 20*MAXV;
const int INF = int(1E9);
const pii d1[] = {make_pair(0, 1), make_pair(0, -1), make_pair(1, 0)};
const pii d2[] = {make_pair(0, 1), make_pair(0, -1), make_pair(-1, 0)};
struct Graph{
	struct edge{
		edge *nxt, *rev;
		int to, cap, flow;
	}edges[MAXE + 5], *adj[MAXV + 5], *ecnt;
	int s, t, d[MAXV + 5], vd[MAXV + 5];
	void init() {ecnt = &edges[0];}
	void addedge(int u, int v, int c) {
		edge *p = (++ecnt), *q = (++ecnt);
		p->to = v, p->cap = c, p->flow = 0;
		p->nxt = adj[u], adj[u] = p;
		q->to = u, q->cap = 0, q->flow = 0;
		q->nxt = adj[v], adj[v] = q;
		p->rev = q, q->rev = p;
//		printf("! %d %d %d\n", u, v, c);
	}
	int aug(int x, int tot) {
		if( x == t ) return tot;
		int sum = 0, mind = t + 1;
		for(edge *p=adj[x];p;p=p->nxt) {
			if( p->cap != p->flow ) {
				if( d[p->to] + 1 == d[x] ) {
					int del = aug(p->to, min(tot - sum, p->cap - p->flow));
					p->flow += del, p->rev->flow -= del, sum += del;
					if( sum == tot || d[s] == t + 1 ) return sum;
				}
				mind = min(mind, d[p->to]);
			}
		}
		if( sum == 0 ) {
			vd[d[x]]--;
			if( vd[d[x]] == 0 ) {
				d[s] = t + 1;
				return sum;
			}
			d[x] = mind + 1;
			vd[d[x]]++;
		}
		return sum;
	}
	int max_flow(int _s, int _t) {
		s = _s, t = _t;
		int flow = 0;
		while( d[s] != t + 1 )
			flow += aug(s, INF);
		return flow;
	}
}G;
map<pii, int>mp;
int C, R, n;
pii p[MAXN + 5]; int w[MAXN + 5];
int func(pii p) {
	if( p.second & 1 ) return (p.first - 1) % 4;
	else return (p.first - 1) % 4 + 4;
}
int main() {
	scanf("%d%d%d", &C, &R, &n), G.init();
	for(int i=1;i<=n;i++)
		scanf("%d%d%d", &p[i].first, &p[i].second, &w[i]), mp[p[i]] = i;
	int s = n + 1, t = n + 2;
	for(int i=1;i<=n;i++) {
		int type = func(p[i]);
		if( type == 4 || type == 3 )
			G.addedge(s, i, w[i]);
		if( type == 5 || type == 2 )
			G.addedge(i, t, w[i]);
		if( type == 0 ) {
			if( mp.count(make_pair(p[i].first + 1, p[i].second)) ) {
				int j = mp[make_pair(p[i].first + 1, p[i].second)];
				G.addedge(i, j, min(w[i], w[j]));
				for(int k=0;k<3;k++)
					if( mp.count(make_pair(p[j].first + d1[k].first, p[j].second + d1[k].second)) )
						G.addedge(j, mp[make_pair(p[j].first + d1[k].first, p[j].second + d1[k].second)], INF);
				for(int k=0;k<3;k++)
					if( mp.count(make_pair(p[i].first + d2[k].first, p[i].second + d2[k].second)) )
						G.addedge(mp[make_pair(p[i].first + d2[k].first, p[i].second + d2[k].second)], i, INF);
			}
		}
		if( type == 6 ) {
			if( mp.count(make_pair(p[i].first + 1, p[i].second)) ) {
				int j = mp[make_pair(p[i].first + 1, p[i].second)];
				G.addedge(j, i, min(w[i], w[j]));
				for(int k=0;k<3;k++)
					if( mp.count(make_pair(p[j].first + d1[k].first, p[j].second + d1[k].second)) )
						G.addedge(mp[make_pair(p[j].first + d1[k].first, p[j].second + d1[k].second)], j, INF);
				for(int k=0;k<3;k++)
					if( mp.count(make_pair(p[i].first + d2[k].first, p[i].second + d2[k].second)) )
						G.addedge(i, mp[make_pair(p[i].first + d2[k].first, p[i].second + d2[k].second)], INF);
			}
		}
	}
	printf("%d\n", G.max_flow(s, t));
}

@details@

注意！它题目中说的是！第 x 列第 y 行！！！

被这个题意卡到自闭。以为自己读懂了结果样例一看好像不大对。。。