IntelliJ IDEA community 安装教程

jetbrains官网下载 IntelliJ IDEA安装包

https://www.jetbrains.com/idea/download/#section=windows

此处选择社区版的zip文件

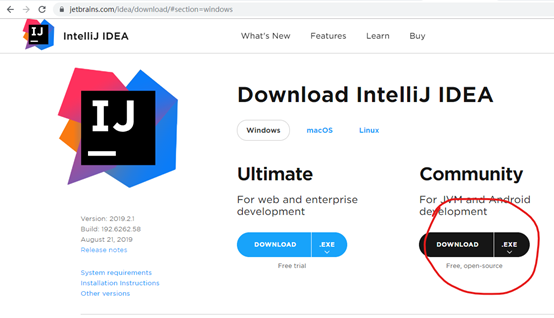
下载完成后解压安装包，
此处解压目录为 E:\IntelliJ IDEA\

开始安装
首先添加环境变量
鼠标右键我的电脑->属性，点击高级系统设置，设置环境变量

找到path环境变量添加刚才解压文件bin目录，注意两边的“;”
此处为我的解压目录   E:\ IntelliJ IDEA\bin;

在用户目录(一般为C:\user\用户名)下创建.IdeaIC2019.2/config目录，然后创建文件idea64.exe.vmoptions
(具体内容参考刚才解压文件下的/bin/idea64.exe.vmoptions文件)，这个文件主要是控制JVM虚拟机的参数，日志，策略等。其中最主要的是设置最大堆内存和最小堆内存大小（官方只给了设置-Xms和-Xmx的建议）。

以下是一些JVM的参数设置。
#最小堆内存
-Xms1g

#最大堆内存
-Xmx1g
#最小堆和最大堆内存一致是为了避免每次垃圾回收完成后JVM重新分配内存，官方推荐为物理内存的1/4

#年轻代大小 推荐3/8堆内内存
-Xmn192m

#最小非堆内存
-XX:PermSize=256m

#最大非堆内存,和堆内存一样避免频繁的大小调整
-XX:MaxPermSize=256m

#InteiJ IDEA缓存
-XX:ReservedCodeCacheSize=240m

#CMS垃圾收集器
-XX:+UseConcMarkSweepGC
#并发执行占用CPU资源较多，会在程序初始化时给出警告Option UseConcMarkSweepGC was deprecated in version 9.0 and will likely be rmove in of future relase 可能会在以后版本中移除，现在还可以用。

-XX:SoftRefLRUPolicyMSPerMB=50
#用户指定的忍耐度（VM能够忍耐软引用对象多久没有被回收）如果觉得GC太过频繁的可以设置将此的大一点,官方模板文件设置是50ms

-XX:CICompilerCount=1
#IntelliJ IDEA要求是2以上，设置1会发生失败

-XX:+HeapDumpOnOutOfMemoryError
#当JVM发生OOM时，自动生成DUMP文件，可以追踪堆栈信息

我的电脑有8G内存,以下是我的配置文件内容：

-Xms1g
-Xmx1g
-Xmn192m
-XX:PermSize=256m
-XX:MaxPermSize=256m
-XX:ReservedCodeCacheSize=256m
-XX:+UseConcMarkSweepGC

-ea
-XX:CICompilerCount=2
-Dsun.io.useCanonPrefixCache=false
-Djava.net.preferIPv4Stack=true
-Djdk.http.auth.tunneling.disabledSchemes=""
-XX:+HeapDumpOnOutOfMemoryError
-XX:-OmitStackTraceInFastThrow
-Djdk.attach.allowAttachSelf
-Dkotlinx.coroutines.debug=off

　　

在保存完成后打开cmd 命令提示符，cd到解压目录/bin下
输入idea.bat完成程序初始化

到这里，安装工作就基本完成了。
进入主题和插件的选择界面，可以一直点击 next：Default plugins 以后再修改和安装各种主题和插件，也可以一次设置好。

选择主题，可以是Darcula或Light。

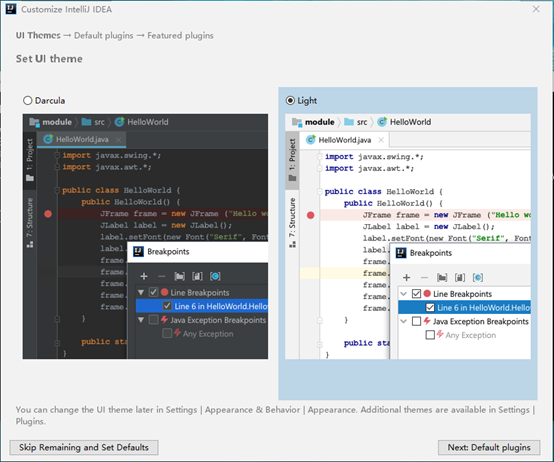
设置插件和你需要的工具

设置完成，出现如下界面

选择Create New Project新建项目

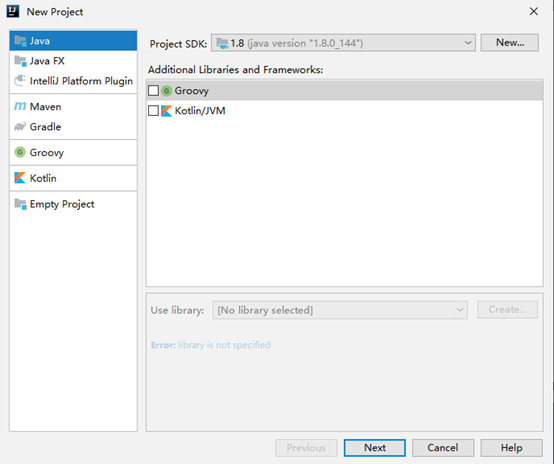
直接next,输入项目名，然后选择从模板创建

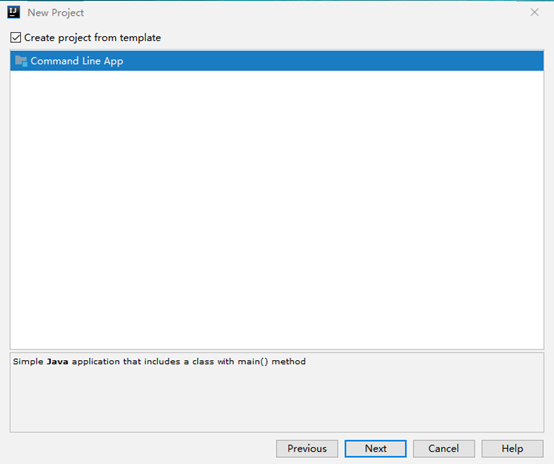
测试一下

完成!

ps:排版一直崩，原地爆炸/(ㄒoㄒ)/~~