UVA 1025 "A Spy in the Metro " （DAG上的动态规划？？ or 背包问题？？）

传送门

参考资料：

　　[1]:算法竞赛入门经典：第九章 DAG上的动态规划

题意：

　　Algorithm城市的地铁有 n 个站台，编号为 1~n，共有 M1+M2 辆列车驶过；

　　其中 M1 辆列车从 1 号站台驶向 n 号站台，M2 辆列车从 n 号站台驶向 1 号地铁；

　　（单程线，M1 辆列车到达 n 号站台后不会回返，同理 M2）

　　特工 Maria 要在 T 时刻到达 n 号站台与特务会面，但为了保证安全，在会面前尽量呆在行进的列车中；

　　现给出你这 M1+M2 辆列车的发车时刻；

　　问如何换乘列车使得特工 Maria 能在 T 时刻前到达 n 号站台，并且在换乘期间在站台的停留时间最短；

　　如果可以在规定时间到达 n 站台，输出在站台停留的最短时间，反之，输出 "impossible"；

题解：

　　看完书上的解释后，感觉，不像是DAG上的动态规划，倒有点像背包的味道；

 int n,t;
 int m1,m2;
 int f[maxn];///前m1辆列车的发车时刻
 int e[maxn];///后m2辆列车的发车时刻
 int c[maxn];///c[i]:车站i到车站i+1的时间花费
 /**
     (i,j):i时刻在车站j
     dp[i][j]:从(i,j)->(t,n)所需等待的最少时间
 */
 int dp[maxn][];
 /**
     hasTrain[i][j][0]=true:i时刻在车站j有到j+1的火车
     hasTrain[i][j][1]=true:i时刻在车站j有到j-1的火车
 */
 bool hasTrain[maxn][][];

　　最关键的便是dp[ i ][ j ]的定义；

　　之所以定义成二维的，是因为决策受当前时间和所处车站的影响，有两个影响因素；

　　定义好后，便是找状态转移方程了；

　　首先预处理出 hasTrain 数组：

 void Init()///预处理hasTrain
 {
     mem(hasTrain,false);
     for(int i=;i <= m1;++i)
     {
         int cnt=f[i];
         hasTrain[cnt][][]=true;
         for(int j=;j <= n;++j)
         {
             cnt += c[j-];
             hasTrain[cnt][j][]=true;
         }
     }
     for(int i=;i <= m2;++i)
     {
         int cnt=e[i];
         hasTrain[cnt][n][]=true;
         for(int j=n-;j >= ;--j)
         {
             cnt += c[j];
             hasTrain[cnt][j][]=true;
         }
     }
 }

预处理hasTrain[]

　　令dp[t][n]=0,dp[t][1,2,...,n-1]=INF;

　　按照时间逆序遍历，对于状态 dp[ i ][ j ]:

　　①等一分钟，下一分钟从车站 j 出发到达(t , n)；

　　②搭乘往右开的列车；

　　③搭乘往左开的列车；

　　

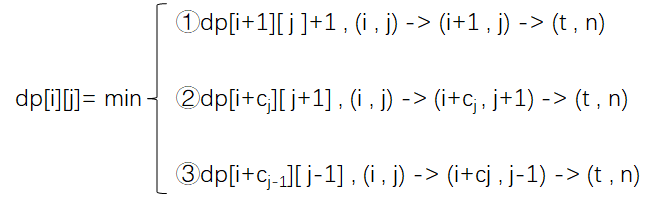
AC代码：

 #include<bits/stdc++.h>
 using namespace std;
 #define INF 0x3f3f3f3f
 #define mem(a,b) memset(a,b,sizeof(a))
 const int maxn=+;
 
 int n,t;
 int m1,m2;
 int f[maxn];///前m1辆列车的发车时刻
 int e[maxn];///后m2辆列车的发车时刻
 int c[maxn];///c[i]:车站i到车站i+1的时间花费
 /**
     (i,j):i时刻在车站j
     dp[i][j]:从(i,j)->(t,n)所需等待的最少时间
 */
 int dp[maxn][];
 /**
     hasTrain[i][j][0]=true:i时刻在车站j有到j+1的火车
     hasTrain[i][j][1]=true:i时刻在车站j有到j-1的火车
 */
 bool hasTrain[maxn][][];
 
 void Init()///预处理hasTrain
 {
     mem(hasTrain,false);
     for(int i=;i <= m1;++i)
     {
         int cnt=f[i];
         hasTrain[cnt][][]=true;
         for(int j=;j <= n;++j)
         {
             cnt += c[j-];
             hasTrain[cnt][j][]=true;
         }
     }
     for(int i=;i <= m2;++i)
     {
         int cnt=e[i];
         hasTrain[cnt][n][]=true;
         for(int j=n-;j >= ;--j)
         {
             cnt += c[j];
             hasTrain[cnt][j][]=true;
         }
     }
 }
 void Solve()
 {
     Init();
     for(int i=;i < n;++i)
         dp[t][i]=INF;
     dp[t][n]=;
     for(int i=t-;i >= ;--i)
     {
         for(int j=;j <= n;++j)
         {
             dp[i][j]=dp[i+][j]+;
             if(j < n && hasTrain[i][j][] && i+c[j] <= t)
                 dp[i][j]=min(dp[i][j],dp[i+c[j]][j+]);
             if(j >  && hasTrain[i][j][] && i+c[j-] <= t)
                 dp[i][j]=min(dp[i][j],dp[i+c[j-]][j-]);
         }
     }
     if(dp[][] >= INF)
         puts("impossible");
     else
         printf("%d\n",dp[][]);
 }
 int main()
 {
     int kase=;
     while(~scanf("%d",&n) && n)
     {
         scanf("%d",&t);
         for(int i=;i < n;++i)
             scanf("%d",c+i);
         scanf("%d",&m1);
         for(int i=;i <= m1;++i)
             scanf("%d",f+i);
         scanf("%d",&m2);
         for(int i=;i <= m2;++i)
             scanf("%d",e+i);
 
         printf("Case Number %d: ",++kase);
         Solve();
     }
     return ;
 }