UVA - 13024 Saint John Festival 凸包+二分

题目链接：https://vjudge.net/problem/UVA-13024

题意：先给出\(L\)个点构造一个凸包，再给出\(S\)个点，询问有几个点在凸包内。

题解：判断点是否在凸包内的模板题。最暴力的想法是\(o(n^2)\)枚举每个点，但实际上我们可以使用二分优化。具体操作就是以凸包最左侧点为起点，对每个点按斜率排序，然后把凸包分割成数个三角形，在这些三角形中二分查找斜率。复杂度便优化为\(o(nlogn)\)如下图。

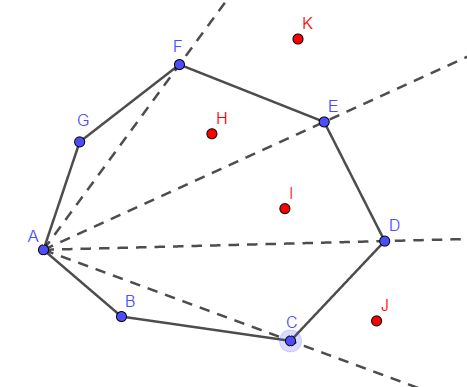
• 在凸包\(ABCDEFG\)中可二分查找\(H\),\(I\),\(J\),\(K\)点

完成二分后，通过叉积判断点是否在凸包内，如下图。

• \(\vec{FH}\times{\vec {HE}} < 0\)，\(\vec{FK}\times{\vec {KE}} > 0\)

即叉积<0则在凸包内，>0在凸包外，同时还有叉积=0的情况（点在凸包的边上）。但是叉积=0时还应考虑一种情况，即在凸包一条边的延长线上，需要特判。如下图。

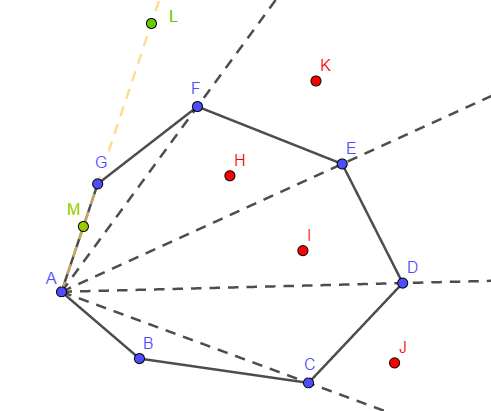
• 如图所示的\(L\)点和\(M\)点叉积均为0。

AC代码：

#include <bits/stdc++.h>
#define SIZE 100007
#define rep(i, a, b) for(int i = a; i <= b; ++i)
using namespace std;
typedef long long ll;
void io() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
}
ll n, m, t, num;
struct Point {
	ll x, y;
	double k;
	friend bool operator<(const Point& a, const Point& b) {    //为使用lower_bound进行运算符重载
		return a.k <= b.k;
	}
};
Point p[SIZE], ch[SIZE], tp[SIZE];
bool cmp(Point a, Point b) {	//andrew算法排序预处理函数
	if (a.x == b.x) return a.y < b.y;
	else return a.x < b.x;
}
ll cross(Point a, Point b, Point c) { return (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x); }
ll crossx(Point a, Point b, Point c) { return (a.x - b.x) * (c.y - a.y) - (a.y - b.y) * (c.x - a.x); }
ll andrew() {	//采用安德鲁算法求凸包，返回顶点数
	sort(p + 1, p + n + 1, cmp);
	ll top = 0;
	for (int i = 1; i <= n; ++i) {
		while ((top > 1) && (cross(ch[top - 1], ch[top], p[i]) <= 0)) --top;
		ch[++top] = p[i];
	}
	ll tmp = top;
	for (int i = n - 1; i; --i) {
		while ((top > tmp) && (cross(ch[top - 1], ch[top], p[i]) <= 0)) --top;
		ch[++top] = p[i];
	}
	if (n > 1) top--;
	return top;
}
bool InConvexHull(ll top, Point x) {	//判断点x是否在凸包内
	ll pos = lower_bound(ch + 1, ch + top + 1, x) - ch - 1;    //二分查找
	if (pos == 1) return false;
	ll j = crossx(x, ch[pos], ch[pos + 1]);
	if (j < 0) return true;
	else if (j == 0) {    //叉积为0时特判
		ll minx = min(ch[pos].x, ch[pos + 1].x), maxx = max(ch[pos].x, ch[pos + 1].x);
		ll miny = min(ch[pos].y, ch[pos + 1].y), maxy = max(ch[pos].y, ch[pos + 1].y);
		if ((minx <= x.x) && (maxx >= x.x) && (miny <= x.y) && (maxy >= x.y)) return true;
		else return false;
	}
	else return false;
}
int main() {
	io();
	while (cin >> n && n) {    //多组输入
		num = 0;
		rep(i, 1, n) cin >> p[i].x >> p[i].y;
		cin >> m;
		ll top = andrew();
		ll x = ch[1].x, y = ch[1].y;
		rep(i, 2, top) {	//计算斜率
			double tx = ch[i].x - x, ty = ch[i].y - y;
			if (!tx) {	//若x坐标相同，则斜率设为1e18
				if (ty < 0) ch[i].k = -1e18;
				else ch[i].k = 1e18;
			}
			else ch[i].k = 1.0 * ty / tx;
		}
		ch[1].k = -1e18;
		rep(i, 1, m) {
			cin >> tp[i].x >> tp[i].y;
			if (ch[1].x > tp[i].x) continue;
			ll tx = tp[i].x - x, ty = tp[i].y - y;
			Point x;
			if (!tx) {
				if (ty < 0) x.k = -1e18;
				else x.k = 1e18;
			}
			else x.k = 1.0 * ty / tx;
			x.x = tp[i].x, x.y = tp[i].y;
			if (InConvexHull(top, x)) ++num;	//计数
		}
		cout << num << endl;
	}
}