loj6402 校门外的树(dp，多项式求逆)

https://loj.ac/problem/6402

庆祝一下，，，第一个我自己做出来的，，，多项式的题（没办法，我太弱

虽然用了2个小时才想出来，但这毕竟是0的突破……

首先声明，虽然我写的题解很长，但是大部分都是证明和废话

第一步，转化题意(用时30min)：

一个1~n的全排列$p$，如果存在$i<j,p[i]<p[j]$，那么就把$i$和$j$之间连一条边。

问所有p的所有排列方案，最后联通块的大小的乘积，的和。

因为原题中$a$是随机的实数，所以说我们可以不用考虑有$a_i=a_j$的情况。

因为最后用到的只有相对的大小关系，所以可以直接转化成一个1~n的排列$p$。

其实很多时间都花在"诶，是这个意思吗，不会啊"，"哦，不对，看错题了"。

第二步，找规律推性质(用时50min)：

我们发现，一个联通块，一定是$l$到$r$连续的一段。

假如说，$a$和$b$在同一个联通块内(令$a<b$)，存在$c$满足$a<c<b$，并且$c$不在$a$和$b$所在联通块内。

我们来证明这种情况是不存在的。

首先，$p[b]<p[c]<p[a]$，否则$c$与$a$、$b$有直接的边相连。

那么$p[a]>p[b]$，但是他们在同一个联通块内，

所以一定存在一个位置$x$满足$x<a,p[x]<p[b]$或者$x>b,p[x]>p[a]$

那么$x$一定与$c$直接相连，所以证出矛盾。

同理，我们可以证到一个联通块的$p$也是连续的一段。

但是我不是这么找到这个性质的，因为我上面的方法只是证明了这个性质，但是如果我猜不到这个性质……

我按照套路思考，每个联通块找一个代表员好了，找谁呢，那就$p$最小的那个吧。

我们把点放在一个平面上，第$i$个点的坐标是$(i,p[i])$。

我们按照$p$从小到大，加入每个点。

首先，$p$最小的那个点加入的时候，我们考虑找它所在的联通块的点。

找到一个满足$p[j]>p[i]$的最大的$j$，那么$i$到$j$这个连续区间的所有点都在同一个联通块内。

(把这些点分成$p[x]<p[j]$，$p[x]>p[j]>p[i]$两种情况讨论就可以了)

然后$<i$的一些点，也可能在这个联通块内。

然后我们把这些点删掉，再找到$p$最小的那个点，递归下去。

我们发现，我们把一个n*n的矩形，一次一次的减去一个联通块所在的"势力范围"，其实是一次一次砍掉了右边的一条和下面的一条，剩下的还是一个矩形。

如图：

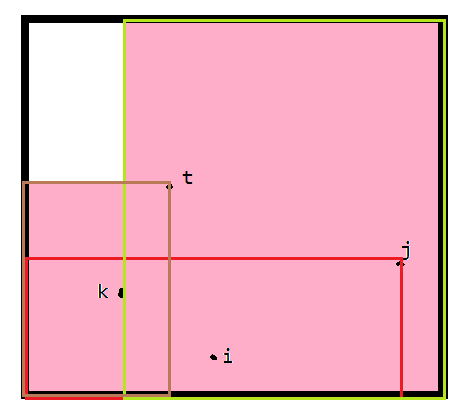
其中淡粉色是一个联通块的势力范围，$t$是这个联通块$p$最大的点，$k$是这个联通块最靠左(就是编号最小)的点。

我们再找下一个联通块的时候，下一个联通块势力范围一定是在白色部分。

所以下一个联通块的$p$最小的点的一定有$p[x]>p[t]$，编号最大的点$x<k$

于是我们两个性质都找到啦。

有了这两个性质之后，我们可以发现，一个联通块$[l,r]$，一定满足：$p[l],p[l+1],....,p[r-1],p[r]$一定是$n-l+1,n-(l+1)+1,....,n-r+1$的一个排列。

同时$p[1],p[2],....,p[r]$一定是$n,n-1,...,n-r+1$的一个排列。

同时$[l,r-1]$中不存在$x$满足$p[1],p[2],....,p[x]$是$n,n-1,....,n-x+1$的一个排列，否则就可以分出$[l,x],[x+1,r]$两个联通块了。

也就是说，如果我们称满足$p[1],p[2],....,p[x]$是$n,n-1,....,n-x+1$的一个排列的$x$是好的，那么每个$x$都一定是一个联通块的右端点。

第三步，推式子(用时40min)：

有了上面的几个性质，我们可以开始列$dp$方程了。

我们令$f(n)$表示1~n的一个排列，除$n$位置外，不存在其他位置是好的，的方案数。

那么$f(0)=0,f(1)=1$

$f(n)=n!-\sum\limits_{i=1}^{n-1} i! f(n-i)$

令$g(n)=n!$，特别地，我们规定$g(0)=1$

那么$f(n)=g(n)-\sum\limits_{i=1}^{n-1} g(i) f(n-i)$

把$\sum$移到左边，可以得到$\sum\limits_{i=0}^{n} g(i) f(n-i) = g(n)$

我们发现这是一个卷积形式$f*g+1=g$。(因为$f(0)=0,g(0)=1$)

令$dp(i)$表示前$i$个数，并且$i$是一个联通块右端点，的贡献。规定$dp(0)=1$

枚举上一个联通块的右端点，那么有：

$dp(n)=\sum\limits_{i=0}^{n} (n-i) f(n-i) dp(i)$

令$h(n)=nf(n)$。$h(0)=0$

$dp(n)=\sum\limits_{i=0}^{n} h(n-i) dp(i)$

又是一个卷积形式$dp=dp*h+1$。(因为$h(0)=0,dp(0)=1$)

于是两次多项式求逆就可以解决问题啦。

//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
const ll mod=998244353,B=3;
const int maxn=1e7+7;
ll n,g[maxn],h[maxn],ginv[maxn],hinv[maxn],X[maxn];

template<typename T>void read(T& aa) {
	aa=0;char cc=getchar();T ff=1;
	while((cc!='-')&&(cc<'0'||cc>'9')) cc=getchar();
	if(cc=='-') ff=-1,cc=getchar();
	while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
	aa*=ff;
}

ll qp(ll x,ll k) {
	ll rs=1;
	while(k) {
		if(k&1) rs=rs*x%mod;
		k>>=1; x=x*x%mod;
	}
	return rs;
}

ll finv(ll x) {return qp(x,mod-2);}

ll qp1(ll x,ll k) {
	if(k<0) return qp(finv(x),-k);
	return qp(x,k);
}

void Rader(ll F[],ll len) {
	for(int i=1,j=len>>1,k;i<len-1;++i) {
		if(i<j) swap(F[i],F[j]);
		k=len>>1;
		while(j>=k) {j-=k;k>>=1;}
		if(j<k) j+=k;
	}
}

void FFT(ll F[],ll len,ll on) {
	Rader(F,len);
	for(int h=2;h<=len;h<<=1) {
		ll wn=qp1(B,(mod-1)*on/h);
		for(int j=0;j<len;j+=h) {
			ll w=1;
			for(int i=j;i<j+h/2;++i) {
				ll u=F[i],v=w*F[i+h/2]%mod;
				F[i]=(u+v)%mod;
				F[i+h/2]=(u-v+mod)%mod;
				w=w*wn%mod;
			}
		}
	}
	ll x=finv(len);
	if(on==-1) For(i,0,len) F[i]=F[i]*x%mod;
}

void get_inv(ll N,ll* A,ll* B) {
	if(N==1) {
		B[0]=finv(A[0]);
		return;
	}
	get_inv((N+1)>>1,A,B);
	ll n=1;for(;n<=(N<<1);n<<=1);
	For(i,0,N-1) X[i]=A[i]; For(i,N,n) X[i]=B[i]=0;
	FFT(X,n,1); FFT(B,n,1);
	For(i,0,n) B[i]=B[i]*(2-B[i]*X[i]%mod+mod)%mod;
	FFT(B,n,-1); For(i,N,n) B[i]=0;
}

int main() {
	read(n);
	g[0]=1; For(i,1,n) g[i]=g[i-1]*(ll)i%mod;
	get_inv(n+1,g,ginv);
	For(i,1,n) h[i]=ginv[i]*(ll)i%mod;
	h[0]=1;
	get_inv(n+1,h,hinv);
	printf("%lld\n",hinv[n]);
	return 0;
}