【Read a good book, that is conversation with many a noble man.】---勒内·笛卡尔（1596-1650）

解答：

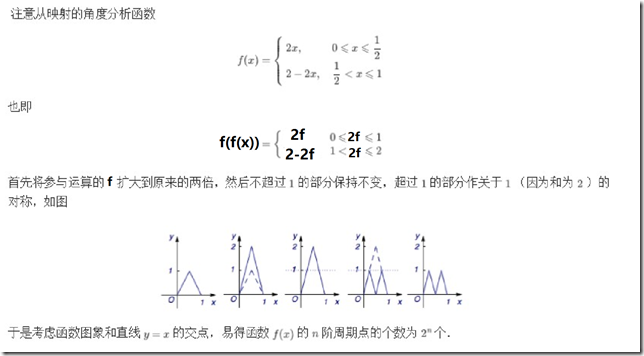
评：也可以把f(f(x))的表达式写出来再作图。相比之下比较花时间.

MT【59】一道迭代函数作图的更多相关文章

  1. javascript学习笔记--迭代函数

    概要 这里的迭代函数指的是对数组对象的操作方法,js数组共有五个迭代函数:every.fifter.forEach.map.some. 1.every every方法,返回值为Boolean类型,tr ...

  2. 混沌分形之迭代函数系统（IFS）

    IFS是分形的重要分支.它是分形图像处理中最富生命力而且最具有广阔应用前景的领域之一.这一工作最早可以追溯到Hutchinson于1981年对自相似集的研究.美国科学家M.F.Barnsley于198 ...

  3. Mathematica 迭代函数

    学习Mathematica迭代函数的几个画图例子: 1.三角形沿着某一点旋转 verticse = {{0, 0}, {1, 0}, {1/2, Sqrt[3]/2}}; tri = Line[ver ...

  4. JavaScript的迭代函数与迭代函数的实现

    前言 ​ 如果对技术很自信,请直接看 实现的源码 ​ 如果想回顾一下基础,请按文章顺序阅读 说到迭代方法,最先想到的是什么?forEach还是map,迭代的方法ES5提供了5种方法 以下定义来自 Ja ...

  5. JavaScript图形实例：迭代函数系统生成图形

    迭代函数系统(Iterated Function System,IFS)可以用来创建分形图案,它是分形理论的重要分支,也是分形图形处理中最富生命力而且最具有广阔应用前景的领域之一.这一工作最早可以追溯 ...

  6. 文件处理，三元操作符，seek()函数，迭代函数和列表解析，reduce函数

    1.文件读取方类型 r,r+,w,x,a, r,读文件 w,写文件,文件内容全部删除,并将新内容从第一行开始赋值 x,写文件,只有文件不存在,可写,文件存在,报错 a,在文件莫问追加信息 r+,w+, ...

  7. MT【294】函数定义的理解

    已知函数$f(x)$的定义域为$D,\pi\in D$.若$f(x)$的图像绕坐标原点逆时针旋转$\dfrac{\pi}{3}$后与原图像重合,则$f(\pi)$不可能是(    )A$\dfrac{ ...

  8. 迭代函数：zip、enumerate，list解析

    #encoding:utf-8 """ 并行迭代: zip enumerate 获取元素及下标 list解析 iter """ #zip # ...

  9. MT【77】函数的定义理解

    答案:D.比如C 中令$x^2+1=2,x=-1,1,$ 得$f(2)=0,2$与定义矛盾,A,B同理排除. D中注意到$x^2-2x$与$|x-1|$对称轴都是$x=1$. 评:函数的定义,首先是两 ...

随机推荐

  1. Luogu4199 万径人踪灭 FFT、Manacher

    传送门 先不考虑”不是连续的一段“这一个约束条件.可以知道:第$i$位与第$j$位相同,可以对第$\frac{i+j}{2}$位置上产生$1$的贡献(如果$i+j$为奇数表明它会对一条缝产生$1$的贡 ...

  2. QT 小总结

    遇到的问题: 1:在debug模式下可以顺利执行,但是换到release模式下没法执行了.会显示 exited with code 1 . 解决办法:把产生的release文件放到QT的bin库下,看 ...

  3. Sql_join left right

    1.内连接inner join 只返回两张表中所有满足连接条件的行,即使用比较运算符根据每个表中共有的列的值匹配两个表中的行.(inner关键字是可省略的) ①传统的连接写法: 在FROM子句中列出所 ...

  4. Ubuntu16.04下安装QQ的完整操作记录（经验证可用）

    本机安装了Ubuntu16.04系统,用于日常运维办公.打算在Ubuntu上安装QQ,如下操作记录也使用于Ubuntu18.04: 1)先下载特制的QQ程序包(其实就是基于Wine容器做了一些封装,程 ...

  5. ProxySQL实现Mysql读写分离 - 部署手册

    ProxySQL是一个高性能的MySQL中间件,拥有强大的规则引擎.ProxySQL是用C++语言开发的,也是percona推的一款中间件,虽然也是一个轻量级产品,但性能很好(据测试,能处理千亿级的数 ...

  6. ruby安装及升级

    在centos6.x下执行上面的"gem install redis"操作可能会报错,坑很多!默认yum安装的ruby版本是1.8.7,版本太低,需要升级到ruby2.2以上,否则 ...

  7. PLSQL使用技巧 如何设置默认显示My Objects、记住密码等

    https://www.cnblogs.com/yilinzi/p/7144852.html PL/SQL Developer实现双击table查询 https://blog.csdn.net/zhy ...

  8. php 多个文件压缩到一起存储

    $zip = new ZipArchive();$res = $zip->open('test.zip', ZipArchive::CREATE); //不存在则创建$filepath = 's ...

  9. JQuery监听页面滚动总结

    1.当前滚动的地方的窗口顶端到整个页面顶端的距离: var winPos = $(window).scrollTop(); 2.获取指定元素的页面位置: $(val).offset().top; 3. ...

  10. 最新一课 老师指点用Listview适配器

    上课前 <?xml version="1.0" encoding="utf-8"?>    <ScrollView xmlns:android ...