20175310 迭代和JDB

迭代和JDB

1 使用C(n,m)=C(n-1,m-1)+C(n-1,m)公式进行递归编程实现求组合数C(m,n)的功能

zuheshu.java文件夹下的代码：

import java.util.Scanner;
public class zuheshu {
    public static void main(String args[]) {
       qiuzhi a=new qiuzhi();
       System.out.println("输入m");
       Scanner reader1=new Scanner(System.in);
       int m=reader1.nextInt();
       System.out.println("输入n");
       Scanner reader2=new Scanner(System.in);
       int n=reader2.nextInt();
       if(m>n)              //异常情况m>n
           return;
       int result=qiuzhi.zuhe(n,m);
       System.out.println("组合数C(n,m)的结果是"+result);
    }
}

qiuzhi.java文件夹下的代码：

class qiuzhi{
       static int zuhe(int n,int m){    //求组合数C(n,m)的值
           if (m==0)
              return 1;
           else if (n==m)
              return 1;
           else
              return zuhe(n-1,m-1)+zuhe(n-1,m);
       }
}

2 m,n 要通过命令行传入

之前没有看清题意，没有理解用命令行输入的意思，上面zuheshu.java的源代码是通过scanner输入的，而非命令行。通过网上查找资料，了解到命令行的输入不是用scanner，修改zuheshu.java后的程序如下：

public class zuheshu {
    public static void main(String args[]) {
       qiuzhi a=new qiuzhi();
       int []num = new int[args.length];
       for (int i=0;i<args.length;i++){
            num[i]=Integer.valueOf(args[i]);
        }
       int n=num[0];
       int m=num[1];
       if(m>n){
           System.out.println("输入格式错误！");     //异常情况m>n
           return;
       }
       int result=qiuzhi.zuhe(n,m);
       System.out.println("组合数C(n,m)的结果是"+result);
    }
}

3 测试运行截图

正常情况c(3,2)

异常情况c(2, 3)

边界情况c(3,3)

4 正常情况下用JDB调试程序c(3,2)

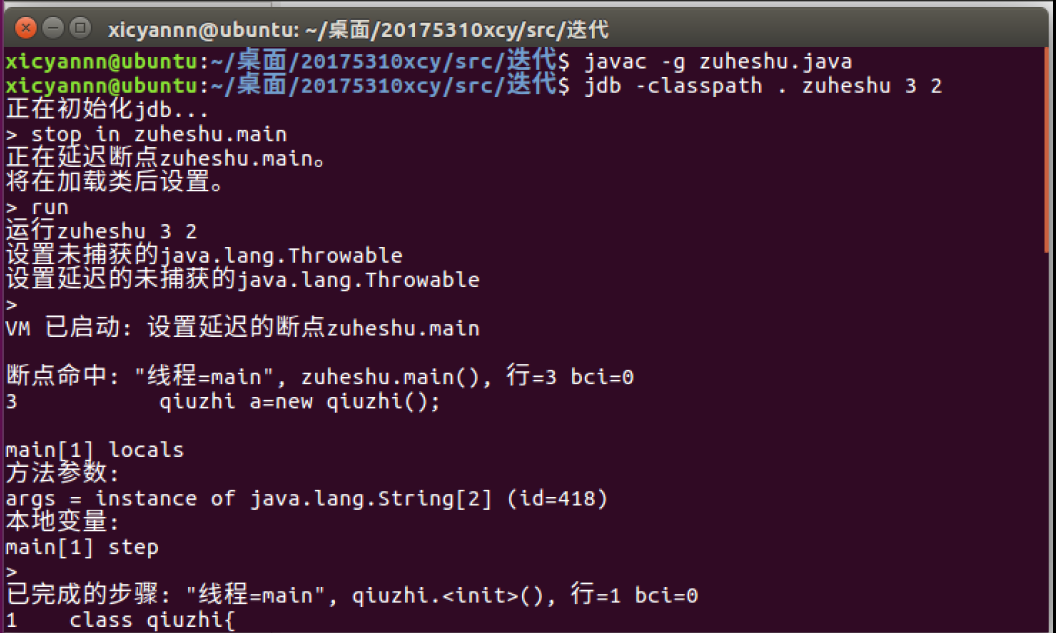
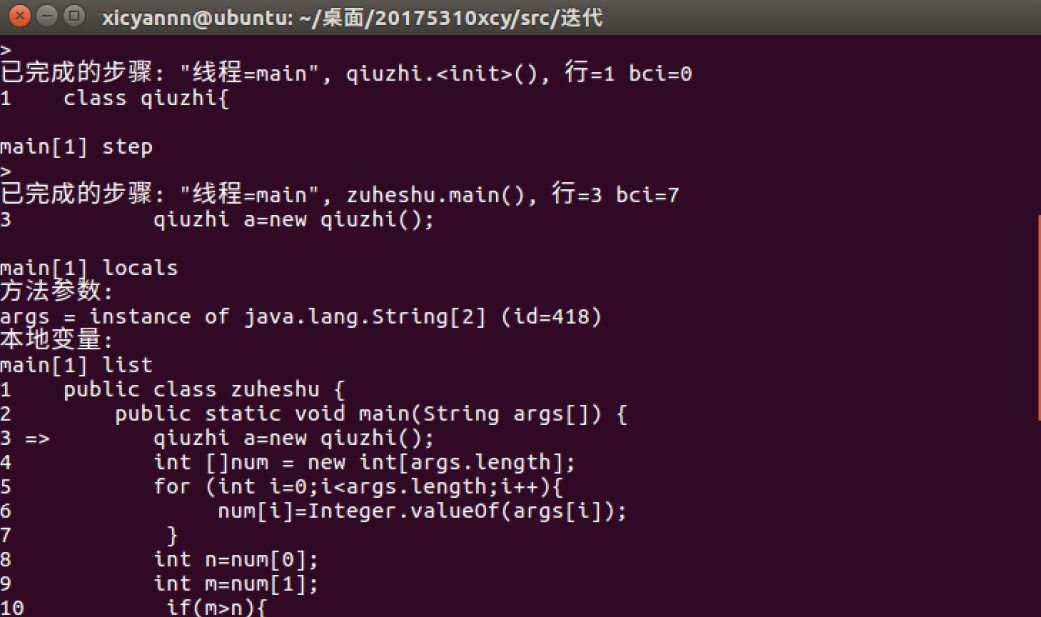
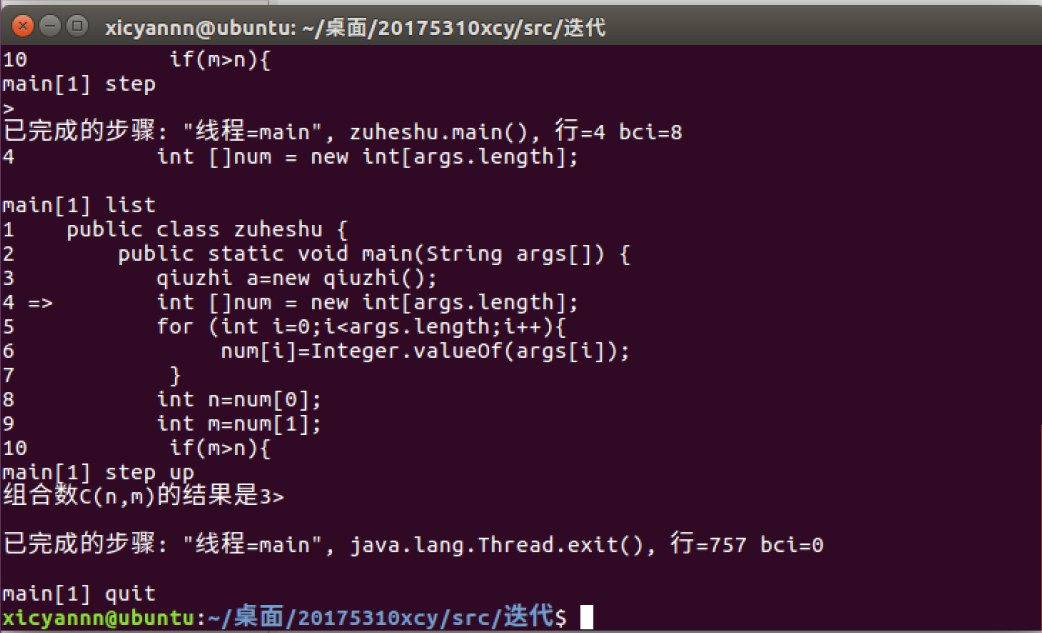
问题及解决：

• 问题1：
  
  在做选做作业迭代时，编译源文件报错如下图
  
  

• 问题1解决方案：
  
  第一个错误我想表达的意思是当输入错误的时候退出程序，结果我用的是C语言的写法return 0，应该直接return就可以了。
  
  

• 问题2：
  
  无法从静态上下文中引用非静态方法

• 问题2解决方案：
  
  我发现我的主类zuheshu中含有static，属于静态，而另一个类qiuzhi中不含static，因此不是静态。所以我就在类qiuzhi中加了关键字static，编译运行就对了。
  
  

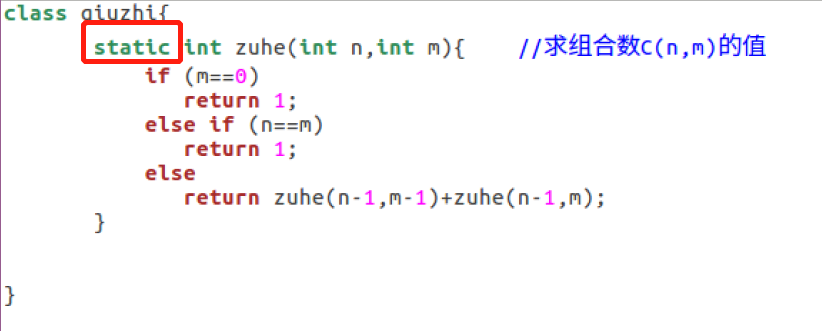
• 问题3：
  
  在用JDB调试时出错
  
  

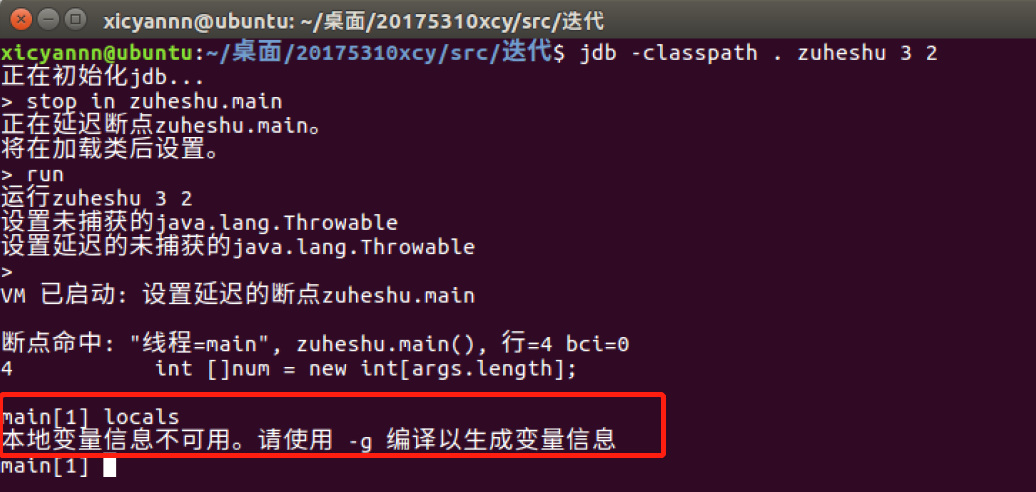
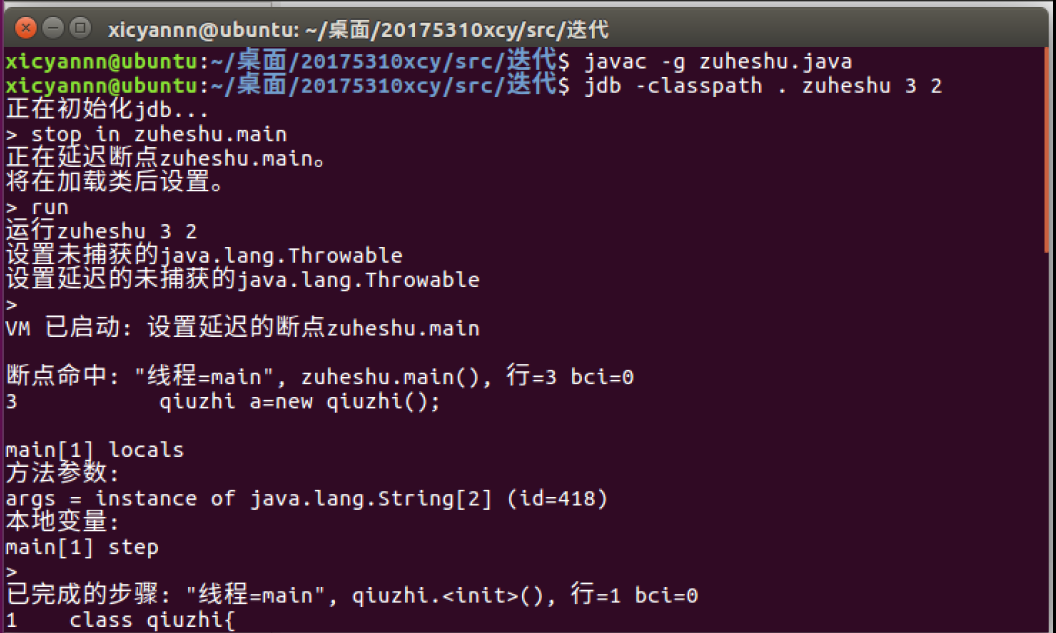
• 问题3解决方案：
  
  参考了娄老师的博客(http://www.cnblogs.com/rocedu/p/6371262.html)，使用javac -g -d bin src/HelloJDB.java对程序进行编译。注意javac中-g参数是为了产生各种调试信息，一定要加上，否则无法调试。