[CF1041F Ray in the tube][数学]
http://codeforces.com/contest/1041/problem/F
题目大意:
下边界有n个给定点,上边界有m个给定点,可以从任意一个点发出一条激光,激光碰到边界会反射
激光到达边界必须打到整数点,问最多可以打到几个给定点
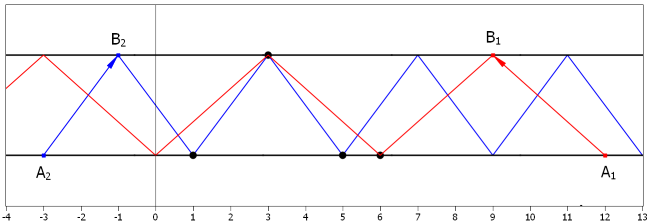
输入格式:
第一行两个整数n,y1,表示下边界给定点的个数和下边界的纵坐标
第二行n个整数,表示给定点的横坐标
第三行两个整数m,y2,表示上边界给定点的个数和上边界的纵坐标
第四行m个整数,表示给定点的横坐标
题解:设起点横坐标为Xa,步长为Dx,则经过的第一行的点满足X=Xa+2*k*Dx,第二行的点满足X=Xa+(2*k+1)*Dx,发现步长为1时经过的点总可以覆盖步长Dx为奇数的点,所以可以通过步长为1来代替步长为奇数的情况,而当步长Dx为偶数时(即Dx=a*b,a为奇数,b为偶数),总可以转化成步长为b的情况,所以偶数都可以转化成步长为2的整数幂的情况,综上可得,只需要枚举2的0~29次幂即可,使用map存下来所有数%(2*Dx)的数量即可
[CF1041F Ray in the tube][数学]的更多相关文章
- CF1041F Ray in the tube
挂上Chester大神的解题报告 有一个思维跳跃的地方,就是不应该枚举所有的$B$点,而是应该在选定一个$A$点之后枚举距离计算. 然后我们发现枚举距离是$2^k$的长度就可以了,证明如下: 假如距离 ...
- CF1041F Ray in the tube构造_思维
不难发现起点必定是一个点. 每次间隔的距离一定是 2k2^k2k,关键就是要判断两点是否在同一跳跃距离上可被同时覆盖. 我们可以对上边进行 x1≡x_{1}\equivx1≡ x2mod(2∗dx) ...
- L - Ray in the tube Gym - 101911L (暴力)
---恢复内容开始--- You are given a tube which is reflective inside represented as two non-coinciding, but ...
- Codeforces 1041F Ray in the tube (看题解)
Ray in the tube 感觉是套路题.. 如果确定一个差值x我们如何取确定答案呢, 我们把a[ i ] -> a[ i ] % (2 * x), 把b[ i ] -> (b[ i ...
- CF 1041 F. Ray in the tube
F. Ray in the tube 链接 题意: 有两条平行于x轴的直线A,B,每条直线上的某些位置有传感器.你需要确定A,B轴上任意两个整点位置$x_a$,$x_b$,使得一条光线沿$x_a→x_ ...
- Codeforces | CF1041F 【Ray in the tube】
昨天晚上全机房集体开\(Div2\),因为人傻挂两次\(B\)题的我开场就\(rank2000+\dots qwq\)于是慌乱之中的我就开始胡乱看题(口胡),于是看了\(F\dots\)(全机房似乎也 ...
- Codeforces.1041F.Ray in the tube(思路)
题目链接 \(Description\) 有两条平行于\(x\)轴的直线\(A,B\),每条直线上的某些位置有传感器.你需要确定\(A,B\)轴上任意两个整点位置\(x_A,x_B\),使得一条光线沿 ...
- Codeforces Round #509 (Div. 2) F. Ray in the tube(思维)
题目链接:http://codeforces.com/contest/1041/problem/F 题意:给出一根无限长的管子,在二维坐标上表示为y1 <= y <= y2,其中 y1 上 ...
- 【杂题】cf1041fF. Ray in the tube
死于没有处理边界 题目描述 题目大意 在两面镜子上各选定一个整数位置的点 A 与 B,并从其中一个点向另一个射出一条光线,使得接收到光线的传感器数量尽可能的多.传感器不重叠. 题目分析 我们来初步考虑 ...
随机推荐
- jenkins安装部署全过程
基本配置: 1.Linux安装配置jdk环境 1.1.上传到 Linux 服务器:例如: 上传至: cd /usr/local 1.2.解压: rpm -ivh jdk-8u111-linux-x64 ...
- BZOJ5487: [Usaco2018 Dec]Cowpatibility
Description 研究证明,有一个因素在两头奶牛能否作为朋友和谐共处这方面比其他任何因素都来得重要--她们是不是喜欢同 一种口味的冰激凌!Farmer John的N头奶牛(2≤N≤50,000) ...
- Learning-Python【13】:迭代器和生成器
一.什么是迭代器 迭代指的是一个重复的过程,每一次重复都是基于上一次的结果而来的 # 这里的循环也是一个迭代,每次基于上一次的结果而取值 li = 'hello' i = 0 while i < ...
- LINQ之路12:LINQ Operators之数据转换(Projecting)
本篇继续LINQ Operators的学习,这里我们讨论的是数据转换的两种方式:Select和SelectMany,看似简单常用的两种运算符,却也大有讲究.我们会在本篇详细介绍他们的使用方式和适用的场 ...
- vue--一些预设属性
Babel=> 转换工具,将ES6转换成ES5的转换工具.有些浏览器不支持ES6语法: router=> 路由管理器: vueX=> 一个仓库,存储状态信息: CSS pre-pro ...
- _quest_random
-- 随机任务-- 可以实现玩家随机获取任务-- 小技巧:需要控制物品法防,在_function_menu表配置物品indexID为28 `comment`备注 `questId`任务ID `chan ...
- 线程(六)之LOCK和synchronized
在java.util.concurrent.locks包中有很多Lock的实现类,常用的有ReentrantLock.ReadWriteLock(实现类ReentrantReadWriteLock), ...
- java jdk动态代理学习记录
转载自: https://www.jianshu.com/p/3616c70cb37b JDK自带的动态代理主要是指,实现了InvocationHandler接口的类,会继承一个invoke方法,通过 ...
- OPENAPI规范Swagger
OPENAPI规范 是一种规范,Swagger是一种工具,Swagger帮我们使用OPENAPI更具体更完善,更好. 博客1:https://app.swaggerhub.com/help/index ...
- node.js调用google翻译api
源码下载:https://pan.baidu.com/s/1nxoodst 使用:(只支持get) http://39.106.33.56:3001/translate?text=Failure is ...
