PRML读书笔记_绪论
一、基本名词
泛化(generalization)
训练集所训练的模型对新数据的适用程度。
监督学习(supervised learning)
训练数据的样本包含输入向量以及对应的目标向量。
- 分类( classification ):给每个输入向量分配到有限数量离散标签中的一个。
- 回归( regression ):输出由一个或者多个连续变量组成。
无监督学习(unsupervised learning)
训练数据由一组输入向量 x 组成,没有任何对应的目标值。
- 聚类(clustering):发现数据中相似样本的分组。
- 密度估计(density estimation):决定输入空间中数据的分布。
反馈学习(reinforcement learning)
在给定的条件下,找到合适的动作,使得奖励达到最大值。学习问题没有给定最优输出的用例。这些用例必须在一系列的实验和错误中被发现。
反馈学习的一个通用的特征是探索( exploration )和利用( exploitation )的折中,过分地集中于探索或者利用都会产生较差的结果。
- 探索:是指系统尝试新类型的动作,
- 利用:是指系统使用已知能产生较高奖励的动作。
二、概率论
1.概率论的两个基本规则:加和规则( sumrule )、乘积规则( product rule )
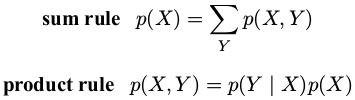
2.贝叶斯定理( Bayes' theorem )
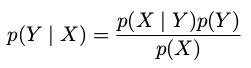
贝叶斯定理中的分母可以用出现在分子中的项表示:
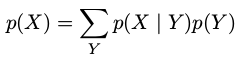
- 先验概率( prior probability ):\(p(Y)\) 在未知\(X\)分布时,我们已知\(Y\)分布,顾称\(p(Y)\)为先验。
- 后验概率( posterior probability ):\(p(Y|X)\) 在得知\(X\)分布后,加入\(p(X)\)的约束可以的到条件概率\(p(Y|X)\),称之为后验。
3.概率密度
概率密度( probability density )
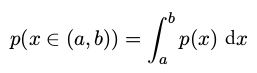
满足下面两个条件:

一个变量的变化\(x = g(y)\) , 那么函数\(f (x)\)就变成了$ f ̃ (y) = f (g(y))$
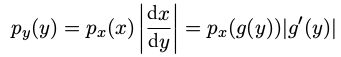
累积分布函数( cumulative distribution function )
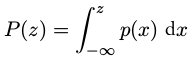
概率密度函数加和规则和乘积规则
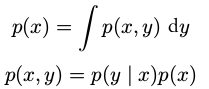
4.期望和协方差
期望( expectation )
离散变量
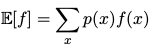
连续变量
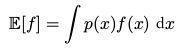
方差( variance )
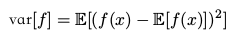
可以化为:
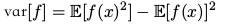
协方差( covariance )
协方差是对两个随机变量 x 和 y而言:

在两个随机向量 x 和 y 的情形下,协方差是一个矩阵:
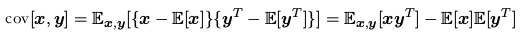
PRML读书笔记_绪论的更多相关文章
- PRML读书笔记_绪论曲线拟合部分
一.最小化误差函数拟合 正则化( regularization )技术涉及到给误差函数增加一个惩罚项,使得系数不会达到很大的值.这种惩罚项最简单的形式采用所有系数的平方和的形式.这推导出了误差函数的修 ...
- PRML读书笔记——3 Linear Models for Regression
Linear Basis Function Models 线性模型的一个关键属性是它是参数的一个线性函数,形式如下: w是参数,x可以是原始的数据,也可以是关于原始数据的一个函数值,这个函数就叫bas ...
- PRML读书笔记——机器学习导论
什么是模式识别(Pattern Recognition)? 按照Bishop的定义,模式识别就是用机器学习的算法从数据中挖掘出有用的pattern. 人们很早就开始学习如何从大量的数据中发现隐藏在背后 ...
- 『TensorFlow』读书笔记_进阶卷积神经网络_分类cifar10_上
完整项目见:Github 完整项目中最终使用了ResNet进行分类,而卷积版本较本篇中结构为了提升训练效果也略有改动 本节主要介绍进阶的卷积神经网络设计相关,数据读入以及增强在下一节再与介绍 网络相关 ...
- 『TensorFlow』读书笔记_进阶卷积神经网络_分类cifar10_下
数据读取部分实现 文中采用了tensorflow的从文件直接读取数据的方式,逻辑流程如下, 实现如下, # Author : Hellcat # Time : 2017/12/9 import os ...
- PRML读书笔记——线性回归模型(上)
本章开始学习第一个有监督学习模型--线性回归模型."线性"在这里的含义仅限定了模型必须是参数的线性函数.而正如我们接下来要看到的,线性回归模型可以是输入变量\(x\)的非线性函数. ...
- The Way to Go读书笔记_第4章_基本结构和基本数据类型
“_”标识符 _ 本身就是一个特殊的标识符,被称为空白标识符.它可以像其他标识符那样用于变量的声明或赋值(任何类型都可以赋值给它),但任何赋给这个标识符的值都将被抛弃,因此这些值不能在后续的代码中使用 ...
- PRML读书笔记——2 Probability Distributions
2.1. Binary Variables 1. Bernoulli distribution, p(x = 1|µ) = µ 2.Binomial distribution + 3.beta dis ...
- PRML读书笔记——Introduction
1.1. Example: Polynomial Curve Fitting 1. Movitate a number of concepts: (1) linear models: Function ...
随机推荐
- PCB (3)创建新工程PCB
点击完成 拖进我们创建的工程中
- leetcode 958. Check Completeness of a Binary Tree 判断是否是完全二叉树 、222. Count Complete Tree Nodes
完全二叉树的定义:若设二叉树的深度为h,除第 h 层外,其它各层 (1-h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树. 解题思路:将树按照层进行遍历,如果 ...
- JavaScript高级程序设计学习(六)之设计模式
每种编程语言都有其自己的设计模式.不禁让人疑惑设计模式是用来做什么?有什么用? 简单的说,设计模式是为了让代码更简洁,更优雅,更完美. 同时设计模式也会让软件的性能更好,同时也会让程序员们更轻松.设计 ...
- PAT A1136 A Delayed Palindrome (20 分)——回文,大整数
Consider a positive integer N written in standard notation with k+1 digits ai as ak⋯a1a0 ...
- POJ2253(dijkstra堆优化)
https://vjudge.net/problem/POJ-2253 Freddy Frog is sitting on a stone in the middle of a lake. Sudde ...
- ESP NVS
简介:NVS的主要功能是:存储键值(存在flash上面): NVS利用spi_flash_{read|write|erase}这些API来操作数据在内存上的删改写,内存上data类型nvs子类型所代表 ...
- 【SPOJ GSS】数据结构题选做
SPOJ GSS1 题意:给一个序列以及一些询问,每个是问\([l,r]\)中最大连续子序列和是多少. 思路:这个问题是以下问题的基础. 我们考虑用线段树来解决这个问题. 首先我们来想想如果要求出最大 ...
- python多版本共存问题(以2.7和3.5系列版本为例)
1.0 下载Python2.7x和Python3.5x版本 2.0 安装Python 3.0 配置环境变量,分别添加至path路径 4.0 只修改Python27文件中的.exe文件(这样系统默认为P ...
- 省市区三级联动,JS实现
文件下载地址:http://files.cnblogs.com/files/chenwolong/jsAddress.rar 示例截图: 在这里自己记录一个方法: function cmbAddOpt ...
- UWP简单示例(三):快速开发2D游戏引擎
准备 IDE:Visual Studio 图形 API:Win2D MSDN 教程:UWP游戏开发 游戏开发涉及哪些技术? 游戏开发是一门复杂的艺术,编码方面你需要考虑图形.输入和网络 以及相对独立的 ...
