DFS实现模板

以如下图的无向图G4为例，进行图的深度优先搜索：

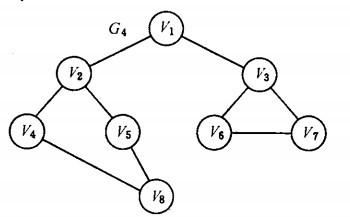
假设从顶点v₁出发进行搜索，在访问了顶点v₁之后，选择邻接点v₂。因为v₂未曾访问，则从v₂出发进行搜索。依次类推，接着从v₄ 、v₈ 、v₅出发进行搜索。在访问了v₅之后，由于v₅的邻接点都已被访问，则搜索回到v₈。由于同样的理由，搜索继续回到v₄，v₂直至v₁，此时由于v₁的另一个邻接点未被访问，则搜索又从v₁到v₃，再继续进行下去由此，得到的顶点访问序列为：

代码：

 /*    图的DFS遍历    */
 //邻接矩阵形式实现
 //顶点从1开始
 #include<iostream>
 #include<cstdio>
 using namespace std;
 const int maxn = ;        //最大顶点数
 typedef int VertexType;     //顶点类型
 bool vis[maxn];  

 struct Graph{               //邻接矩阵表示的图结构
     VertexType vex[maxn];   //存储顶点
     int arc[maxn][maxn];    //邻接矩阵
     int vexnum,arcnum;      //图的当前顶点数和弧数
 };

 void createGraph(Graph &g)  //构建无向图
 {
     cout<<"请输入顶点数和边数：";
     cin>>g.vexnum>>g.arcnum;

     //构造顶点向量
     cout<<"请依次输入各顶点：\n";
     for(int i=;i<=g.vexnum;i++){
         scanf("%d",&g.vex[i]);
     }

     //初始化邻接矩阵
     for(int i=;i<=g.vexnum;i++){
         for(int j=;j<=g.vexnum;j++){
             g.arc[i][j] = ;
         }
     }

     //构造邻接矩阵
     VertexType u,v;     //分别是一条弧的弧尾(起点)和弧头(终点)
     printf("每一行输入一条弧依附的顶点（空格分开）：\n");
     for(int i=;i<=g.arcnum;i++){
         cin>>u>>v;
         g.arc[u][v] = g.arc[v][u] = ;
     }
 }

 //邻接矩阵的深度优先递归算法
 void DFS(Graph g,int i)
 {
     vis[i] = true;
     printf("%d\t",g.vex[i]);                //打印顶点
     for(int j=;j<=g.vexnum;j++){            //遍历每个顶点
         if(g.arc[i][j]== && !vis[j]){        //如果顶点j是顶点i的未访问的邻接点
             DFS(g,j);                        //深度优先搜索顶点j
         }
     }
 }

 //邻接矩阵的深度遍历操作
 void DFSTraverse(Graph g)
 {
     for(int i=;i<=g.vexnum;i++){
         vis[i] = false;                        //初始化所有顶点状态都是未访问过状态
     }
     for(int i=;i<=g.vexnum;i++){
         if(!vis[i]){
             DFS(g,i);                        //对未访问的顶点调用DFS，若是连通图，只会执行一次
         }
     }
 }

 int main()
 {
     Graph g;
     createGraph(g);
     DFSTraverse(g);
     return ;
 }