Geodetic集合 c++

感谢某位不知名dalao的博客，我才知道怎么解题....

最开始连题意都读错了....这个故事告诉我们要好好读题

描述 Description
图G是一个无向连通图，没有自环，并且两点之间至多只有一条边。我们定义顶点v,u最短路径就是从v到u经过边最少的路径。所有包含在v-u的最短路径上的顶点被称为v-u的Geodetic顶点，这些顶点的集合记作I(v, u)。
我们称集合I(v, u)为一个Geodetic集合。
例如下图中，I(2, 5)={2, 3, 4, 5}，I(1, 5)={1, 3, 5}，I(2, 4)={2, 4}。

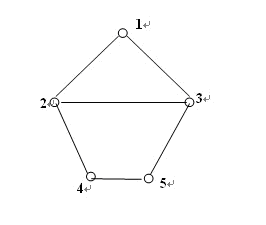
给定一个图G和若干点对v,u，请你分别求出I(v, u)。

输入格式 Input Format
第一行两个整数n,m，分别表示图G的顶点数和边数（顶点编号1-n）
　　下接m行，每行两个整数a,b表示顶点a和b之间有一条无向边。
　　第m+2行有一个整数k，表示给定的点对数。
　　下接k行，每行两个整数v,u。

输出格式 Output Format
　　共k行，每行对应输入文件中每一个点对v,u，按顶点编号升序输出I(v, u)。同一行的每个数之间用空格分隔。

样例输入 Sample Input
5 6
1 2
1 3
2 3
2 4
3 5
4 5
3
2 5
5 1
2 4

样例输出 Sample Output

2 3 4 5
1 3 5
2 4

思路挺简单，floyed一遍算出最短路径

然后再循环判断并记录集合内的点即可，然而实现看起来挺鬼畜！？感谢数据量不大吧.....

 #include<bits/stdc++.h>
 #define maxn 100
 using namespace std;
 struct node{
 　　int x,y;
 }a[];
 int n,m,kk;
 int fu[maxn][maxn],s[maxn][maxn];
 int dis[maxn][maxn][maxn];
 int main(){
 　　cin>>n>>m;
 　　memset(fu,,sizeof(fu));
 　　for(int i=;i<=n;i++)
 　　　　fu[i][i]=;
 　　for(int i=;i<=m;i++){
 　　　　int xx,yy;
 　　　　cin>>xx>>yy;
 　　　　fu[xx][yy]=;fu[yy][xx]=;
 　　}
 　　cin>>kk;
 　　for(int i=;i<=kk;i++){
 　　　　cin>>a[i].x>>a[i].y;
 　　}
 　　for(int k=;k<=n;k++)
 　　　　for(int i=;i<=n;i++)
 　　　　　　for(int j=;j<=n;j++)
 　　　　　　　　if(fu[i][k]+fu[k][j]<fu[i][j])//floyed求最短路
 　　　　　　　　　　fu[i][j]=fu[i][k]+fu[k][j];
 　　for(int k=;k<=n;k++)
 　　　　for(int i=;i<=n;i++)
 　　　　　　for(int j=;j<=n;j++)
 　　　　　　　　if(fu[i][k]+fu[k][j]==fu[i][j])//因为已经完成松弛，所以如果得出如此条件判断，说明是最短路径
 　　　　　　　　　　dis[i][j][++s[i][j]]=k;//i，j固定位置，数组s[i][j]记录经过点的个数，dis数组存储顶点
 　　for(int i=;i<=kk;i++){
 　　　　for(int j=;j<=s[a[i].x][a[i].y];j++)//枚举集合内的点的个数
 　　　　　　cout<<dis[a[i].x][a[i].y][j]<<' ';
 　　　　cout<<endl;
 　　}
 　　return ;
 }