拟牛顿法——DFP、BFGS、L-BFGS
DFP
该算法的核心是：通过迭代的方法，对Hk+1(-1)近似。迭代方式：
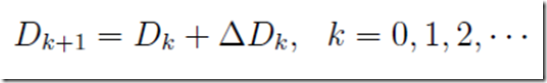
其中D0通常取为单位矩阵，关键是每一步构造矫正矩阵△Dk。
考虑△Dk 的待定形式为
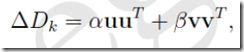
拟牛顿的条件
这里插播一下拟牛顿的条件。
前面有讲到，拟牛顿法是想找到一个近似矩阵D来近似海森矩阵H的逆。显然D的选择是必须有条件的。为了表示清楚，下文B≈H,D≈H-1
设经过k+1次迭代后得到Xk+1,此时将目标函数在Xk+1附近作泰勒展开，取二阶近似，得到
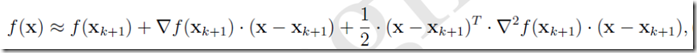
对其两边作用一个梯度算子▽，可得
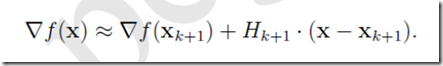
在上式中取X=Xk,并整理得到
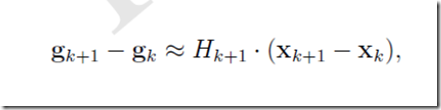
若引入记号
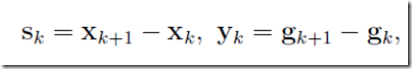
则有
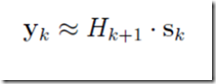或者
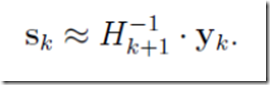
这就是所谓的拟牛顿条件对于我们的近似矩阵B或D则有
有了这个拟牛顿条件我们就能开始构造D了
构造矩阵D
结合两式：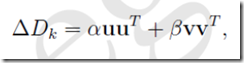
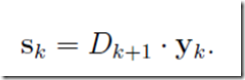
则有
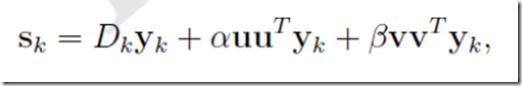
并且可以写成
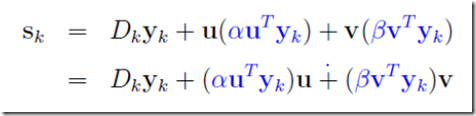
由于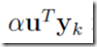
和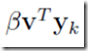
是两个数，且里面α和β在里面起到类似放缩的作用，不妨假设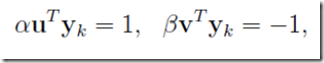
即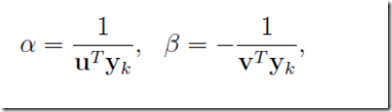
其中u，v仍是待定的
可以得到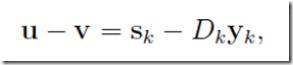
不妨直接取
则有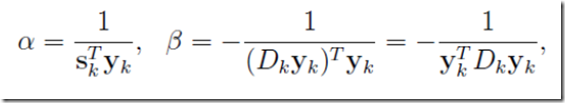
至此则有
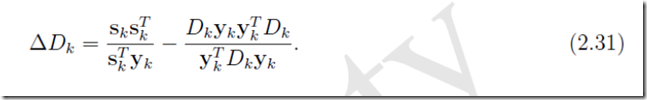
注：这里的（1.13）公式为
这里gk表示一阶导。
待更新！！
拟牛顿法——DFP、BFGS、L-BFGS的更多相关文章
- 牛顿法与拟牛顿法，DFP法，BFGS法，L-BFGS法
牛顿法 考虑如下无约束极小化问题: $$\min_{x} f(x)$$ 其中$x\in R^N$,并且假设$f(x)$为凸函数,二阶可微.当前点记为$x_k$,最优点记为$x^*$. 梯度下降法用的是 ...
- 牛顿法|阻尼牛顿法|拟牛顿法|DFP算法|BFGS算法|L-BFGS算法
一直记不住这些算法的推导,所以打算详细点写到博客中以后不记得就翻阅自己的笔记. 泰勒展开式 最初的泰勒展开式,若 在包含 的某开区间(a,b)内具有直到n+1阶的导数,则当x∈(a,b)时,有: ...
- 牛顿法/拟牛顿法/DFP/BFGS/L-BFGS算法
在<统计学习方法>这本书中,附录部分介绍了牛顿法在解决无约束优化问题中的应用和发展,强烈推荐一个优秀博客. https://blog.csdn.net/itplus/article/det ...
- 拟牛顿法/Quasi-Newton，DFP算法/Davidon-Fletcher-Powell，及BFGS算法/Broyden-Fletcher-Goldfarb-Shanno
拟牛顿法/Quasi-Newton,DFP算法/Davidon-Fletcher-Powell,及BFGS算法/Broyden-Fletcher-Goldfarb-Shanno 转载须注明出处:htt ...
- 最优化算法【牛顿法、拟牛顿法、BFGS算法】
一.牛顿法 对于优化函数\(f(x)\),在\(x_0\)处泰勒展开, \[f(x)=f(x_0)+f^{'}(x_0)(x-x_0)+o(\Delta x) \] 去其线性部分,忽略高阶无穷小,令\ ...
- 牛顿法与拟牛顿法学习笔记（四）BFGS 算法
机器学习算法中经常碰到非线性优化问题,如 Sparse Filtering 算法,其主要工作在于求解一个非线性极小化问题.在具体实现中,大多调用的是成熟的软件包做支撑,其中最常用的一个算法是 L-BF ...
- 牛顿法与拟牛顿法学习笔记（三）DFP 算法
机器学习算法中经常碰到非线性优化问题,如 Sparse Filtering 算法,其主要工作在于求解一个非线性极小化问题.在具体实现中,大多调用的是成熟的软件包做支撑,其中最常用的一个算法是 L-BF ...
- 牛顿法与拟牛顿法学习笔记（五）L-BFGS 算法
机器学习算法中经常碰到非线性优化问题,如 Sparse Filtering 算法,其主要工作在于求解一个非线性极小化问题.在具体实现中,大多调用的是成熟的软件包做支撑,其中最常用的一个算法是 L-BF ...
- <转>牛顿法与拟牛顿法
转自:http://blog.csdn.net/itplus/article/details/21896619 机器学习算法中经常碰到非线性优化问题,如 Sparse Filtering 算法,其主要 ...
随机推荐
- unity, UGUI Image shader
Image组件的Material成员默认是空,如果想为Image添加shader,只需新建material赋给Material即可. 另外注意,用于UI组件的shader都要包含一句:ZTest ...
- atitit.MIZIAN 陕北方言 特有词汇 大词典 attilax 整理 h--n v1 q31.xlsx
atitit.MIZIAN 陕北方言 特有词汇 大词典 attilax 整理 h--n v1 q31.xlsx 1 Mizian陕北方言 english英语 spain西班牙语 cantonese粤 ...
- Knockout JS 演示样例
五个小样例,来自Knockout JS官方站点. //tutorial 1 //following codes uses to demonstrate observable values and ta ...
- C++语言基础(1)-命名空间
一个中大型软件往往由多名程序员共同开发,会使用大量的变量和函数,当有两个人都同时定义了一个名字相同的全局变量或函数的时候,若是把他们的代码整合在一块编译,此时编译器就会提示变量或函数重复定义,C++为 ...
- 605. Can Place Flowers【easy】
605. Can Place Flowers[easy] Suppose you have a long flowerbed in which some of the plots are plante ...
- shell脚本之read工具
#!/bin/bash # -*- coding: utf-8 -*- # echo -n "please input your name: " read name echo &q ...
- UVA 1363 Joseph's Problem 找规律+推导 给定n,k;求k%[1,n]的和。
/** 题目:Joseph's Problem 链接:https://vjudge.net/problem/UVA-1363 题意:给定n,k;求k%[1,n]的和. 思路: 没想出来,看了lrj的想 ...
- PHPWord使用方法
官方文档 github地址 一.安装 直接使用composer安装,链接地址 composer require phpoffice/phpword 二.简单使用 require_once 'PhpO ...
- svn删除账户信息
当我们需要清理eclipse中记录的SVN账号信息时,按如下操作: eclipse中打开window------>preferences------->SVN页面,如下所示: 一般情况下, ...
- poj 2117(割点的应用)
题目链接:http://poj.org/problem?id=2117 思路:题目的意思是要求对于给定的无向图,删除某个顶点后,求最大的连通分量数.显然我们只有删掉割点后,连通分支数才会增加,因此我们 ...