【数据结构】最小生成树之prim算法和kruskal算法

在日常生活中解决问题经常需要考虑最优的问题，而最小生成树就是其中的一种。看了很多博客，先总结如下，只需要您20分钟的时间，就能完全理解。

比如：有四个村庄要修四条路，让村子能两两联系起来，这时就有最优的问题，怎样修才是做好的，如下图：第一个是网全图，后三个图的修路方案都可以

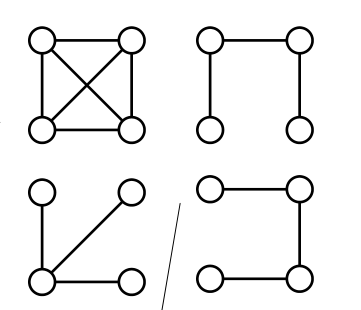
1.树的定义：有n个顶点和n-1条边，没有回路的称为树

生成树的定义：生成树就是包含全部顶点，n-1（n为顶点数）条边都在图里就是生成树

最小：指的是这些边加起来的权重之和最小

2.判定条件：向生成树中任加一条边都一定构成回路

充分必要条件：最小生成树存在那么图一定是连通的，反过来，图是连通的则最小生成树一定存在

3.和最小生成树有关的两个算法：prim算法和kruskal算法

a)prim算法——让小树慢慢长大型算法

按照树的定义，一个顶点就是一棵树。

原理：

1）我们选择一个顶点，也就是选择了一个树。

2）向外找权重最小的边，这样这棵树就有了两个顶点

3）再以这两个顶点向外找权重最小的边，依次循环，知道所有顶点收到树里

举例：

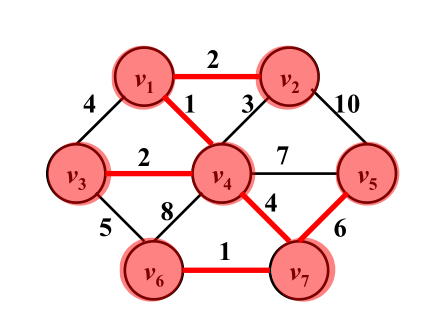
第一步：选择V1作为顶点

第二步：对比一下与V1相连的各条边的权重，选择最小的V1-V4这条边

第三步：以V1和V4为树，向外找权重最小的边，这时就有了V1-V2,V4-V3两条边，这样就把顶点V2和V3收进了树里。

接着以V1,V2,V3,V4为顶点的树，向外选权值最小的边，注意不能构成回路。依次循环，这样就选择了V4-V7,V7-V5,V7-V6这三条边

数一下现在已经包含了全部的7的顶点，和6条边了，这样最小生成树就长大了

b)kruskal算法——将森林合并为树

原理：

1）和prim算法不一样的是，kruskal算法先选择权重最小的边（因为一个顶点就是一棵树，那么一个边两个顶点就可以看成是一棵树）

2）接着选择剩下的权值比较小的边，注意不能形成回路，只到包含全部顶点

举例：

还是上面那幅图

第一步：先选择V1-V4,V6-V7两条权值为1的边

第二步：选择V4-V3,V1-V2两条权值为2的边。接着不能选择V4-V2权值为3的边，这样就构成了回路，只能选择V4-V7权值为4的边。

同理不能选择V6-V5权值为5的边，因为会构成回路，只能选择V7-V5权值为6的边。

此时就已经包含了全部的7的顶点，和6条边了，这样最小生成树就从森林变成了树