斯坦福机器学习视频笔记 Week4 & Week5 神经网络 Neural Networks

神经网络是一种受大脑工作原理启发的模式。 它在许多应用中广泛使用：当您的手机解释并理解您的语音命令时，很可能是神经网络正在帮助理解您的语音; 当您兑现支票时，自动读取数字的机器也使用神经网络。

Non-linear Classification

当输入数据特征过多，像上面的例子，当使用三次幂的特征时，可以超过170，000项，使我们的逻辑回归难以运行。

还有在计算机视觉中，图片的表示是通过像素矩阵表示的，如上图所示。那么假设一个图片是简单的50×50px，其特征数为2500（7500 if RGB），如果使用平方特征将达到百万级别，逻辑回归将无法适用。

Neurons and the brain

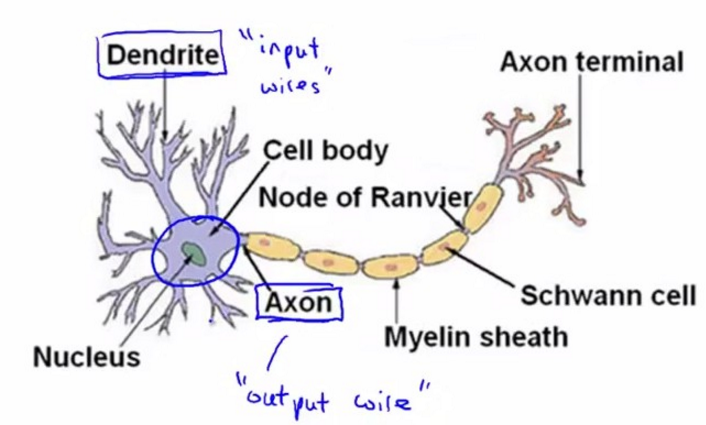
为模仿大脑的工作方式，神经网络可以类似的分为输入的数据特征，中间的数据处理层，和最后的输出。

Model Representation

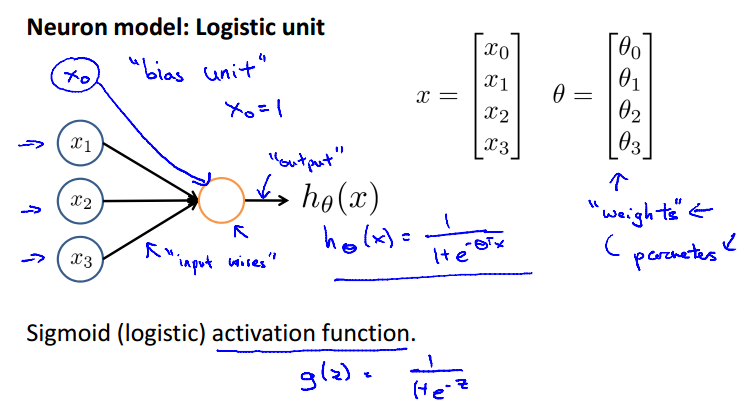
神经网络的简化形式如上图所示，x1，...xn为输入特征，输出为假设函数的结果。在模型中，通常会有一个额外的输入x0，我们称为"bias unit"（偏执单元），通常取值为1。

神经网络中我们依然使用逻辑回归中的逻辑函数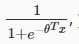，有时也称之为'sigmoid (logistic) activation function'。同时，那些参数theta也可以称为权值("weights")。

第一层为输入层（"input layer"），最后一层为输出层，输入层和输出层（"output layer"）之间的所有层统称为隐藏层（ "hidden" layer）。每一层的输入都可以增加一个偏执单元。

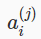=第j层的第i个激活结点（activation units.）

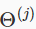=从第j层映射到j+1层的权重矩阵。

如果网络在第j层有Sj个单元（加上偏执单元），在j+1层有Sj+1个单元（不算偏执单元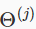），的维度将是。

如上面的例子，theta1=3×4，theta2=1×4。

Forward propagation: Vectorized implementation

为了将上面的神经网络的例子向量化，我们定义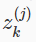表示逻辑函数g的参数。

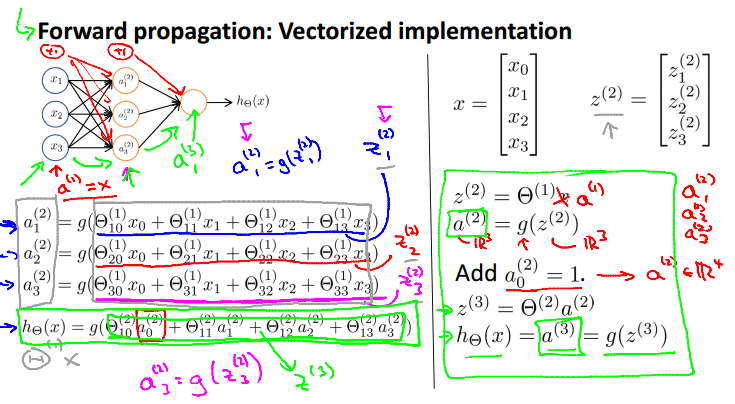
例如第2层的第k个结点表示如下：

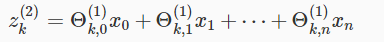
参数x和参数z向量化为：

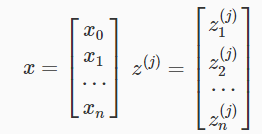
z相当于每一层的输入，而a相当于每一层的输出，z和激活结点a可以表示为：

，

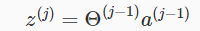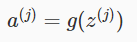
最后的输出为：

注意：请在每一层的输入加上偏执单元。

可以看出，我们在最后一步所做的和逻辑回归中其实是一样的。在网络中添加中间层目的是更好的处理复杂的非线性假设函数。

其实中间层数量可以是任意的，还有其他的网络结构。

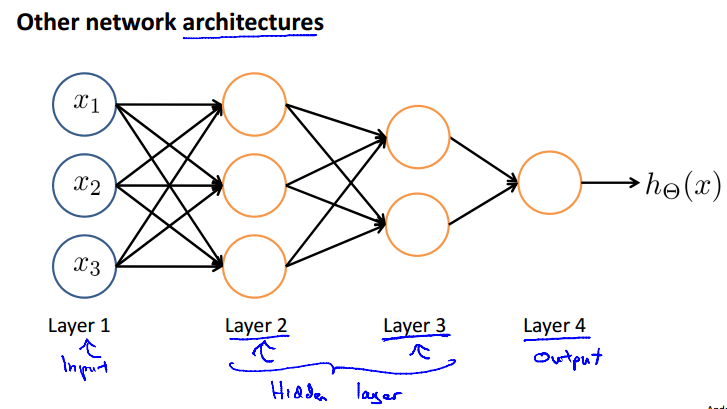
Examples and Intuitions

上面的例子实现了逻辑与。假设我们通过训练得到的theta={-30,20,20},将theta带入h（x）=g（-30+20x1+20x2），g（4.0）=0.99，g（-4.0）=0.01，由相应的函数值得到上面的真值表。

下面再给出一个例子实现逻辑或，训练得到的参数theta={-10,20,20}。

下面是一个更加复杂的例子，实现的是异或XNOR。

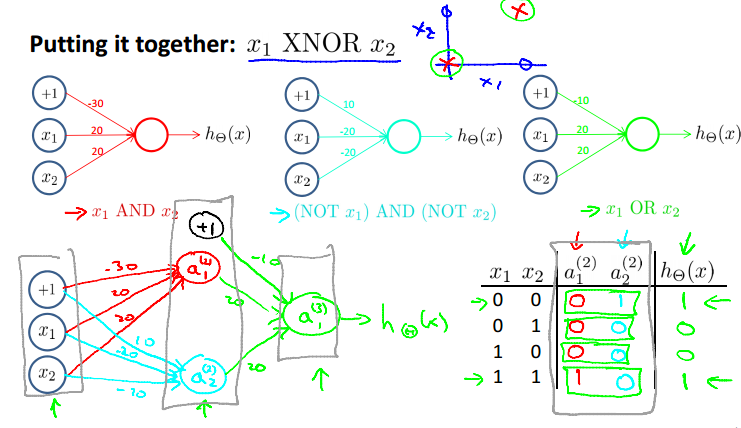
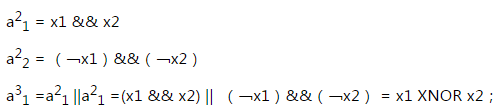
由上面的式子可得到上面的网络结构。

一个具体应用：手写数字识别。

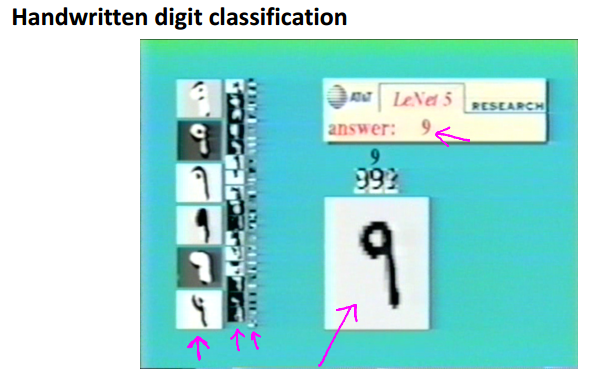
Multiclass Classification

为了实现多元分类，需要假设函数返回一个向量值。如上面的例子，每个输出单元代表一个特定分类，每一个输出向量只有一个分量可以为1，值为1的分量代表特定的分类。如上图中的，第一个输出为1 ，代表为行人，第二个为1代表小轿车，第三个为1代表摩托，第四个为1代表卡车。

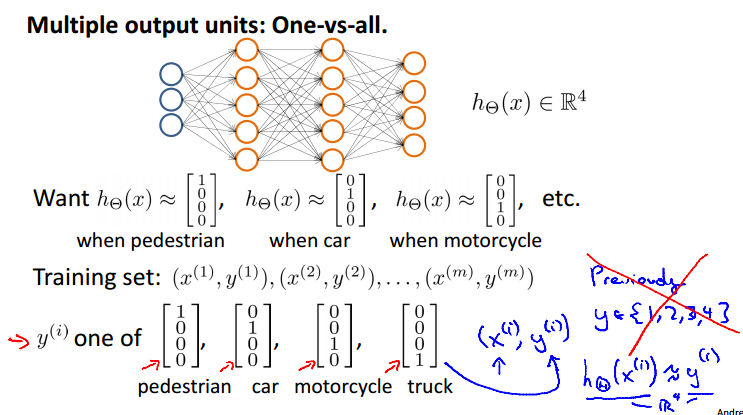
注：（假设函数h(theta)的输出为g(z)的函数值，并不是输出1和0，可能是0.01，0.99等数值）

分类结果集合可以为：

网络最后形式为：

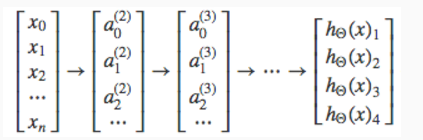
h（x）i表示第i类的预测函数。

Cost Function

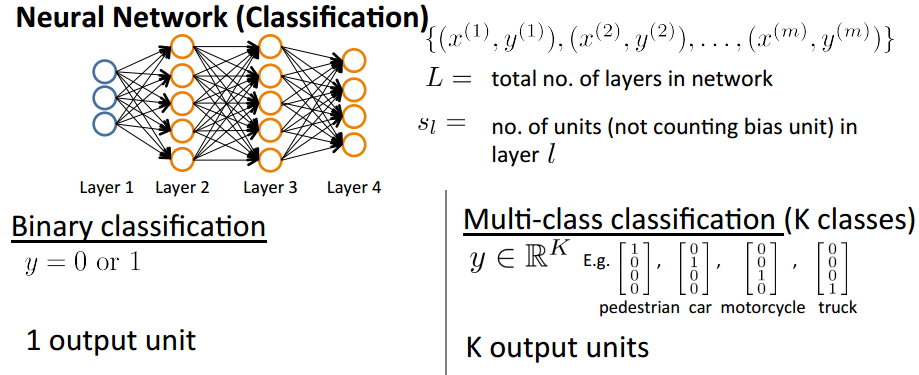
L:网络的总层数；

K：输出单元数；

Sl：l 层的单元数（不包括偏执单元）。

在二元分类中只需要一个输出单元，输出y={0,1}；在K元分类中，需要K个输出单元，输出为k维的向量（K > 2）。

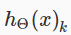对应第k类的假设函数，神经网络的cost function是逻辑回归的通用形式：

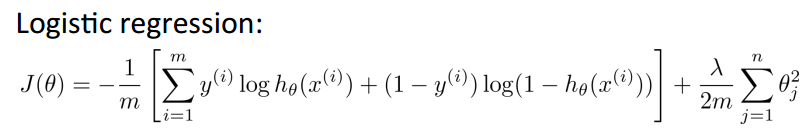
而我们即将使用的神经网络的cost function：

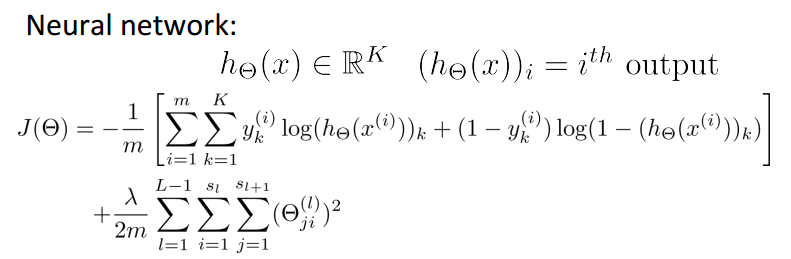
上面公式中，二层累加是对每个输出层单元计算损失值，三层累加是简单的累加网络中所有的theta参数平方值。

Backpropagation Algorithm

后向传播算法在神经网络中用来最小化我们的cost function，就像我们在线性回归和逻辑回归中使用梯度下降一样。

我们需要计算J（theta）和 J关于theta的偏导数。

为得到最优化的theta参数，我们进行如下操作。

首先我们只考虑一个训练数据（x，y）的情况。

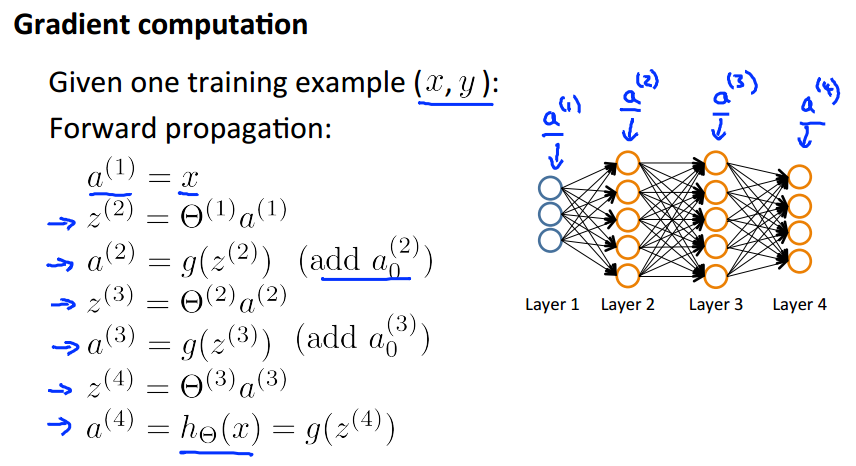
根据前向传播计算输出值，这个跟前面所讲的类似，具体例子和过程如上图所示。

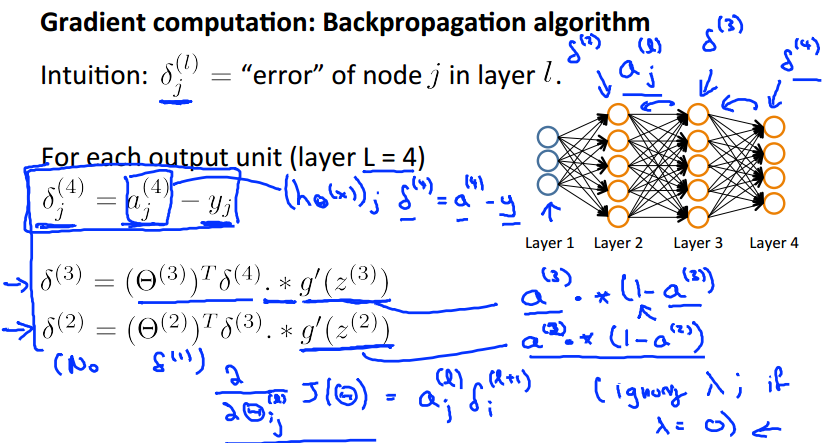
根据后向传播算法，计算J关于theta的偏导数。

定义：为第l层第j个结点的误差。

上面的例子，delta4 = a4 - y;可以看出隐藏层误差的计算有所不同，后面有

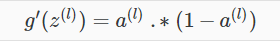
这样可以计算出J的偏导数：

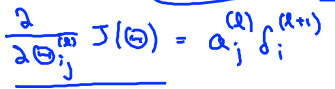
下面是完整的后向传播算法。

Δij用于计算J的偏导数，我还尚未知道其数学含义。我们还引入矩阵Dij以表示J（theta）的偏导数，考虑正则化时，j=0表示该结点为偏执结点（bais units），可以推导出右下角的公式。

下面通过一个例子来看看后向传播算法究竟在干什么。我们先忽略正则化，那cost function 将变成这样：

下面是具体的计算过程：

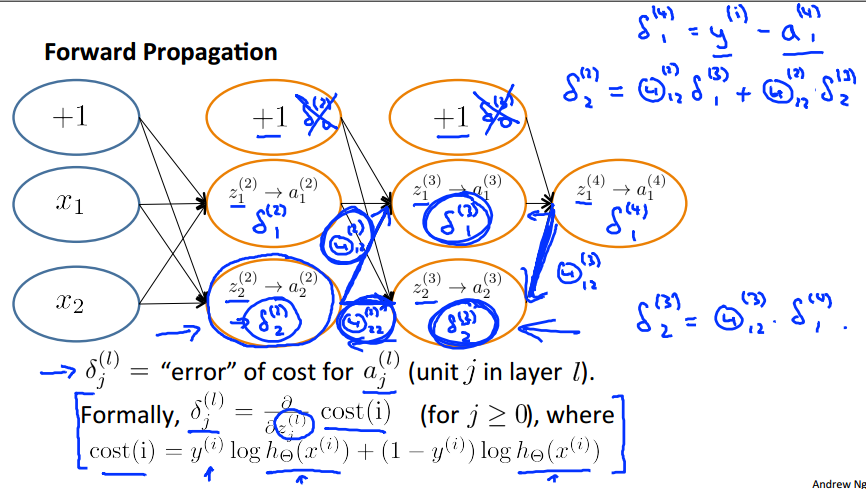
从左到右反向传播，低层的delta（l） = 高层的dealta（l+1）的加权求和，有公式：

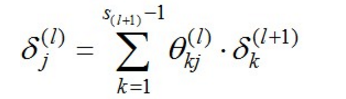
Implementation Note: Unrolling Parameters

在神经网络的训练中，我们需要处理大量的参数：

根据我们之前用octave实现线性回归和逻辑回归的经验，这里我们依然会使用优化函数例如 "fminunc()"，所以我们必须将这些参数变成“长长”的列向量，作为函数参数。

thetaVector = [ Theta1(:); Theta2(:); Theta3(:); ]
deltaVector = [ D1(:); D2(:); D3(:) ]

当我们要在函数中使用这些参数矩阵的时候，就可以再使用reshape，将它们还原。

Gradient Checking

神经网络的训练，不确定性很大，我们可以使用gradient checking来保证我们的代码正确的执行优化。下面就是其原理。

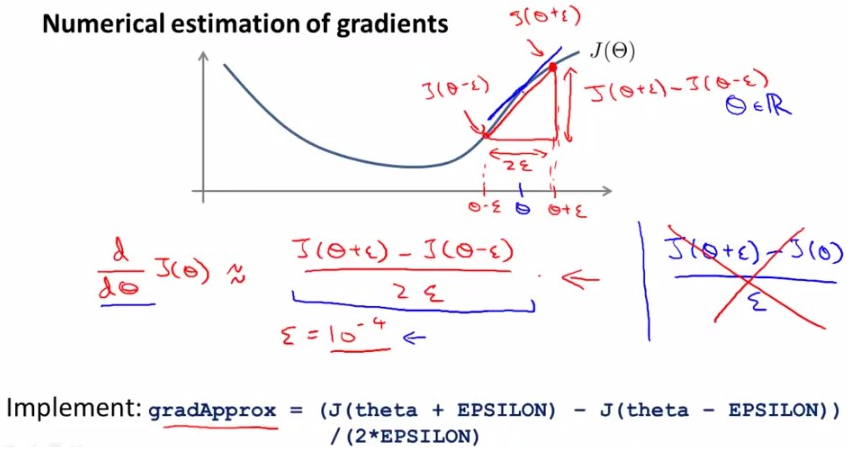
在点theta的两边，取(theta - epsilon) and (theta - epsilon) 计算这两点的正切值，作为J(theta)偏导数的近似值。回忆一下，导数的定义，我们知道这个值和J(theta)偏导数应该很接近的，所以这个方法是有效的。这个较小值epsilon通常取10的-4次方，如果太小程序可能出错。

对于每个参数的验证如下：

将我们得到的近似值，与我们得出的偏导数D做比较，如果相近，就说明程序运行正确，否则，程序运行错误。

注：如果gradient checking验证通过，则需要在以后的程序中关闭gradient checking，不然没迭代一次都要验证一次，程序会运行的很慢。

Random Initialization

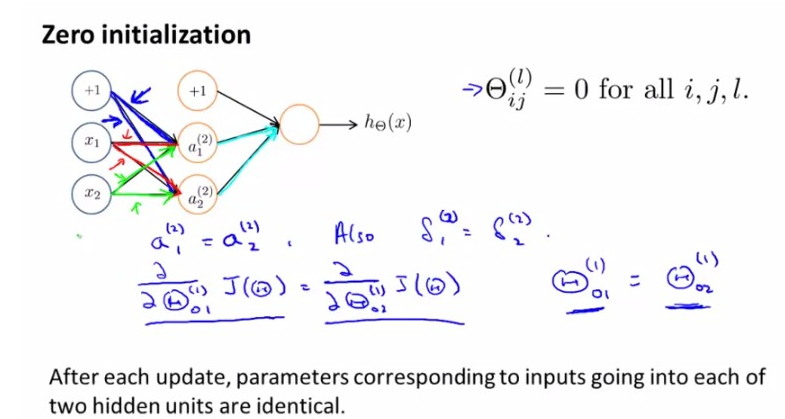
根据之前的经验，如果我们初始化所有参数theta为0，将得到一个类似单一重复的输入值，这将使算法的误差很大。

为了打破这种symmetry的状况，我们在[-ε,ε]范围内随机初始化这些theta，这样会达到很好的效果。

Putting It Together

最后将这些神经网络实现整理到一起：

最后想说的是，如果大家在实现神经网络作业有什么问题的时候，可以联系我qq：1208727315，我可以提供我的作业作为参考。

参考：http://blog.csdn.net/abcjennifer/article/details/7749309