AVL的旋转
转自http://blog.csdn.net/gabriel1026/article/details/6311339
平衡二叉树在进行插入操作的时候可能出现不平衡的情况,AVL树即是一种自平衡的二叉树,它通过旋转不平衡的节点来使二叉树重新保持平衡,并且查找、插入和删除操作在平均和最坏情况下时间复杂度都是O(log n)
AVL树的旋转一共有四种情形,注意所有旋转情况都是围绕着使得二叉树不平衡的第一个节点展开的。
1. LL型
平衡二叉树某一节点的左孩子的左子树上插入一个新的节点,使得该节点不再平衡。这时只需要把树向右旋转一次即可,如图所示,原A的左孩子B变为父结点,A变为其右孩子,而原B的右子树变为A的左子树,注意旋转之后Brh是A的左子树(图上忘在A于Brh之间标实线)
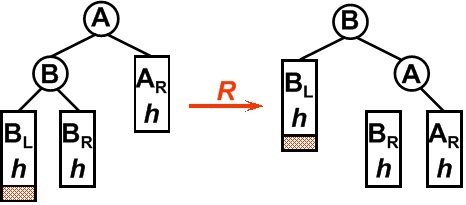
2. RR型
平衡二叉树某一节点的右孩子的右子树上插入一个新的节点,使得该节点不再平衡。这时只需要把树向左旋转一次即可,如图所示,原A右孩子B变为父结点,A变为其左孩子,而原B的左子树Blh将变为A的右子树。
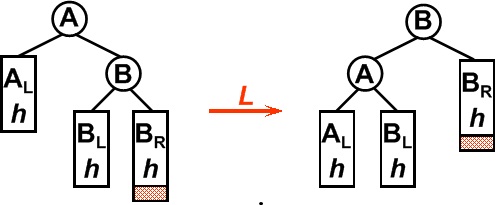
3. LR型
平衡二叉树某一节点的左孩子的右子树上插入一个新的节点,使得该节点不再平衡。这时需要旋转两次,仅一次的旋转是不能够使二叉树再次平衡。如图所示,在B节点按照RR型向左旋转一次之后,二叉树在A节点仍然不能保持平衡,这时还需要再向右旋转一次。
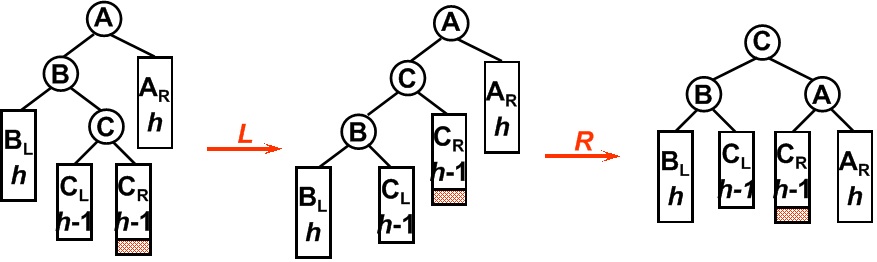
4. RL型
平衡二叉树某一节点的右孩子的左子树上插入一个新的节点,使得该节点不再平衡。同样,这时需要旋转两次,旋转方向刚好同LR型相反。
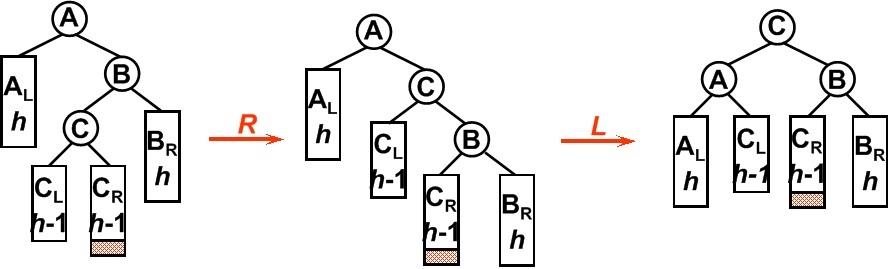
AVL的旋转的更多相关文章
- 我的新发现:AVL树旋转的一个特性
关于AVL树旋转的代码网络上铺天盖地. 一些经典的实现方法如下: AVLTree SingleLeftRotation(AVLTree A) { AVLTree B = A->left; A-& ...
- AVL树旋转
什么是AVL树? AVL树是带有平衡条件的二叉查找树,一颗AVL树首先是二叉查收树(每个节点如果有左子树或右子树,那么左子树中数据小于该节点数据,右子树数据大于该节点数据),其次,AVL树必须满足平衡 ...
- (精)AVL树旋转共8种情况(涵盖所有考研的范围)
- PAT树_层序遍历叶节点、中序建树后序输出、AVL树的根、二叉树路径存在性判定、奇妙的完全二叉搜索树、最小堆路径、文件路由
03-树1. List Leaves (25) Given a tree, you are supposed to list all the leaves in the order of top do ...
- AVL树的插入与删除
AVL 树要在插入和删除结点后保持平衡,旋转操作必不可少.关键是理解什么时候应该左旋.右旋和双旋.在Youtube上看到一位老师的视频对这个概念讲解得非常清楚,再结合算法书和网络的博文,记录如下. 1 ...
- 详解什么是平衡二叉树(AVL)(修订补充版)
详解什么是平衡二叉树(AVL)(修订补充版) 前言 Wiki:在计算机科学中,AVL树是最早被发明的自平衡二叉查找树.在AVL树中,任一节点对应的两棵子树的最大高度差为1,因此它也被称为高度平衡树.查 ...
- 什么是平衡二叉树(AVL)
前言 Wiki:在计算机科学中,AVL树是最早被发明的自平衡二叉查找树.在AVL树中,任一节点对应的两棵子树的最大高度差为1,因此它也被称为高度平衡树.查找.插入和删除在平均和最坏情况下的时间复杂度都 ...
- AVL树总结
定义:一棵AVL树或者是空树,或者是具有下列性质的二叉搜索树:它的左子树和右子树都是AVL树,且左右子树的高度之差的绝对值不超过1 AVL树失衡旋转总结: 假如以T为根的子树失衡.定义平衡因子为 H( ...
- AVL树(平衡二叉树)
定义及性质 AVL树:AVL树是一颗自平衡的二叉搜索树. AVL树具有以下性质: 根的左右子树的高度只差的绝对值不能超过1 根的左右子树都是 平衡二叉树(AVL树) 百度百科: 平衡二叉搜索树(Sel ...
随机推荐
- php发送get、post请求的几种方法
方法1: 用file_get_contents 以get方式获取内容 <?php $url='http://www.domain.com/'; $html = file_get_contents ...
- android studio 智能提示忽略大小写
Step1: Step2:
- CSDN——【低调的草原狼】——Ext4.2学习目录整理
最近在研究ExtJS,发现CSDN中有个博客中一系列文档非常优秀,但是没有对目录进行整理,在此稍作整理,也为以后自己研究打下一个基础: 原文作者:低调的草原狼 目录: 1.ExtJS4.2学习 ...
- javascript数学计算
◎Math.ceil()执行向上舍入,即它总是将数值向上舍入为最接近的整数:◎Math.floor()执行向下舍入,即它总是将数值向下舍入为最接近的整数:◎Math.round()执行标准舍入,即它总 ...
- PrintQueue
PrintQueueCollection printQueues = null; var printServer = new PrintServer(); printQueues = printSer ...
- Emmet快速编写CSS样式
基本的CSS样式编写时,很多样式只需输入首字母即可得到不带属性值的CSS样式,像上面说到的margin. 1.而对于一些带有特定的属性值的CSS样式,只需输入CSS标签与属性值的首字母就可以,比如: ...
- Java基于Socket文件传输示例(转)
最近需要进行网络传输大文件,于是对基于socket的文件传输作了一个初步的了解.在一位网友提供的程序基础上,俺进行了一些加工,采用了缓冲输入/输出流来包装输出流,再采用数据输入/输出输出流进行包装,加 ...
- EasyTouch 3.1中文翻译
Unity3D的Easy Touch 的手册最近寻找中文版本,google无果,自己动手.目前暂时只有c# ,javascript原理是一样的. 一.Quick Start 1-Import Easy ...
- How does database indexing work?
When data is stored on disk based storage devices, it is stored as blocks of data. These blocks are ...
- 在实体注解OneToMany时,要加上mappedby,避免产生中间表。
在实体注解OneToMany时,要加上mappedby,避免产生中间表.
