POJ 3377 Ferry Lanes

虽然它出现在dp专场里···但是我第一反应是一道最短路题···不过幸好它出现在dp专场里···因为我不怎么会dijstra什么的···

题意：一条河上有N+1对码头，每个相邻码头之间需要一定时间到达，每对码头之间也需要一定时间到达，如下图：

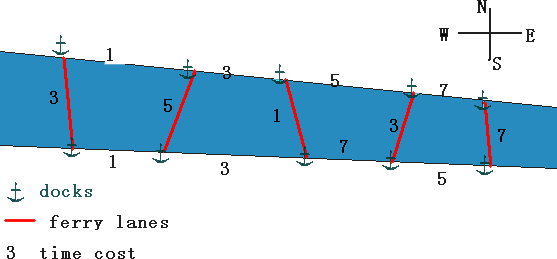
给出起点码头和终点码头，问最短到达时间。

解法：假设起点码头一定在左边，终点码头一定在右边，那么为了时间最短一定是向右或向上（下）走，所以dp数组为每个从起点出发到每个码头时的最短耗时，dp方程很好确定，但是上下码头的顺序无法确定，而当路径是由对面码头过来的时候，对面码头的dp值一定不是从当前码头而来，dp方程dp[0][i] = min(dp[0][i - 1] + time[0][i - 1], dp[1][i - 1] + time[1][i - 1] + time[2][i]),dp[1][i]
= min(dp[1][i - 1] + time[1][i - 1], dp[0][i - 1] + time[0][i - 1] + time[2][i])。

但从起点（终点）到它对面的时间需要另外处理，例如如下情况：

显然从南方的码头出发向右绕一圈后所需时间较短，所以要分别对起点通过左面路径到达对面码头的最短时间和终点通过右面路径到达对面码头的最短时间进行处理，绕行走的一定是U形路，所以只要计算所有U形路的最小时间，不过我还是用的dp写的···不是很好理解···

对于终点的绕行时间在最后要特殊处理，因为绕行时间和中间路径的dp过程有矛盾的地方。

一开始TLE了···但是我听说了某喵的惨痛经历后把memset改掉之后1900msA掉了···郁闷

代码：

#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<string>
#include<string.h>
#include<math.h>
#include<limits.h>
#include<time.h>
#include<stdlib.h>
#include<map>
#include<queue>
#include<set>
#include<stack>
#include<vector>
#define LL long long
using namespace std;
struct node
{
    long long num;
    int dir;
};
long long dp[2][1000005];
long long c[3][1000005];
int main()
{
    int n;
    while(~scanf("%d", &n) && n)
    {
        for(int i = 0; i < 2; i++)
            for(int j = 0; j < 1000005; j++)
                dp[i][j] = -1;
        //memset(dp, -1, sizeof(dp));
        node st, fi;
        scanf("%d%lld%d%lld", &st.dir, &st.num, &fi.dir, &fi.num);
        if(st.num > fi.num)
        {
            node tmp = st;
            st = fi;
            fi = tmp;
        }
        dp[st.dir][st.num] = 0;
        dp[fi.dir][fi.num] = 0;
        for(int i = 0; i < n; i++)
            scanf("%lld", &c[0][i]);
        for(int i = 0; i <= n; i++)
            scanf("%lld", &c[2][i]);
        for(int i = 0; i < n; i++)
            scanf("%lld", &c[1][i]);
        for(int i = st.num - 1; i >= 0; i--)
            dp[st.dir][i] = c[st.dir][i] + dp[st.dir][i + 1];
        dp[!st.dir][0] = c[2][0] + dp[st.dir][0];
        for(int i = 1; i <= st.num; i++)
            dp[!st.dir][i] = min(dp[st.dir][i] + c[2][i], dp[!st.dir][i - 1] + c[!st.dir][i - 1]);
        for(int i = fi.num + 1; i <= n; i++)
            dp[fi.dir][i] = c[fi.dir][i - 1] + dp[fi.dir][i - 1];
        dp[!fi.dir][n] = c[2][n] + dp[fi.dir][n];
        for(int i = n - 1; i >= fi.num; i--)
            dp[!fi.dir][i] = min(dp[fi.dir][i] + c[2][i], dp[!fi.dir][i + 1] + c[!fi.dir][i]);
        for(int i = st.num + 1; i < fi.num; i++)
        {
            dp[0][i] = min(dp[0][i - 1] + c[0][i - 1], dp[1][i - 1] + c[1][i - 1] + c[2][i]);
            dp[1][i] = min(dp[1][i - 1] + c[1][i - 1], dp[0][i - 1] + c[0][i - 1] + c[2][i]);
        }
        if(fi.num > 0)
        {
            dp[!fi.dir][fi.num] += dp[!fi.dir][fi.num - 1] + c[!fi.dir][fi.num - 1];
            dp[fi.dir][fi.num] = min(dp[!fi.dir][fi.num], dp[fi.dir][fi.num - 1] + c[fi.dir][fi.num - 1]);
        }
        else
            dp[fi.dir][fi.num] = dp[!fi.dir][fi.num];
        cout << dp[fi.dir][fi.num] << endl;
    }
    return 0;
}

不想写注释了···就算写了我的代码也不会变的好读的QAQ

_(:з」∠)_