后缀数组(suffix array)详解

写在前面

在字符串处理当中，后缀树和后缀数组都是非常有力的工具。

其中后缀树大家了解得比较多，关于后缀数组则很少见于国内的资料。

其实后缀数组是后缀树的一个非常精巧的替代品，它比后缀树容易编程实现，

能够实现后缀树的很多功能而时间复杂度也不太逊色，并且，它比后缀树所占用的空间小很多。

可以说，在信息学竞赛中后缀数组比后缀树要更为实用！

因此在本文中笔者想介绍一下后缀数组的基本概念、构造方法，

以及配合后缀数组的最长公共前缀数组的构造方法，最后结合一些例子谈谈后缀数组的应用。

What Is Suffix Array?

学习后缀数组需要认识几个概念：

子串

　　字符串S的子串r[i..j]，i<=j，表示S串中从i到j这一段，就是顺次排列r[i],r[i+1],...,r[j]形成的子串。

后缀

　　后缀是指从某个位置 i 开始到整个串末尾结束的一个特殊子串。字符串r的从第i个字符开始的后缀表示为Suffix(i)，

也就是Suffix(i)=S[i...len(S)-1] 。

后缀数组(SA[i]存放排名第i大的后缀首字符下标)

　　后缀数组 SA 是一个一维数组，它保存1..n 的某个排列SA[1] ，SA[2] ，...,SA[n] ，

　　并且保证Suffix(SA[i])<Suffix(SA[i+1])， 1<=i<n 。

也就是将S的n个后缀从小到大进行排序之后把排好序的后缀的开头位置顺次放入SA 中。

名次数组（rank[i]存放suffix(i)的优先级）

　　名次数组 Rank[i] 保存的是 Suffix(i) 在所有后缀中从小到大排列的“名次”

　　注：这个是排序的关键字~（这句话是我们排序的重点）

(我的理解):

sa[i]:保存的是S字符串的所有后缀在以字典序排序后，排在第i名的字符串在原来子串中的位置。

rank[i]:保存的是S字符串的所有后缀在以字典序排序后，原来的第i名现在排第几。

简单的说，后缀数组（SA）是“排第几的是谁？”，名次数组（RANK）是“你排第几？”。

容易看出，后缀数组和名次数组为互逆运算。我们只要算出了sa数组，就可以在O(n)的时间复杂度内算出rank数组。

height数组：height[i]保存的是suffix(i)和suffix(i-1)的最长公共前缀的长度。也就是排名相邻的两个后缀的最长公共前缀。

How To Build Suffix Array?

要构造Suffix Array,主要就是构造sa数组,rank数组和height数组。

首先来看一下如何构造sa数组：

构造sa数组的方法有三种：

1)倍增算法：O(nlongn)

2)DC3算法：O(n)

3)skew算法(不常用)

这里主要讲一下DC3算法：

DC3算法是一个优秀的线性算法！

很多人都认为DC3算法很复杂，其实也没多复杂，代码也就40多行，只是for循环多了点。

DC3算法：

1) 先将后缀分成两部分，然后对第一部分的后缀排序。

　　字符的编号从0开始。

　　将后缀分成两部分：

　　　　第一部分是后缀k（k模3不等于0）

　　　　第二部分是后缀k（k模3等于0）

2) 利用（1）的结果，对第二部分的后缀排序。
3) 将（1）和（2）的结果合并，即完成对所有后缀排序。

于是求出了所有后缀的排序，有什么用呢？主要是用于求它们之间的最长公共前缀（Longest Common Prefix，LCP）。

求出sa数组之后，根据rank[sa[i]]=i，rank数组自然也就能够在O(n)的时间内求出。

那我们如何快速的求出height数组呢？

令LCP(i,j)为第i小的后缀和第j小的后缀（也就是Suffix(SA[i])和Suffix(SA[j])）的最长公共前缀的长度，则有如下两个性质：

对任意i<=k<=j，有LCP(i,j) = min(LCP(i,k),LCP(k,j))
LCP(i,j)=min(i<k<=j)(LCP(k-1,k))

令height[i]＝LCP(i-1,i)，即height[i]代表第i小的后缀与第i-1小的后缀的LCP，则求LCP(i,j)就等于求height[i+1]~height[j]之间的RMQ，套用RMQ算法就可以了，复杂度是预处理O(nlogn)，查询O(1).

这样一来我们就将height数组也求出来了。

下面用草稿纸来模拟一遍：

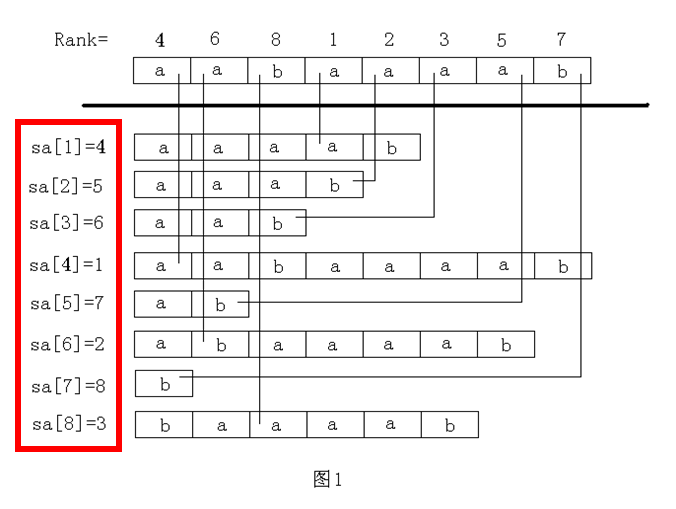
例如：
aabaaaab

总共有n=8个后缀：

1: aabaaaab

2: abaaaab

3: baaaab

4: aaaab

5: aaab

6: aab

7: ab

8: b

按照字典序排序后

sa[ 1 ] = 4 aaaab
sa[ 2 ] = 5 aaab
sa[ 3 ] = 6 aab
sa[ 4 ] = 1 aabaaaab
sa[ 5 ] = 7 ab
sa[ 6 ] = 2 abaaaab
sa[ 7 ] = 8 b
sa[ 8 ] = 3 baaaab

rank数组为：
rank[1]=4
rank[2]=6
rank[3]=8
rank[4]=1
rank[5]=2
rank[6]=3
rank[7]=5
rank[8]=7

height数组为：

height[ 1 ]=null
height[ 2 ]= 3
height[ 3 ]= 2
height[ 4 ]= 3
height[ 5 ]= 1
height[ 6 ]= 2
height[ 7 ]= 0
height[ 8 ]= 1

因此，所有子串的最长公共子串就是3.

这里给出一个理解程序：

/*

* this code is made by crazyacking

* Verdict: Accepted

* Submission Date: 2015-05-09-21.22

* Time: 0MS

* Memory: 137KB

*/

#include <queue>

#include <cstdio>

#include <set>

#include <string>

#include <stack>

#include <cmath>

#include <climits>

#include <map>

#include <cstdlib>

#include <iostream>

#include <vector>

#include <algorithm>

#include <cstring>

#define  LL long long

#define  ULL unsigned long long

using namespace std;

const int MAXN=;

//以下为倍增算法求后缀数组

int wa[MAXN],wb[MAXN],wv[MAXN],Ws[MAXN];

int cmp(int *r,int a,int b,int l)

{return r[a]==r[b]&&r[a+l]==r[b+l];}

/**< 传入参数：str,sa,len+1,ASCII_MAX+1 */

void da(const char *r,int *sa,int n,int m)

{

      int i,j,p,*x=wa,*y=wb,*t;

      for(i=; i<m; i++) Ws[i]=;

      for(i=; i<n; i++) Ws[x[i]=r[i]]++;

      for(i=; i<m; i++) Ws[i]+=Ws[i-];

      for(i=n-; i>=; i--) sa[--Ws[x[i]]]=i;

      for(j=,p=; p<n; j*=,m=p)

      {

            for(p=,i=n-j; i<n; i++) y[p++]=i;

            for(i=; i<n; i++) if(sa[i]>=j) y[p++]=sa[i]-j;

            for(i=; i<n; i++) wv[i]=x[y[i]];

            for(i=; i<m; i++) Ws[i]=;

            for(i=; i<n; i++) Ws[wv[i]]++;

            for(i=; i<m; i++) Ws[i]+=Ws[i-];

            for(i=n-; i>=; i--) sa[--Ws[wv[i]]]=y[i];

            for(t=x,x=y,y=t,p=,x[sa[]]=,i=; i<n; i++)

                  x[sa[i]]=cmp(y,sa[i-],sa[i],j)?p-:p++;

      }

      return;

}

int sa[MAXN],Rank[MAXN],height[MAXN];

//求height数组

/**< str,sa,len */

void calheight(const char *r,int *sa,int n)

{

      int i,j,k=;

      for(i=; i<=n; i++) Rank[sa[i]]=i;

      for(i=; i<n; height[Rank[i++]]=k)

            for(k?k--:,j=sa[Rank[i]-]; r[i+k]==r[j+k]; k++);

      // Unified

      for(int i=n;i>=;--i) ++sa[i],Rank[i]=Rank[i-];

}

char str[MAXN];

int main()

{

      while(scanf("%s",str)!=EOF)

      {

            int len=strlen(str);

            da(str,sa,len+,);

            calheight(str,sa,len);

            puts("--------------All Suffix--------------");

            for(int i=; i<=len; ++i)

            {

                  printf("%d:\t",i);

                  for(int j=i-; j<len; ++j)

                        printf("%c",str[j]);

                  puts("");

            }

            puts("");

            puts("-------------After sort---------------");

            for(int i=; i<=len; ++i)

            {

                  printf("sa[%2d ] = %2d\t",i,sa[i]);

                  for(int j=sa[i]-; j<len; ++j)

                        printf("%c",str[j]);

                  puts("");

            }

            puts("");

            puts("---------------Height-----------------");

            for(int i=; i<=len; ++i)

                  printf("height[%2d ]=%2d \n",i,height[i]);

            puts("");

            puts("----------------Rank------------------");

            for(int i=; i<=len; ++i)

                  printf("Rank[%2d ] = %2d\n",i,Rank[i]);

            puts("------------------END-----------------");

      }

      return ;

}

The Use Of Suffix Array

这里只是简单的介绍几种后缀数组的运用，真正的熟练后缀数组，还需要通过不断的做题、不断的实践来掌握。

最长公共子串

我们知道，字符串的任何一个子串都可以看作是这个字符串某个的后缀的前缀。
求A和B的最长公共子串等价于求A的后缀和B的后缀的最长公共前缀的最大值。
将第二个字符串写在第一个字符串的后面，中间用一个没有出现过的字符隔开，在求出这个新字符串的后缀数组，然后我们只需要找最大的height[i]就可(前提是要判断是否不在同一个字符串中)。
单个字符串的相关问题
两个字符串的相关问题
多个字符串的相关问题