题解 [USACO18DEC]Balance Beam

被概率冲昏的头脑~~~

我们先将样例在图上画下来：

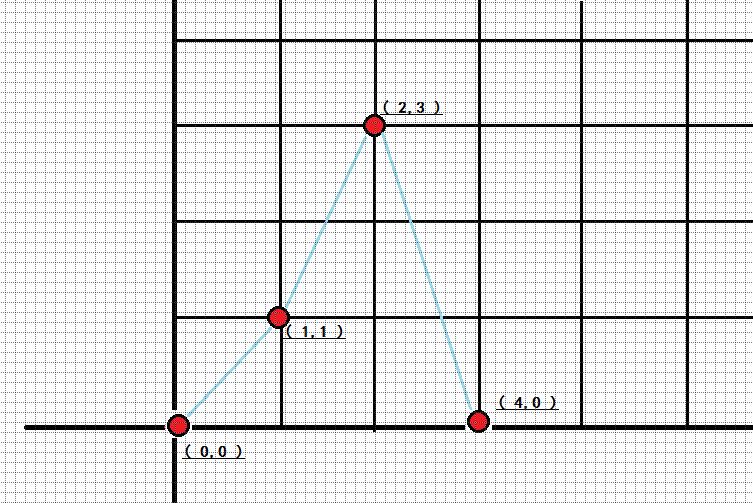
会发现，最大收益是：

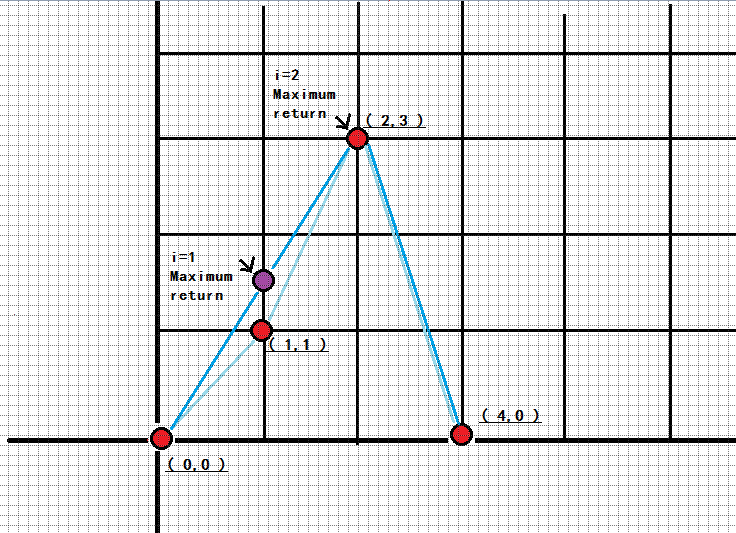
看出什么了吗？

这不就是凸包吗？

跑一遍凸包就好了呀，这些点中，如果i号点是凸包上的点，那么它的ans就是自己(第二个点)，不然的话，从上图来看，i的ans肯定和他相邻的两个是凸包边界的点有关(0节点和2节点)，那么怎么求这个ans呢？(第x号点为横坐标为x的点)

实际上我也不知道就是个期望公式啊!

l[i]记录i号点往左走第一个为凸包边界的点(如果i为1号，那么l[i]为0，特殊的，如果i为2号，那么l[i]就是本身)，r[i]同理。当l[x]==r[x]时，x时边界。

就是这个方程： (f[l[i]])*(r[i]-i)+f[r[i]]*(i-l[i])))/(r[i]-l[i]);

基础的期望方程，在此不再赘述(实际上是不会证)

关于凸包，在这贴一波yyb大神的博客：传送门戳我QwQ(顺便膜一波yyb大神%%%)

#include<bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define RI register int
#define F 100000
using namespace std;
const int NS=1e5+5;
ll f[NS],l[NS],r[NS],hep[NS];
//f如题,l[i]/r[i]如上文,hep为凸包
template <typename _Tp> inline void IN(_Tp&x){
	char ch;bool flag=0;x=0;
	while(ch=getchar(),!isdigit(ch))if(ch=='-')flag=1;
	while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
	if(flag)x=-x;
}
int main(){
    int n,top=0;IN(n);hep[++top]=0;//注意先加入0!
    for(int i=1;i<=n;++i)IN(f[i]);
	for(int i=1;i<=n+1;++i){//凸包
		while(top>=2){
			int a=hep[top],b=hep[top-1];
			if(((f[a]-f[b])*(i-a))<((f[i]-f[a])*(a-b)))--top;
			else break;
		}hep[++top]=i;
	}
	for(int i=1;i<top;++i){
		//中间的节点的l,r值都为hep[i]/hep[i+1]
		for(int j=hep[i]+1;j<hep[i+1];++j){
			l[j]=hep[i],r[j]=hep[i+1];
		}l[hep[i]]=hep[i],r[hep[i]]=hep[i];
	}
	for(int i=1;i<=n;++i){
		ll ans=0;//记得LL!
		if(l[i]==r[i])ans=f[i]*F;//为边界，直接跳下最优
		else ans=(F*(f[l[i]]*(r[i]-i)+f[r[i]]*(i-l[i])))/(r[i]-l[i]);//否则用方程算
		printf("%lld\n",ans);
	}return 0;
}