UVA-1599 Ideal Path（双向BFS）

题目：

给一个n个点m条边（2≤m≤100000, 1≤m≤200000）的无向图，每条边上都涂有一种颜色（用1到1000000000表示）。求从结点1到结点n的一条路径，

使得经过的边数尽量少，在此前提下，经过边的颜色序列的字典序最小。一对结点间可能有多条边，一条边可能连接两个相同结点。输入保证结点1可以

到达结点n。

思路：

看到边数尽量少，颜色序列字典序最小，知道这是用BFS来做这个题。但是一直卡在怎么处理颜色的字典序最小上。看了答案之后知道先逆向处理每个节点到终点

的距离d[ i ]，然后在正向分层BFS找出颜色最小的一条路径。

1.逆向处理距离d[]数组。

2.正向分层BFS根据当前结点的d[i]与下一个结点的d[i+1]之间差1来得出颜色字典序最小的一条路径。

这里我一开始使用队列来写的，但是这种写法在一层中找最小的颜色的时候是只找了一个结点，这就导致了得出的答案中的颜色不一定是同一条路径上的。

例如下面这个例子：

6 6
1 2 1
1 3 1
2 4 3
3 5 2
4 6 4
5 6 5

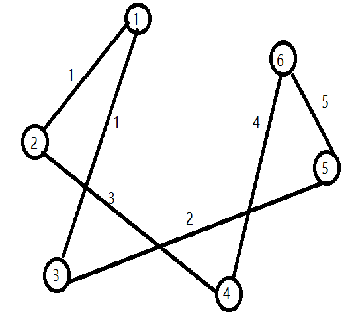
正确的答案应该是1,2,5，而我写出的答案却是1,2,4，苦思无果到网上看了下大佬的博客自己才写出来。

既然是分层BFS那么这种情况我们可以用循环遍历每一层，在每一层中用一个vector数组来存一下这一层中的所有的节点，

在这些节点中查找最小的颜色，然后处理这个最小颜色下面的边连接的点，更新这个vector数组知道结束。

代码：

#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define MAX 1000000009
#define FRE() freopen("in.txt","r",stdin)
#define FRO() freopen("out.txt","w",stdout)
using namespace std;
typedef long long ll;
const int maxn = ;
int n,m,d[maxn],vis[maxn];
struct Edge {
    int to,color;
    Edge(int to,int color) {
        this->to = to;
        this->color = color;
    }
};
vector<Edge>mp[maxn];

void BFS_reverse() {//逆向简单的BFS求最短路径。各个边的权值为1
    memset(vis,,sizeof(vis));
    d[n] = ;
    vis[n] = ;
    queue<int> que;
    que.push(n);
    while(!que.empty()) {
        int u = que.front();
        que.pop();
        for(int i = ; i<mp[u].size(); i++) {
            Edge e = mp[u][i];
            if(vis[e.to]==) {
                vis[e.to] = ;
                d[e.to] = d[u]+;
                que.push(e.to);
            }
        }
    }
}

void BFS() {
    memset(vis,,sizeof(vis));
    vector<int> next;
    next.push_back();
    vector<int> ans;
    for(int k = ; k<d[]; k++) {//遍历这个图中所有的层次
        int mmin = MAX;

        for(int i=; i<next.size(); i++) {//从这一层中的所有的节点中找到最小的颜色
            int u = next[i];
            for(int j=; j<mp[u].size(); j++) {
                Edge e = mp[u][j];
                if(d[e.to]+==d[u]) {
                    mmin = min(mmin, e.color);
                }
            }
        }

        ans.push_back(mmin);//将答案颜色保存
        vector<int> temp;

        for(int i=; i<next.size(); i++) {//保存与最小颜色连接且处于下一层的结点
            int u = next[i];
            for(int j=; j<mp[u].size(); j++) {
                Edge e = mp[u][j];
                if(d[u]==d[e.to]+ && vis[e.to]== && e.color==mmin) {
                    temp.push_back(e.to);
                    vis[e.to] = ;
                }
            }
        }
        next = temp;//更新next数组
    }
    printf("%d\n",ans.size());
    printf("%d",ans[]);
    for(int i=; i<ans.size(); i++) {
        printf(" %d",ans[i]);
    }
    printf("\n");
    return;
}

int main() {
    //FRE();
    //FRO();
    while(scanf("%d%d",&n,&m)!=EOF) {
        memset(d,,sizeof(d));
        for(int i=; i<*n; i++) {//一定要注意这里的范围，一晚上找错误就卡死在这里了
            mp[i].clear();
        }
        for(int i = ; i<m; i++) {
            int st,en,color;
            scanf("%d%d%d",&st,&en,&color);
            mp[st].push_back(Edge(en,color));
            mp[en].push_back(Edge(st,color));
        }
        BFS_reverse();
        BFS();
    }
    return ;
}