Luogu2261[CQOI2007]余数求和 【数论】By cellur925

题目传送门

省选题竟然送了这么多分，60分直接暴力算就行。（算了，07年的省选）

数学题嘛，通常我们需要把式子展开，然后寻找一些性质化简=w=。

展开式以及寻找规律的过程lyd老师讲的很清楚T_T，放照片了...

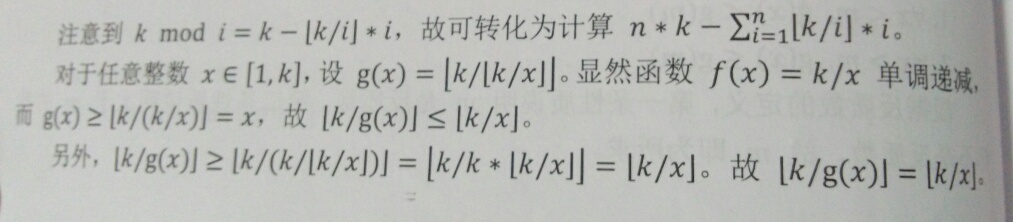
如果不能冷静分析，理论证明，我们还可以打表呀

一位dalao的打表法

发现了k/i在一定范围内是相等的后，我们就可以降低复杂度了，x是我们当前到的i（增强了效率），gu是相同值组成的块的右端点，之后我们就可以用等差数列算出sigma下标，问题得解。这也是除法分块的一个方法技巧。

细节：防止整数被0处，特判一下。

Code

 #include<cstdio>
 #include<algorithm>

 using namespace std;
 typedef long long ll;

 int gu;
 ll n,k,ans;

 int main()
 {
     scanf("%lld%lld",&n,&k);
     ans=n*k;
     for(int x=;x<=n;x=gu+)
     {
         gu=k/x ? min(k/(k/x),n) : n;
         ans-=(k/x)*(x+gu)*(gu-x+)>>;
     }
     printf("%lld",ans);
     return ;
 }