HackerRank# Hexagonal Grid

原题地址

铺瓷砖的变种，做法也是类似

假设地板长下面这样，灰色的是无法填充的空洞，初始时可以把N块之外的地板填充成灰色的，便于边界处理

假设现在从后向前已经处理完了一部分，绿色的砖块代表已经遍历过了，蓝色虚线框代表已经计算完成的子问题

现在要遍历红色边框的地砖

只可能有两种铺法：

如果可以向下铺，很简单，递推到另一个子问题

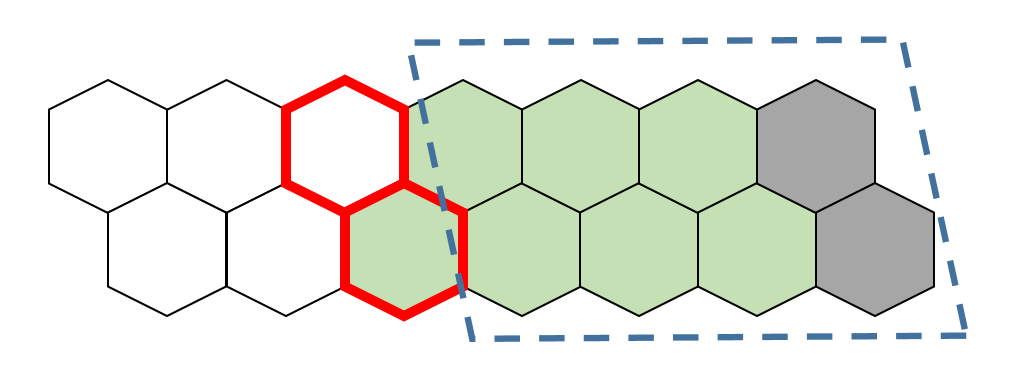
如果向右铺，就有些麻烦了，又两种可能

第一种可能，有块灰色的砖，如下图所示，则规约成一个子问题

第二种可能，没有灰色的砖，下面也可以横着放，那么规约成另一个子问题

处理完这一步，就可以继续处理其他的砖了，也同样是类似的步骤

代码：

 #include <cmath>
 #include <cstdio>
 #include <vector>
 #include <iostream>
 #include <algorithm>
 #include <cstring>
 using namespace std;

 #define MAX_N 128

 int N, T;
 bool can[MAX_N][MAX_N];
 bool u[MAX_N];
 bool d[MAX_N];

 int main() {
     /* Enter your code here. Read input from STDIN. Print output to STDOUT */
     cin >> T;
     while (T--) {
         cin >> N;

         memset(u, , sizeof(u));
         memset(d, , sizeof(d));
         for (int i = ; i < N; i++) {
             char c;
             cin >> c;
             u[i] = c == '' ? true : false;
         }
         for (int i = ; i < N; i++) {
             char c;
             cin >> c;
             d[i] = c == '' ? true : false;
         }

         memset(can, , sizeof(can));
         for (int i = ; i < ; i++)
             for (int j = ; j < ; j++)
                 can[N + i][N + j] = true;

         int i = N;
         int j = N;
         while (i >=  || j >= ) {
             if (--j >= ) {
                 if (!d[j]) {
                     can[i][j] = can[i][j + ];
                 } else {
                     if (u[i])
                         can[i][j] |= can[i + ][j + ];
                     if (d[j + ]) {
                         if (!u[i])
                             can[i][j] |= can[i + ][j + ];
                         if (u[i] && u[i + ])
                             can[i][j] |= can[i + ][j + ];
                     }
                 }
             }
             if (--i >= ) {
                 if (!u[i]) {
                     can[i][j] = can[i + ][j];
                 } else {
                     if (d[j])
                         can[i][j] |= can[i + ][j + ];
                     if (u[i + ]) {
                         if (!d[j])
                             can[i][j] |= can[i + ][j + ];
                         if (d[j] && d[j + ])
                             can[i][j] |= can[i + ][j + ];
                     }
                 }
             }
         }

         cout << (can[][] ? "YES" : "NO") << endl;
     }
     return ;
 }