codeforces 920 EFG 题解合集 （ Educational Codeforces Round 37 ）

E. Connected Components?

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given an undirected graph consisting of n vertices and 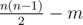 edges. Instead of giving you the edges that exist in the graph, we give you m unordered pairs (x, y) such that there is no edge between x and y, and if some pair of vertices is not listed in the input, then there is an edge between these vertices.

You have to find the number of connected components in the graph and the size of each component. A connected component is a set of vertices X such that for every two vertices from this set there exists at least one path in the graph connecting these vertices, but adding any other vertex to X violates this rule.

Input

The first line contains two integers n and m (1 ≤ n ≤ 200000, ).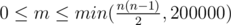

Then m lines follow, each containing a pair of integers x and y (1 ≤ x, y ≤ n, x ≠ y) denoting that there is no edge between x and y. Each pair is listed at most once; (x, y) and (y, x) are considered the same (so they are never listed in the same test). If some pair of vertices is not listed in the input, then there existsan edge between those vertices.

Output

Firstly print k — the number of connected components in this graph.

Then print k integers — the sizes of components. You should output these integers in non-descending order.

Example

input

5 5
1 2
3 4
3 2
4 2
2 5

output

2
1 4 

题意：一个无向图，给出没有连边的点对（没有给出的点对都有直接连边），求联通块个数和每个联通块的大小。

题解：首先是存边的问题，不可能把所有边都记录下来吧。那么久只能记录不连通关系了，用邻接表记录的话，询问两个点之间是否有连边不大方便。

可以给每个点开一个set，set里面存不连通关系，询问两个点之间是否有连边就在set里面查找有没有对应元素就行了。

也可以给每个点开一个map，当做邻接矩阵用。我采用的是这种。

思路：维护一个集合（set），存储当前不确定在哪个联通块中的点，初始时所有点都在里面。

然后在其中依次取点，dfs遍历它的联通块，统计一下，把遍历到的点都扔出这个集合，因为它们的连通关系已经确定，不用再对其进行dfs。

注意：dfs一个点x的时候，要寻找x的出边，这样很慢，应该在set中依次查找，判断set中的点与x是否有直接连边。

遍历set的时候不要for(set<int>iterator::it=s.begin();it!=s.end();it++)   ，由于有删除操作，还是递归删除，所以it指向的元素可能在下一层递归中被删掉，然后……就RE了。可以用lower_bound()或upper_bound()查找下一个元素，具体见代码。

 /*
 Welcome Hacking
 Wish You High Rating
 */
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<ctime>
 #include<cstdlib>
 #include<algorithm>
 #include<cmath>
 #include<string>
 #include<map>
 #include<set>
 using namespace std;
 int read(){
     int xx=,ff=;char ch=getchar();
     while(ch>''||ch<''){if(ch=='-')ff=-;ch=getchar();}
     while(ch>=''&&ch<=''){xx=(xx<<)+(xx<<)+ch-'';ch=getchar();}
     return xx*ff;
 }
 const int maxn=;
 int N,M,t1,t2,temp[maxn],ans;
 set<int>s;
 map<int,bool>e[maxn];
 void dfs(int x){
     int prev=;
     while(){
         int t=*s.lower_bound(prev);
         if(t==(<<))
             break;
         prev=t+;
         if(!e[x][t]){
             temp[ans]++;
             s.erase(t);
             dfs(t);
         }
     }
 }
 int main(){
     //freopen("in","r",stdin);
     N=read(),M=read();
     for(int i=;i<=N;i++)
         s.insert(i);
     s.insert(<<);
     for(int i=;i<=M;i++){
         t1=read(),t2=read();
         e[t1][t2]=e[t2][t1]=;
     }
     int prev=;
     while(){
         int t=*s.lower_bound(prev);
         if(t==(<<))
             break;
         prev=t+;
         s.erase(t);
         temp[++ans]=;
         dfs(t);
     }
     sort(temp+,temp++ans);
     printf("%d\n",ans);
     for(int i=;i<=ans;i++)
         printf("%d ",temp[i]);
     puts("");
     return ;
 }

F. SUM and REPLACE

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Let D(x) be the number of positive divisors of a positive integer x. For example, D(2) = 2 (2 is divisible by 1 and 2), D(6) = 4 (6 is divisible by 1, 2, 3 and 6).

You are given an array a of n integers. You have to process two types of queries:

1. REPLACE l r — for every 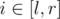 replace ai with D(ai);
2. SUM l r — calculate .

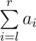Print the answer for each SUM query.

Input

The first line contains two integers n and m (1 ≤ n, m ≤ 3·105) — the number of elements in the array and the number of queries to process, respectively.

The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 106) — the elements of the array.

Then m lines follow, each containing 3 integers ti, li, ri denoting i-th query. If ti = 1, then i-th query is REPLACE li ri, otherwise it's SUM li ri (1 ≤ ti ≤ 2, 1 ≤ li ≤ ri ≤ n).

There is at least one SUM query.

Output

For each SUM query print the answer to it.

Example

input

7 6
6 4 1 10 3 2 4
2 1 7
2 4 5
1 3 5
2 4 4
1 5 7
2 1 7

output

30
13
4
22

大意：对于一个给定序列，有两种操作：

1：给定区间[L,R]，将其中的每个元素x变为D(x)

D(x)是x的因子数。

2：给定区间[L,R]，求和。

题解：

线段树套路题。

注意到在x属于1e6以内时，D(x)最大是240.

x,D(x),D(D(x))……的衰减速度非常快。

打表可知，对于一个数1e6以内的x，最多进行第一个操作6次，就会变成2（除了1  ,  D(1)=1）

先把序列中的所有1都换成2，同时记录一下，方便统计回来。

维护一个线段树记录区间内1操作数的次数的最小值和区间和

对于每个1操作，暴力修改到线段树底层，直到1操作次数最小值大于等于6.

这样修改的复杂度最差O(N*logN)   (最多修改6次，6是常数)

查询的复杂度为O(1)

UOJ round  和 hdu 上都有类似的题。

 /*
 Welcome Hacking
 Wish You High Rating
 */
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<ctime>
 #include<cstdlib>
 #include<algorithm>
 #include<cmath>
 #include<string>
 using namespace std;
 inline int read(){
     int xx=,ff=;char ch=getchar();
     while(ch>''||ch<''){if(ch=='-')ff=-;ch=getchar();}
     while(ch>=''&&ch<=''){xx=(xx<<)+(xx<<)+ch-'';ch=getchar();}
     return xx*ff;
 }
 inline int mymin(int xx,int yy)
 {if(xx<yy)return xx;return yy;}
 const int maxn=,limit=;
 int N,M,D[limit+],tot=,sum[maxn],a[maxn];
 struct Segment_Tree{
     long long sum;
 }T[maxn*];
 int x,y,opt;
 void build(int L,int R,int root){
     if(L==R){
         T[root].sum=a[L];
         return;
     }
     int mid=(L+R)>>;
     build(L,mid,root*);
     build(mid+,R,root*+);
     T[root].sum=T[root*].sum+T[root*+].sum;
 }
 void upd(int L,int R,int root){
     if(T[root].sum==(R-L+)*)
         return;
     if(x>R||y<L)
         return;
     if(L==R){
         T[root].sum=D[T[root].sum];
         return;
     }
     int mid=(L+R)>>;
     upd(L,mid,root*);
     upd(mid+,R,root*+);
     T[root].sum=T[root*].sum+T[root*+].sum;
 }
 long long query(int L,int R,int root){
     if(x>R||y<L)
         return ;
     if(x<=L&&y>=R)
         return T[root].sum;
     int mid=(L+R)>>;
     return query(L,mid,root*)+query(mid+,R,root*+);
 }
 int main(){
     //freopen("in","r",stdin);
     for(int i=;i<=limit;i++)
         for(int j=i;j<=limit;j+=i)
             D[j]++;
     N=read(),M=read();
     for(int i=;i<=N;i++){
         a[i]=read();
         sum[i]=sum[i-];
         if(a[i]==)
             a[i]=,sum[i]++;
     }
     build(,N,);
     while(M--){
         opt=read();
         if(opt==){
             x=read(),y=read();
             upd(,N,);
         }
         else{
             x=read(),y=read();
             printf("%I64d\n",query(,N,)-(sum[y]-sum[x-]));
         }
     }
     return ;
 }

G. List Of Integers

time limit per test

5 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Let's denote as L(x, p) an infinite sequence of integers y such that gcd(p, y) = 1 and y > x (where gcd is the greatest common divisor of two integer numbers), sorted in ascending order. The elements of L(x, p)are 1-indexed; for example, 9, 13 and 15 are the first, the second and the third elements of L(7, 22), respectively.

You have to process t queries. Each query is denoted by three integers x, p and k, and the answer to this query is k-th element of L(x, p).

Input

The first line contains one integer t (1 ≤ t ≤ 30000) — the number of queries to process.

Then t lines follow. i-th line contains three integers x, p and k for i-th query (1 ≤ x, p, k ≤ 106).

Output

Print t integers, where i-th integer is the answer to i-th query.

Examples

input

3
7 22 1
7 22 2
7 22 3

output

9
13
15

input

5
42 42 42
43 43 43
44 44 44
45 45 45
46 46 46

output

187
87
139
128
141

大意：t个询问，给出x,p,k求与p互质的大于x的第k个数。

G. List Of Integers

time limit per test

5 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Let's denote as L(x, p) an infinite sequence of integers y such that gcd(p, y) = 1 and y > x (where gcd is the greatest common divisor of two integer numbers), sorted in ascending order. The elements of L(x, p)are 1-indexed; for example, 9, 13 and 15 are the first, the second and the third elements of L(7, 22), respectively.

You have to process t queries. Each query is denoted by three integers x, p and k, and the answer to this query is k-th element of L(x, p).

Input

The first line contains one integer t (1 ≤ t ≤ 30000) — the number of queries to process.

Then t lines follow. i-th line contains three integers x, p and k for i-th query (1 ≤ x, p, k ≤ 106).

Output

Print t integers, where i-th integer is the answer to i-th query.

Examples

input

3
7 22 1
7 22 2
7 22 3

output

9
13
15

input

5
42 42 42
43 43 43
44 44 44
45 45 45
46 46 46

output

187
87
139
128
141

题解：二分加容斥。

每个数的因子可以用筛法筛出来。

然后就是二分查找ans，容斥原理计算ans内有多少个与p互质的数。

至于大于x嘛，只需用容斥算出小于等于x的与p互质的数有多少个，加进k里面就行了。

 /*
 Welcome Hacking
 Wish You High Rating
 */
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<ctime>
 #include<cstdlib>
 #include<algorithm>
 #include<cmath>
 #include<string>
 #include<vector>
 using namespace std;
 int read(){
     int xx=,ff=;char ch=getchar();
     while(ch>''||ch<''){if(ch=='-')ff=-;ch=getchar();}
     while(ch>=''&&ch<=''){xx=(xx<<)+(xx<<)+ch-'';ch=getchar();}
     return xx*ff;
 }
 const int limit=;
 vector<int>V[limit+];
 void get_fac(){
     for(int i=;i<=limit;i++)
         if(!V[i].size())
             for(int j=i;j<=limit;j+=i)
                 V[j].push_back(i);
 }
 int x,p,k,delta;
 int L,R,mid;
 int calc(int num,int rb){
     int siz=V[num].size();
     int re=;
     for(int i=;i<(<<siz);i++){
         int s=,tim=;
         for(int j=;j<siz;j++)
             if((i>>j)&)
                 s*=V[num][j],tim++;
         if(tim&)
             re+=rb/s;
         else
             re-=rb/s;
     }
     return rb-re;
 }
 int main(){
     //freopen("in","r",stdin);
     get_fac();
     for(int T=read();T;T--){
         x=read(),p=read(),k=read();
         delta=calc(p,x);
         L=x,R=int(1e8);
         while(L+<R){
             mid=(L+R)/;
             if(calc(p,mid)-delta>=k)
                 R=mid;
             else
                 L=mid;
         }
         printf("%d\n",R);
     }
     return ;
 }