莫比乌斯反演总结——Chemist

懵逼乌斯反演果然名不虚传，自闭了两天的我打算学习一下这一块比较实用的数论内容。

（注：1.为了区分狄尼克雷卷积与乘法，本篇文章中乘号全部省略，卷积全部用" * "表示。2.用gcd(a,b)表示a和b的最大公约数。3.用lcm(a,b)表示a和b的最小公倍数。4.用C(n,m)表示在n个数中选择m个数的方案数。5." ^ "在本篇文章中表示乘方而不是异或。）

知识点：

一、数论函数：

　　定义：定义域为正整数，(陪域为复数)的函数。

二、积性函数

　　1.定义：满足f(ab)=f(a)f(b)(gcd(a,b)=1)的数论函数。

　　*完全积性函数定义：满足f(ab)=f(a)f(b)的数论函数。

　　2.常见积性函数：（1）欧拉函数φ(n)（2）莫比乌斯函数μ(n)（3）除数函数d_k(n)表示n的所有正因子k次幂和

　　3.积性函数性质：

　　（1）设n=∏p_i^c_i ，则f(n)=∏f(p_i^c_i)，由定义显然。因此大多数积性函数可以线性筛预处理。

　　（2）若f(n)，g(n)均为积性函数，h(n)=f(n)g(n)，h(n)=f(n)/g(n)也为积性函数。

　　　证明：h(a)h(b)=f(a)g(a)f(b)g(b)=f(a)f(b)g(a)g(b)=f(ab)g(ab)=h(ab)，满足定义，得证。

　　（3）欧拉函数φ(n)的性质：(φ*1)(n)=n。

　　　证明：

　　　　(φ*1)(n)=∑_d|n φ(d)1(n/d)=∑_d|n φ(d)，

　　　　分解质因数得n=∏(i:1~k)p_i^c_i ，

　　　　由于欧拉函数为积性函数，∑_d|n φ(d)=∏(i:1~k)(∑(j:0~c_i)φ(p_i^j))，（将式子拆开显然）

　　　　由φ(1)=1得　　　∑_d|n φ(d)=∏(i:1~k)(∑(j:1~c_i)φ(p_i^j)+1)　

　　　　由φ(p^e)=(p-1)p^e-1 =p^e -p^e-1 ，可得∑_d|n φ(d)=∏(i:1~k)(∑(j:1~c_i)(p_i^j - p_i^j-1)+1)

　　　　将∑内的式子拆开得，∑_d|n φ(d)=∏p_i^c_i =n。　

三、狄尼克雷卷积

　　1.定义：两个数论函数的狄尼克雷卷积 (f*g)(n)=∑_d|n f(d)g(n/d)。

　　2.性质：

　　（1）满足交换律。

　　　感性证明：每一个数的因子都是两两对应的，所以无论是什么顺序，都会将所有的f(d)和g(n/d)的乘积都加一遍。

　　（2）满足结合律。

　　　证明如图：

　　　

　　（3）满足分配律。

　　　证明：设k(n)=g(n)+h(n)，f*(g+h)(n)=(f*k)(n)=∑_d|n f(n)k(n/d)=∑_d|n f(n)(g(n/d)+h(n/d))=∑_d|n f(n)g(n/d)+∑_d|n f(n)h(n/d)=(f*g)(n)+(f*h)(n)，得证。

　　（4）积性函数的卷积还是积性函数。

　　　证明如图：

　　　　

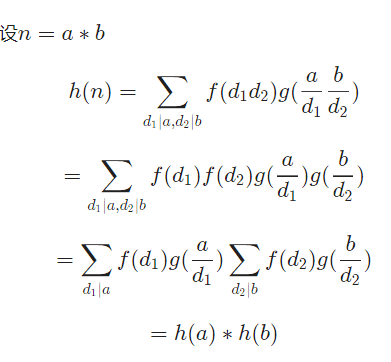
　　3.单位元：e(n)，e(1)=1，e(n)=0（n!=1）。（单位元：若对于任意的数论函数f(n)，都有(f*e)(n)=f(n)，则e(n)称为单位元。）

　　　证明：(f*e)(n)=∑_d|n f(d)e(n/d)，当且仅当d==n时，e(n/d=1)=1，因此只会在d==n时对答案有贡献，贡献为f(n)，因此(f*e)(n)=f(n)，得证。

四、莫比乌斯函数

　　（1）定义：μ(1)=1；当n含平方因子时，μ(n)=0；否则μ(n)=(-1)^k，k为n的本质不同的质因子个数。

　　（2）定义狄尼克雷卷积的单位元为e(n)，e(n)=∑_d|n μ(d)。

　　　e(n)=∑_d|n μ(d)，

　　　将n分解质因数得：n=∏(i:1~k)p_i^c_i ，令n'=∏(i:1~k)p_i ，由μ的定义可知，μ(n)的大小只与n本质不同的质因子有关，得：

　　　e(n)=∑_d|n' μ(d)，

　　　枚举d为i个质因子的乘积，在k个质因子中选择i的方案数为C(k,i)，得：

　　　e(n) = ∑(i:0~k) C(k,i)μ(i)

　　　　　= ∑(i:0~k) C(k,i)(-1)^i

　　　　　= ∑(i:0~k) C(k,i)(-1)^i 1^(k-i)

　　　根据二项式定理，原式=((-1)+1)^k，当k==0即n==1时e(n)=1，否则e(n)=0。

五、莫比乌斯反演

　　设f(n)，g(n)为两个数论函数，

　　如果有f(n)=(g*1)(n)，

　　那么有g(n)=(f*μ)(n)。

　　证明：

　　　将一式带入二式得，g(n)=(f*μ)(n)=(g*1*μ)(n)，

　　　根据卷积的结合律得，g(n)=(g*(μ*1))(n)，

　　　(μ*1)(n)=∑_d|n μ(d)=e(n)，

　　　带入上式得，g(n)=(g*e)(n)=g(n)，成立。

六、线性筛

　　前文已经提到，绝大多数积性函数可以用线性筛筛出来，下面附上线性筛筛素数，欧拉函数，莫比乌斯函数的代码：

int n,prime[N],num=0,phi[N],miu[N];
bool notprime[N];
void get()
{
	notprime[1]=1;
	phi[1]=1;
	miu[1]=1;
	for(int i=2;i<=n;i++)
	{
		if(!notprime[i]){
			prime[++num]=i;
			phi[i]=i-1;
　　　　　　　　　　　　　　 //φ(p)=p-1
			miu[i]=-1;
　　　　　　　　　　　　　　 //质数本质不同的质因子只有自己，因此μ(p)=(-1)^1=-1
		}
		for(int j=1;j<=num;j++)
		{
			if(i*prime[j]>n)break;
			notprime[i*prime[j]]=1;
　　　　　　　　　　　　　　 //每个素数只会被自己的最小质因子筛一次
			if(i%prime[j]==0){
				phi[i*prime[j]]=phi[i]*prime[j];
　　　　　　　　　　　　　　　　　　　　
				miu[i*prime[j]]=0;
　　　　　　　　　　　　　　　　　　　 //i*prime[j]含有平方因子prime[j]^2，因此μ(i*prime[j])=0
				break;//确保每个数只会被最小质因子筛一次
			}
			else {
				phi[i*prime[j]]=phi[i]*phi[prime[j]];
				miu[i*prime[j]]=miu[i]*miu[prime[j]];
　　　　　　　　　　　　　　　　　　　 //μ(n),φ(n)均满足积性函数性质
			}
		}
	}
}

七、杜教筛

　　1.作用：O(n^(2/3))地求数论函数的前缀和。

　　2.推导：

　　　设f(n)为一数论函数，

　　　我们要求S(n)=∑(i:1~n)f(i)，

　　　我们找到另一个积性数论函数g(n)，则

　　　　∑(i:1~n) (f*g)(n)=∑(i:1~n)∑_d|i g(d)f(i/d)

　　　　把d提出来得，∑(i:1~n) (f*g)(n)=∑(d:1~n)g(d)∑_d|i f(i/d)

　　　　=∑(i:1~n)g(i)∑(j:1~(n/i))f(j)=∑(i:1~n)g(i)S(n/d)

　　　根据前缀和思想，g(1)S(n)=∑(i:1~n)g(i)S(n/i)-∑(i:2~n)g(i)S(n/i)

　　　=∑(i:1~n)(g*f)(i)-∑(i:2~n)g(i)S(n/i)

　　

未完