Lightoj 1090 - Trailing Zeroes (II)

题目连接：

　　http://www.lightoj.com/volume_showproblem.php?problem=1090

题目大意：

　　给出n,r,p,q四个数字1<=n,r,p,q<=1000000，求出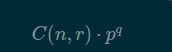的末尾有几个0？

解题思路：

　　是不是一下子懵了，数字好大，复杂度好高，精度怎么办···············，就问你怕不怕？

　　其实都是纸老虎啦，因为10的因子只有2和5，所以可以打表保存从1到当前数字相乘的积中分别含有2，5的个数。然后算出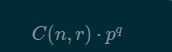中分别含有2，5的个数，取其最小就是结果。（ps：一定不要因为直接统计10的个数方便，而去统计10的个数，两者还是有不同的）。

 #include <cmath>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <iostream>
 using namespace std;
 //复杂度O(1)
 const int maxn = ;
 struct node
 {
     int x, y;
 };
 node a[maxn];
 int main ()
 {
     int t, n, r, p, q, l = ;
     memset (a, , sizeof(a));
     int x , y;
     x = y = ;
     for (int i=; i<maxn; i++)
     {//打表大法好\(^o^)/~
         int num = i;
         while (num %  == )
         {
             x ++;
             num /= ;
         }
         num = i;
         while (num %  == )
         {
             y ++;
             num /= ;
         }
         a[i].x = x;
         a[i].y = y;
     }
     scanf ("%d", &t);
     while (t --)
     {
         scanf ("%d %d %d %d", &n, &r, &p, &q);
         int res = min(a[n].x - a[r].x - a[n-r].x + (a[p].x - a[p-].x) * q, a[n].y - a[r].y - a[n-r].y + (a[p].y - a[p-].y) * q);
         printf ("Case %d: %d\n", l++, res);
     }
     return ;
 }