[Bzoj4817] [Sdoi2017]树点涂色 （LCT神题）

4817: [Sdoi2017]树点涂色

---

Time Limit: 10 Sec  Memory Limit: 128 MB
Submit: 629  Solved: 371
[Submit][Status][Discuss]

Description

---

Bob有一棵n个点的有根树，其中1号点是根节点。Bob在每个点上涂了颜色，并且每个点上的颜色不同。定义一条路

径的权值是：这条路径上的点（包括起点和终点）共有多少种不同的颜色。Bob可能会进行这几种操作：

1 x:

把点x到根节点的路径上所有的点染上一种没有用过的新颜色。

2 x y:

求x到y的路径的权值。

3 x y:

在以x为根的子树中选择一个点，使得这个点到根节点的路径权值最大，求最大权值。

Bob一共会进行m次操作

 

Input

---

第一行两个数n,m。

接下来n-1行，每行两个数a,b，表示a与b之间有一条边。

接下来m行，表示操作，格式见题目描述

1<=n,m<=100000

 

Output

---

每当出现2,3操作，输出一行。

如果是2操作，输出一个数表示路径的权值

如果是3操作，输出一个数表示权值的最大值

 

Sample Input

---

Sample Output

---

题解：

---

其实这道题考的十分妙啊，对LCT的虚实边性质进行了充分的利用。

我们读完题发现操作2可以很快想到树剖，操作3可以维护dfs序在线段树上查询子树信息。

 

但是操作1并不是树剖能解决的；

 

再来看看操作1的特点 ：每次只会修改一种从未出现的颜色，并且一定是从当前点修改到根节点。

 

然后神奇的操作就来了 ：

 

一开始我们按原树建出lct，只是lct中全部都是虚边，一个点到根节点不同 颜色数量就是它往上到根节点经过虚边数量+1。

 

每次操作1相当于就是以把当前点accees上去，这样同样颜色的就以实边连在一起了。是不是很神奇。。

 

然后再来看看怎么统计答案，我们看看lct中什么时候会变虚实边关系，当然就是access了。

 

access时我们有一句话ch[x][1] = y ，直接把x原来的右儿子覆盖了，变成了新的右儿子，

 

那么y的虚实关系从虚转为了实，只用找到y中最浅的一个点，对它子树全部贡献-1即可。

 

然后原来的右儿子从实变为了虚，找到它最浅的一个点，对它子树全部贡献+1即可。

 

然后我们来看看操作2，是对一条路径进行查询，并不能用树剖做。

 

但是我们发现一个性质，因为每次修改的颜色都是新的颜色，并且是从当前点修改到根节点，设lca（u，v） ！= u && lca（u，v） ！= v

 

那么u和v一定颜色不同，我们只需要在线段树上单询ask（u） + ask（v） -  2 * ask（lca（u，v）） +  1 即可

 

但为什么要加那个1

 

 如图，我们查询左下角颜色为1点和右下角的颜色为2的点；当lca颜色和它们不同时发现lca的颜色减多了，要加回来。

 

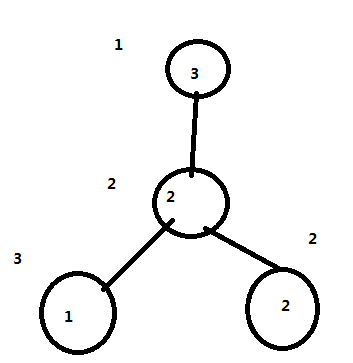
当lca和其中一个相同时，我们发现还是减多了，还是得加回来。

一条链的情况自己画图也是同理的。这样对于操作2就用线段树轻松维护了。

操作3？？？？不就是线段树dfs序查询子树吗。

这样我们就神奇的利用了LCT的性质把一道看似树剖的题做成了LCT神题。。

AC代码：

过了样例直接交，一遍交过的酸爽

---

# include <iostream>
# include <cstdio>
# include <cstring>
using namespace std;
const int N = 2e5 + ;
int st[N],ed[N],fa[N],ch[N][],s[N << ],la[N << ],n,m,head[N],dt;
struct Edge{
    int to,nex;
}edge[N << ];
void AddEdge(int u,int v)
{
    edge[++dt] = (Edge){v,head[u]};
    head[u] = dt;
}
bool isroot(int x){return ch[fa[x]][] != x && ch[fa[x]][] != x;}
void rotate(int x,int d)
{
    int pre = fa[x],g = fa[pre],nex = ch[x][d];
    ch[pre][d ^ ] = nex;
    if(nex)fa[nex] = pre;
    fa[x] = g;
    if(!isroot(pre))ch[g][ch[g][] == pre] = x;
    ch[x][d] = pre;
    fa[pre] = x;
}
void splay(int x)
{
    int pre,g;
    while(!isroot(x))
    {
        pre = fa[x],g = fa[pre];
        if(!isroot(pre) && !((ch[pre][] == x) ^ (ch[g][] == pre)))rotate(pre,ch[pre][] == x);
        rotate(x,ch[pre][] == x);
    }
}
int find(int x){while(ch[x][])x = ch[x][];return x;}
void push(int x){s[x] = max(s[x << ],s[x <<  | ]);}
void down(int x)
{
    s[x << ] += la[x];s[x <<  | ] += la[x];
    la[x <<  | ] += la[x];la[x << ] += la[x];
    la[x] = ;
}
void updata(int L,int R,int l,int r,int rt,int d)
{
    if(L <= l && r <= R){s[rt] += d;la[rt] += d;return;}
    down(rt);int mid = l + r >> ;
    if(L <= mid)updata(L,R,l,mid,rt << ,d);
    if(R > mid)updata(L,R,mid + ,r,rt <<  | ,d);
    push(rt);
}
int Query(int L,int R,int l,int r,int rt)
{
    if(L <= l && r <= R)return s[rt];
    down(rt);int mid = l + r >> ;
    if(L > mid)return Query(L,R,mid + ,r,rt <<  | );
    if(R <= mid)return Query(L,R,l,mid,rt << );
    return max(Query(L,R,l,mid,rt << ),Query(L,R,mid + ,r,rt <<  | ));
}
int ask(int x){return Query(st[x],st[x],,n,);}
void access(int x)
{
   int y = ,t;
   while(x)
  {
   splay(x);
   if(t = find(ch[x][]))updata(st[t],ed[t],,n,,);
   ch[x][] = y;if(t = find(y))updata(st[t],ed[t],,n,,-);
   y = x;x = fa[x];
  }
}
int hson[N],sz[N],tot,top[N],dep[N],Fa[N],id[N];
void dfs(int u)
{
    sz[u] = ;
    for(int i = head[u];i;i = edge[i].nex)
    {
        if(sz[edge[i].to])continue;
        Fa[edge[i].to] = u;
        dep[edge[i].to] = dep[u] + ;
        dfs(edge[i].to);
        sz[u] += sz[edge[i].to];
        if(sz[hson[u]] < sz[edge[i].to])hson[u] = edge[i].to;
    }
}
void dfs(int u,int tp)
{
    top[u] = tp;st[u] = ++tot;id[tot] = u;
    if(hson[u])dfs(hson[u],tp);
    for(int i = head[u];i;i = edge[i].nex)
    if(!st[edge[i].to])dfs(edge[i].to,edge[i].to);
    ed[u] = tot;
}
int lca(int x,int y)
{
    while(top[x] != top[y])
    {
        if(dep[top[x]] < dep[top[y]])swap(x,y);
        x = Fa[top[x]];
    }
    return dep[x] < dep[y] ? x : y;
}
int Q1(int u,int v){return ask(u) + ask(v) -  * ask(lca(u,v)) + ;}
int Q2(int u){return Query(st[u],ed[u],,n,);}
int main()
{
       scanf("%d %d",&n,&m);int tp,x,y;
       for(int i = ;i < n;i++)
       {
           scanf("%d %d",&x,&y);
           AddEdge(x,y);AddEdge(y,x);
       }
       dfs();dfs(,);
       for(int i = ;i <= n;i++)updata(st[i],ed[i],,n,,),fa[i] = Fa[i];
       while(m--)
       {
           scanf("%d",&tp);
           if(tp == )scanf("%d",&x),access(x);
           if(tp == )scanf("%d %d",&x,&y),printf("%d\n",Q1(x,y));
           if(tp == )scanf("%d",&x),printf("%d\n",Q2(x));
       }
}