BitMap的原理和实现

相关概念

　基础类型

　在java中：　　

byte  ->   8 bits  -->1字节
char  ->   16 bit  -->2字节
short ->   16 bits -->2字节
int   ->   32 bits -->4字节
float ->   32 bits -->4字节
long  ->   64 bits -->8字节

　位运算符

　　在java中，int数据底层以补码形式存储。int型变量使用32bit存储数据，其中最高位是符号位，0表示正数，1表示负数，可通过Integer.toBinaryString()转换为bit字符串，

// 若最高的几位为0则不输出这几位，从为1的那一位开始输出
System.out.println(Integer.toBinaryString(10));
System.out.println(Integer.toBinaryString(-10));
// 会输出（手工排版过，以下的输出均会被手工排版）：
                            1010
11111111111111111111111111110110

　左移<<

　　例如：5 << 2 = 20

首先会将5转为2进制表示形式: 0000 0000 0000 0000 0000 0000 0000 0101  

然后左移2位后，低位补0：    0000 0000 0000 0000 0000 0000 0001 0100
换算成10进制为20

　右移>>

　　例如： 5 >> 2 = 1

还是先将5转为2进制表示形式： 0000 0000 0000 0000 0000 0000 0000 0101
然后右移2位，高位补0：      0000 0000 0000 0000 0000 0000 0000 0001
换算成十进制后是1

　无符号右移>>>

　　　5 >>> 3　　　　

　　我们知道在Java中int类型占32位，可以表示一个正数，也可以表示一个负数。正数换算成二进制后的最高位为0，负数的二进制最高为为1。对于2进制补码的加法运算，和平常的计算一样，而且符号位也参与运算，不过最后只保留32位

-5换算成二进制： 1111 1111 1111 1111 1111 1111 1111 1011
-5右移3位：     1111 1111 1111 1111 1111 1111 1111 1111   // (用1进行补位，结果为-1)
-5无符号右移3位: 0001 1111 1111 1111 1111 1111 1111 1111   // (用0进行补位,结果536870911 )

　位与&

　　第一个操作数的的第n位于第二个操作数的第n位如果都是1，那么结果的第n为也为1，否则为0

5转换为二进制：0000 0000 0000 0000 0000 0000 0000 0101
3转换为二进制：0000 0000 0000 0000 0000 0000 0000 0011
------------------------------------------------------------
1转换为二进制：0000 0000 0000 0000 0000 0000 0000 0001

　位或|

　　第一个操作数的的第n位于第二个操作数的第n位只要有一个为1则为1，否则为0

5转换为二进制：0000 0000 0000 0000 0000 0000 0000 0101
3转换为二进制：0000 0000 0000 0000 0000 0000 0000 0011
-------------------------------------------------------------------------------------
6转换为二进制：0000 0000 0000 0000 0000 0000 0000 0111

　　对于移位运算，例如将x左移/右移n位，如果x是byte、short、char、int，n会先模32（即n=n%32），然后再进行移位操作。可以这样解释：int类型为32位,移动32位（或以上）没有意义。

　　同理若x是long，n=n%64。

　左移和右移代替乘除

a=a*4;
b=b/4;

　可以改为

a=a<<2;
b=b>>2;

　　说明： 　　除2 = 右移1位 乘2 = 左移1位 　　除4 = 右移2位 乘4 = 左移2位 　　除8 = 右移3位 乘8 = 左移3位 　　… …

　　类比十进制中的满十进一，向左移动小数点后，数字就会缩小十倍，在二进制中满二进一，进行右移一次相当于缩小了2两倍，右移两位相当于缩小了4倍，右移三位相当于缩小了8倍。通常如果需要乘以或除以2的n次方，都可以用移位的方法代替。

　　实际上，只要是乘以或除以一个整数，均可以用移位的方法得到结果如：

　　a=a*9

　　分析a9可以拆分成a(8+1)即a8+a1, 因此可以改为： a=(a<<3)+a

　　a=a*7

　　分析a7可以拆分成a(8-1)即a8-a1, 因此可以改为： a=(a<<3)-a

　　关于除法读者可以类推, 此略。

　　【注意】由于+/-运算符优先级比移位运算符高，所以在写公式时候一定要记得添加括号，不可以 a = a*12 等价于 a = a<<3 +a <<2; 要写成a = (a<<3)+(a <<2 )。

　与运算代替取余

31转换为二进制：011111,0,31
32转换为二进制：100010 与31取交集的结果是：10转换为十进制为2
31转换为二进制：100001 与31取交集的结果是：01转换为十进制为1
30转换为二进制：011110 与31取交集的结果是：11110转换为十进制为30
29转换为二进制：011101 与31取交集的结果是：11101转换为十进制为29
33转换为二进制：100001 与31取交集的结果是：1转换为十进制为1

　　31转换为二进制后，低位值全部为1，高位全为0。所以和其进行与运算，高位和0与，结果是0，相当于将高位全部截取，截取后的结果肯定小于等于31，地位全部为1，与1与值为其本身，所以相当于对数进行了取余操作。

　进制转换

• 0x开头表示16进制，例如：0x2表示：2，0x2f表示48
• 0开头表示8进制，例如：02表示：2,010表示：8

Integer.toHexString(int i)   // 十进制转成十六进制
Integer.toOctalString(int i) // 十进制转成八进制
Integer.toBinaryString(int i)// 十进制转成二进制
Integer.valueOf(m,n).toString() // 把n进制的m转换为10进制

---

BitMap实现原理　　

　　在java中，一个int类型占32个比特，我们用一个int数组来表示时未new int[32],总计占用内存32*32bit,现假如我们用int字节码的每一位表示一个数字的话，那么32个数字只需要一个int类型所占内存空间大小就够了，这样在大数据量的情况下会节省很多内存。

　具体思路：

　　1个int占4字节即4*8=32位，那么我们只需要申请一个int数组长度为 int tmp[1+N/32]即可存储完这些数据，其中N代表要进行查找的总数，tmp中的每个元素在内存在占32位可以对应表示十进制数0~31,所以可得到BitMap表:

　　　　tmp[0]:可表示0~31

　　　　tmp[1]:可表示32~63

　　　　tmp[2]可表示64~95

　　　　.......

　　那么接下来就看看十进制数如何转换为对应的bit位：

　　假设这40亿int数据为：6,3,8,32,36,......，那么具体的BitMap表示为：

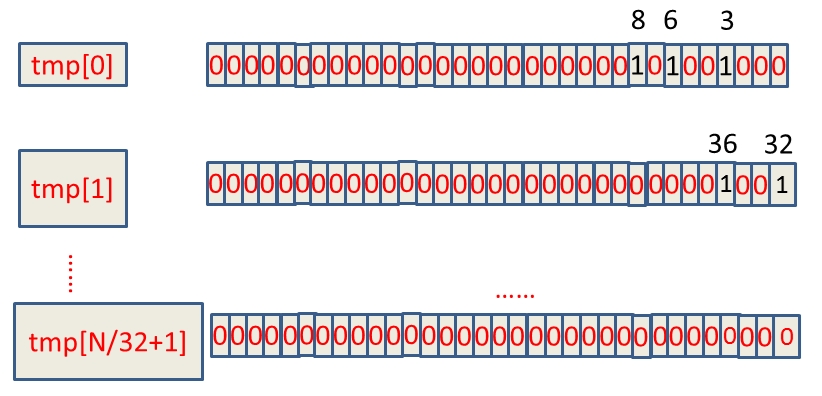
　　如何判断int数字在tmp数组的哪个下标，这个其实可以通过直接除以32取整数部分，例如：整数8除以32取整等于0，那么8就在tmp[0]上。另外，我们如何知道了8在tmp[0]中的32个位中的哪个位，这种情况直接mod上32就ok，又如整数8，在tmp[0]中的第8 mod上32等于8，那么整数8就在tmp[0]中的第八个bit位（从右边数起）。

BitMap源码

private long length;
    private static int[] bitsMap;
    private static final int[] BIT_VALUE = {0x00000001, 0x00000002, 0x00000004, 0x00000008, 0x00000010, 0x00000020,
            0x00000040, 0x00000080, 0x00000100, 0x00000200, 0x00000400, 0x00000800, 0x00001000, 0x00002000, 0x00004000,
            0x00008000, 0x00010000, 0x00020000, 0x00040000, 0x00080000, 0x00100000, 0x00200000, 0x00400000, 0x00800000,
            0x01000000, 0x02000000, 0x04000000, 0x08000000, 0x10000000, 0x20000000, 0x40000000, 0x80000000};

    public BitMap2(long length) {
        this.length = length;
        /**
         * 根据长度算出，所需数组大小
         * 当 length%32=0 时大小等于
         * = length/32
         * 当 length%32>0 时大小等于
         * = length/32+l
         */
        bitsMap = new int[(int) (length >> 5) + ((length & 31) > 0 ? 1 : 0)];
    }

    /**
     * @param n 要被设置的值为n
     */
    public void setN(long n) {
        if (n < 0 || n > length) {
            throw new IllegalArgumentException("length value "+n+" is  illegal!");
        }
        // 求出该n所在bitMap的下标,等价于"n/5"
        int index = (int) n>>5;
        // 求出该值的偏移量(求余),等价于"n%31"
        int offset = (int) n & 31;
        /**
         * 等价于
         * int bits = bitsMap[index];
         * bitsMap[index]=bits| BIT_VALUE[offset];
         * 例如,n=3时,设置byte第4个位置为1 （从0开始计数，bitsMap[0]可代表的数为：0~31，从左到右每一个bit位表示一位数）
         * bitsMap[0]=00000000 00000000 00000000 00000000  |  00000000 00000000 00000000 00001000=00000000 00000000 00000000 00000000 00001000
         * 即: bitsMap[0]= 0 | 0x00000008 = 3
         *
         * 例如,n=4时,设置byte第5个位置为1
         * bitsMap[0]=00000000 00000000 00000000 00001000  |  00000000 00000000 00000000 00010000=00000000 00000000 00000000 00000000 00011000
         * 即: bitsMap[0]=3 | 0x00000010 = 12
         */
        bitsMap[index] |= BIT_VALUE[offset];

    }
    /**
     * 获取值N是否存在
     * @return 1：存在，0：不存在
     */
    public int isExist(long n) {
        if (n < 0 || n > length) {
            throw new IllegalArgumentException("length value illegal!");
        }
        int index = (int) n>>5;
        int offset = (int) n & 31;
        int bits = (int) bitsMap[index];
        // System.out.println("n="+n+",index="+index+",offset="+offset+",bits="+Integer.toBinaryString(bitsMap[index]));
        return ((bits & BIT_VALUE[offset])) >>> offset;
    }

BitMap应用

　　1：看个小场景 > 在3亿个整数中找出不重复的整数，限制内存不足以容纳3亿个整数。

　　对于这种场景我可以采用2-BitMap来解决，即为每个整数分配2bit，用不同的0、1组合来标识特殊意思，如00表示此整数没有出现过，01表示出现一次，11表示出现过多次，就可以找出重复的整数了，其需要的内存空间是正常BitMap的2倍，为：3亿*2/8/1024/1024=71.5MB。

　　具体的过程如下：

　　扫描着3亿个整数，组BitMap，先查看BitMap中的对应位置，如果00则变成01，是01则变成11，是11则保持不变，当将3亿个整数扫描完之后也就是说整个BitMap已经组装完毕。最后查看BitMap将对应位为11的整数输出即可。

　　2:已知某个文件内包含一些电话号码，每个号码为8位数字，统计不同号码的个数。

　　8位最多99 999 999，大概需要99m个bit，大概10几m字节的内存即可。 （可以理解为从0-99 999 999的数字，每个数字对应一个Bit位，所以只需要99M个Bit==1.2MBytes，这样，就用了小小的1.2M左右的内存表示了所有的8位数的电话）　　

BitMap问题

　　BitMap 的思想在面试的时候还是可以用来解决不少问题的，然后在很多系统中也都会用到，算是一种不错的解决问题的思路。

　　但是 BitMap 也有一些局限，因此会有其它一些基于 BitMap 的算法出现来解决这些问题。

• 数据碰撞。比如将字符串映射到 BitMap 的时候会有碰撞的问题，那就可以考虑用 Bloom Filter 来解决，Bloom Filter 使用多个 Hash 函数来减少冲突的概率。
• 数据稀疏。又比如要存入(10,8887983,93452134)这三个数据，我们需要建立一个 99999999 长度的 BitMap ，但是实际上只存了3个数据，这时候就有很大的空间浪费，碰到这种问题的话，可以通过引入 Roaring BitMap 来解决。

---

 另一种方式分析BitMap

　一、问题引入　　

　　bitMap是位图，其实准确的来说，翻译成基于位的映射，举一个例子，有一个无序有界int数组{1,2,5,7},初步估计占用内存44=16字节，这倒是没什么奇怪的，但是假如有10亿个这样的数呢，10亿*4字节/(1024*1024*1024)=3.72G左右（1GB=1024MB 、1MB=1024KB 、1KB=1024B 、1B=8b）。如果这样的一个大的数据做查找和排序，那估计内存也崩溃了，有人说，这些数据可以不用一次性加载，那就是要存盘了，存盘必然消耗IO。我们提倡的是高性能，这个方案直接不考虑。

　二、问题分析

　　如果用BitMap思想来解决的话，就好很多，解决方案如下：
　　一个byte是占8个bit，如果每一个bit的值就是有或者没有，也就是二进制的0或者1，如果用bit的位置代表数组值有还是没有， 那么0代表该数值没有出现过，1代表该数组值出现过。不也能描述数据了吗？具体如下图：

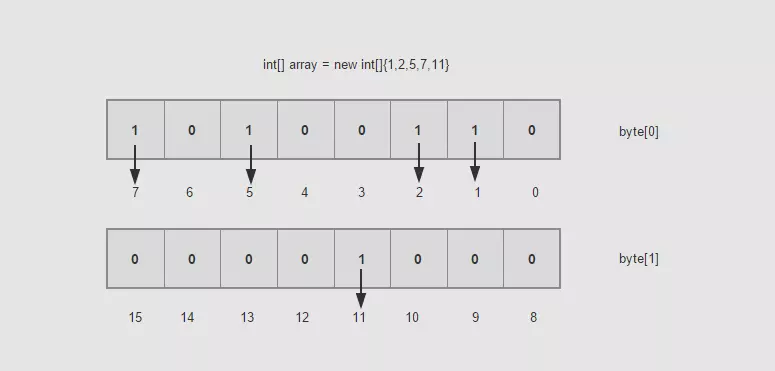
　　　　　　　　　　　　　　　　　　bitMap结构.p

　　是不是很神奇，那么现在假如10亿的数据所需的空间就是3.72G/32了吧，一个占用32bit的数据现在只占用了1bit，节省了不少的空间，排序就更不用说了，一切显得那么顺利。这样的数据之间没有关联性，要是读取的，你可以用多线程的方式去读取。时间复杂度方面也是O(Max/n)，其中Max为byte[]数组的大小，n为线程大小。

　三、应用与代码
　　如果BitMap仅仅是这个特点，我觉得还不是它的优雅的地方，接下来继续欣赏它的魅力所在。下面的计算思想其实就是针对bit的逻辑运算得到，类似这种逻辑运算的应用场景可以用于权限计算之中。

　　再看代码之前，我们先搞清楚一个问题，一个数怎么快速定位它的索引号，也就是说搞清楚byte[index]的index是多少，position是哪一位。举个例子吧，例如add(14)。14已经超出byte[0]的映射范围，在byte[1]范围之类。那么怎么快速定位它的索引呢。如果找到它的索引号，又怎么定位它的位置呢。Index(N)代表N的索引号，Position(N)代表N的所在的位置号。
　　Index(N) = N/8 = N >> 3;
　　Position(N) = N%8 = N & 0x07;

　(1) add(int num)
　　你要向bitmap里add数据该怎么办呢，不用担心，很简单，也很神奇。
　　上面已经分析了，add的目的是为了将所在的位置从0变成1.其他位置不变.

　　　　　　　　　　　　　　　　　　　　add.png

代码：

public void add(int num){
        // num/8得到byte[]的index
        int arrayIndex = num >> 3; 

        // num%8得到在byte[index]的位置
        int position = num & 0x07; 

        //将1左移position后，那个位置自然就是1，然后和以前的数据做|，这样，那个位置就替换成1了。
        bits[arrayIndex] |= 1 << position;
}

　(2) clear(int num)

　　对1进行左移，然后取反，最后与byte[index]作与操作。

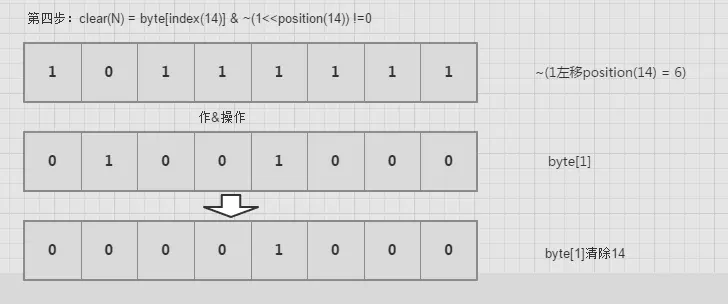
　　实例代码：

public void clear(int num){
        // num/8得到byte[]的index
        int arrayIndex = num >> 3; 

        // num%8得到在byte[index]的位置
        int position = num & 0x07; 

        //将1左移position后，那个位置自然就是1，然后对取反，再与当前值做&，即可清除当前的位置了.
        bits[arrayIndex] &= ~(1 << position); 

}

　(3) contain(int num)

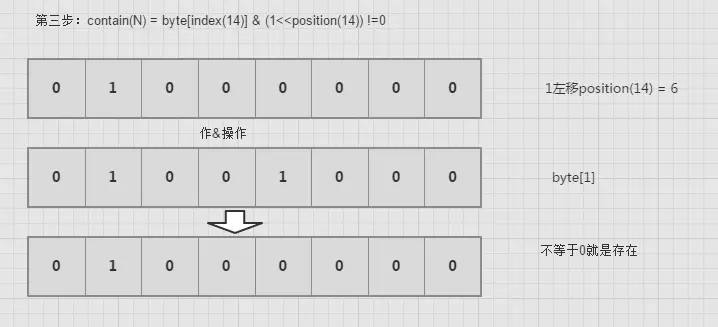
public boolean contain(int num){ // num/8得到byte[]的index
        int arrayIndex = num >> 3; // num%8得到在byte[index]的位置
        int position = num & 0x07; //将1左移position后，那个位置自然就是1，然后和以前的数据做&，判断是否为0即可
        return (bits[arrayIndex] & (1 << position)) !=0;
}

全部代码：

public class BitMap {
    //保存数据的
    private byte[] bits;

    //能够存储多少数据
    private int capacity;

    public BitMap(int capacity){
        this.capacity = capacity;

        //1bit能存储8个数据，那么capacity数据需要多少个bit呢，capacity/8+1,右移3位相当于除以8
        bits = new byte[(capacity >>3 )+1];
    }

    public void add(int num){
        // num/8得到byte[]的index
        int arrayIndex = num >> 3; 

        // num%8得到在byte[index]的位置
        int position = num & 0x07; 

        //将1左移position后，那个位置自然就是1，然后和以前的数据做|，这样，那个位置就替换成1了。
        bits[arrayIndex] |= 1 << position;
    }

    public boolean contain(int num){
        // num/8得到byte[]的index
        int arrayIndex = num >> 3; 

        // num%8得到在byte[index]的位置
        int position = num & 0x07; 

        //将1左移position后，那个位置自然就是1，然后和以前的数据做&，判断是否为0即可
        return (bits[arrayIndex] & (1 << position)) !=0;
    }

    public void clear(int num){
        // num/8得到byte[]的index
        int arrayIndex = num >> 3; 

        // num%8得到在byte[index]的位置
        int position = num & 0x07; 

        //将1左移position后，那个位置自然就是1，然后对取反，再与当前值做&，即可清除当前的位置了.
        bits[arrayIndex] &= ~(1 << position); 

    }

    public static void main(String[] args) {
        BitMap bitmap = new BitMap(100);
        bitmap.add(7);
        System.out.println("插入7成功");

        boolean isexsit = bitmap.contain(7);
        System.out.println("7是否存在:"+isexsit);

        bitmap.clear(7);
        isexsit = bitmap.contain(7);
        System.out.println("7是否存在:"+isexsit);
    }
}

出处：　https://my.oschina.net/freelili/blog/2885263

　　　　http://www.cnblogs.com/wuhuangdi/p/4126752.html#3074215