[洛谷P4183][USACO18JAN]Cow at Large P

题目链接

Bzoj崩了之后在洛谷偶然找到的点分好题！

---

在暴力的角度来说，如果我们$O(n)$枚举根节点，有没有办法在$O(n)$的时间内找到答案呢？

此时如果用树形$dp$的想法，发现是可做的，因为可以推得以下的结论：

设$x$为根节点，$d[i]$为$i$节点到$x$的距离(即深度)，$g[i]$为$i$节点到最近的出入口(即叶子节点)的距离，$ans_{x}$为以$x$为根节点时的答案。

如果$d[i] \geq g[i]$，则我们可以确定，以$i$为子树，对于$x$为根时的答案贡献为$1$。

如下图：

在对于以$i$为根的子树，会对$ans_{x}$产生$1$的贡献，可以理解为一个人从$i$为根的子树的任意叶子节点出发，可以比贝茜更先到达$i$

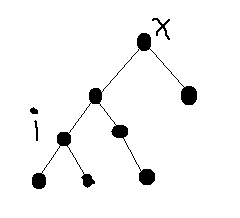
而这种解法只需要先$dfs$两次得到$g[i]$和$d[i]$，然后一次$dfs$得到答案，复杂度为$O(n^{2})$。

但是这种做法不够理想，我们还想更快的实现。

如果我们对树的性质较为熟悉，我们知道：

$1$.对于树的某棵子树，子树有m个节点，有：$\sum du[i]=2*m-1$

$2$.对于某棵树，树有n个节点，有：$\sum du[i]=2*n-2$

$PS$：$du[i]$为$i$节点的度。

将性质$1$变形为：$1=\sum (2-du[i])$

在本题中，贡献为1的子树有一个性质，即：$d[i] \geq g[i]\& \&d[fa[i]]<g[fa[i]]$。可以理解为他的父亲贡献为子节点个数，即上图中的$i$的父亲。

所以$ans_{x}$=贡献为1的子树数量之和。这不是废话吗......

所以根据性质$1$，有：$ans_{x}=\sum_{i=1}^{n}[d[i] \geq g[i]](2-du[i])$，稍微解释一下式子的来由：

因为子树的$\sum (2-du[i])=1$，而$1$刚好是一颗子树的贡献，所以满足$d[i] \geq g[i]$的点集，可以组成$ans_{x}$那么多棵贡献为1的子树。如下图：

所以满足$g[i] \geq d[i]$的点集为上图圈出来的点，而答案为贡献为1的子树数量：$3$。

---

此时我们可以用点分治的想法，将：

$ans_{x}=\sum_{i=1}^{n}[d[i] \geq g[i]](2-du[i])$

求解问题变化成求解点对问题：

$ans_{x}=\sum_{i=1}^{n}[dis(x,i) \geq g[i]](2-du[i])$，$dis(x,i)$为$x$到$i$的距离。

所以设$w$为当前子树的重心，$p[i]$为$i$到重心的距离。

则$dis(x,i) \geq g[i]\rightarrow p[x]+p[i] \geq g[i]\rightarrow p[x] \geq g[i]-p[i]$

而在每次求出$p[i]$后，可以使用树状数组维护$g[i]-p[i]$，不过注意$g[i]-p[i]$会小于0，所以维护时向右移$n$的数量。

细节问题可以看代码，其余的问题欢迎提问。

 #include <bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const int maxn = 1e5 + 5e4;
 const int inf = 2e9 + ;
 struct node {
     int s, e, w, next;
 }edge[maxn];
 int head[maxn], len;
 void init() {
     memset(head, -, sizeof(head));
     len = ;
 }
 void add(int s, int e) {
     edge[len].s = s;
     edge[len].e = e;
     edge[len].next = head[s];
     head[s] = len++;
 }
 int root, lens, sum;
 int d[maxn], du[maxn], o[maxn], vis[maxn], g[maxn], son[maxn], siz[maxn], ans[maxn];
 int rt[maxn], n;
 int lowbit(int x) {
     return x & -x;
 }
 void Add(int x, int val) {
     for (int i = x; i <=  * n; i += lowbit(i))
         rt[i] += val;
 }
 int query(int x) {
     int ans = ;
     for (int i = x; i > ; i -= lowbit(i))
         ans += rt[i];
     return ans;
 }
 void getroot(int x, int fa) {
     siz[x] = , son[x] = ;
     for (int i = head[x]; i != -; i = edge[i].next) {
         int y = edge[i].e;
         if (y == fa || vis[y])continue;
         getroot(y, x);
         siz[x] += siz[y];
         son[x] = max(son[x], siz[y]);
     }
     son[x] = max(son[x], sum - siz[x]);
     if (son[x] < son[root])root = x;
 }
 void getd(int x, int fa) {
     o[++lens] = x;
     for (int i = head[x]; i != -; i = edge[i].next) {
         int y = edge[i].e;
         if (y == fa || vis[y])continue;
         d[y] = d[x] + ;
         getd(y, x);
     }
 }
 void cal(int x, int val, int add) {
     lens = , d[x] = val;
     getd(x, );
     for (int i = ; i <= lens; i++)
         Add(g[o[i]] - d[o[i]] + n,  - du[o[i]]);
     for (int i = ; i <= lens; i++)
         ans[o[i]] += add * query(d[o[i]] + n);
     for (int i = ; i <= lens; i++)
         Add(g[o[i]] - d[o[i]] + n, du[o[i]] - );
 }
 void solve(int x) {
     cal(x, , );
     vis[x] = ;
     for (int i = head[x]; i != -; i = edge[i].next) {
         int y = edge[i].e;
         if (vis[y])continue;
         cal(y, , -);
         sum = siz[y];
         root = ;
         getroot(y, );
         solve(root);
     }
 }
 void dfs1(int x, int fa, int dep) {     g[x] = inf;
     if (du[x] == )g[x] = ;
     for (int i = head[x]; i != -; i = edge[i].next) {
         int y = edge[i].e;
         if (y == fa)continue;
         dfs1(y, x, dep + );
         g[x] = min(g[x], g[y] + );
     }
 }
 void dfs2(int x, int fa) {
     for (int i = head[x]; i != -; i = edge[i].next) {
         int y = edge[i].e;
         if (y == fa)continue;
         g[y] = min(g[y], g[x] + );
         dfs2(y, x);
     }
 }
 int main() {
     scanf("%d", &n);
     init();
     for (int i = , x, y; i < n; i++) {
         scanf("%d%d", &x, &y);
         add(x, y);
         add(y, x);
         du[x]++, du[y]++;
     }
     dfs1(, , );
     dfs2(, );
     son[] = n, root = , sum = n, getroot(, );
     solve(root);
     for (int i = ; i <= n; i++) {
         if (du[i] == )printf("1\n");
         else printf("%d\n", ans[i]);
     }
 }