HDU 1724 Ellipse (自适应辛普森积分)

题目链接：HDU 1724

Problem Description

Math is important!! Many students failed in 2+2’s mathematical test, so let's AC this problem to mourn for our lost youth..

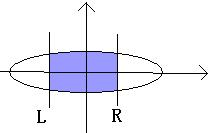
Look this sample picture:

A ellipses in the plane and center in point O. the L,R lines will be vertical through the X-axis. The problem is calculating the blue intersection area. But calculating the intersection area is dull, so I have turn to you, a talent of programmer. Your task is tell me the result of calculations.(defined PI=3.14159265 , The area of an ellipse A=PIab )

Input

Input may contain multiple test cases. The first line is a positive integer N, denoting the number of test cases below. One case One line. The line will consist of a pair of integers a and b, denoting the ellipse equation \(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\), A pair of integers l and r, mean the L is (l, 0) and R is (r, 0). (-a <= l <= r <= a).

Output

For each case, output one line containing a float, the area of the intersection, accurate to three decimals after the decimal point.

Sample Input

2
2 1 -2 2
2 1 0 2

Sample Output

6.283
3.142

Source

HZIEE 2007 Programming Contest

Solution

题意

给定椭圆和两条直线，求上图阴影部分的面积。

思路

自适应辛普森积分

Simpson 积分是数值计算中用来近似求解积分值的一种方法。公式如下：

\[\int_a^bf(x)dx \approx \frac{b - a}{a}(f(a) + 4f(\frac{a + b}{2}) + f(b))
\]

普通的 Simpson 积分误差比较大，一般使用自适应 Simpson 积分。

代码中的自适应 Simpson 积分来自 Kuangbin 的模板。

Code

#include <bits/stdc++.h>
using namespace std;
typedef double db;
const db eps = 1e-8;
db a, b, l, r;

db F(db x) {
    return sqrt((1 - x * x / a / a) * b * b);
}

db simpson(db a, db b) {
    db c = a + (b - a) / 2;
    return (F(a) + 4 * F(c) + F(b)) * (b - a) / 6;
}

db asr(db a, db b, db eps, db A) {
    db c = a + (b - a) / 2;
    db L = simpson(a, c), R = simpson(c, b);
    if(fabs(L + R - A) <= 15 * eps) return L + R + (L + R - A) / 15.0;
    return asr(a, c, eps / 2, L) + asr(c, b, eps / 2, R);
}

db asr(db a, db b, db eps) {
    return asr(a, b, eps, simpson(a, b));
}

int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        scanf("%lf%lf%lf%lf", &a, &b, &l, &r);
        printf("%.3lf\n", 2.0 * asr(l, r, eps));
    }
    return 0;
}