[Git] 023 Re：从零开始的 rebase 命令

1. 开门见山

• 我新建了一个本地仓库，并进行了一些操作
• 当前情况

• 查看（直观但不明了）

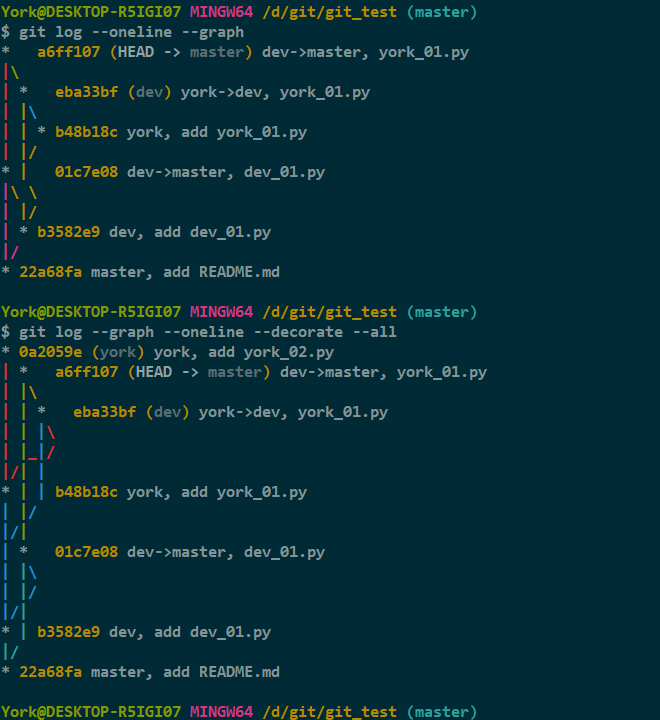
• 上图的第二条 "log" 命令详见 [Git] 024 log 命令的补充 的 "1"
• 如果我只想看 "york" 分支，可以使用 git rebase <branch_name>

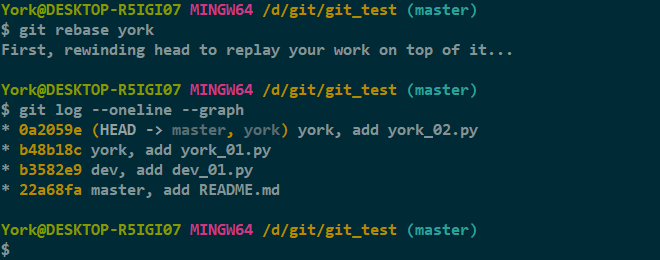
• 可以看出，"york" 这条线被理清了，并且没有层级
• 其实 "rebase" 操作是把本地未 "push" 的分叉提交历史整理成直线，使我们更容易地查看历史提交的变化

2. 恢复

• 方法不止一种，我暂且介绍一种
• 使用 git reflog 找到 "rebase" 的前一个“指针”

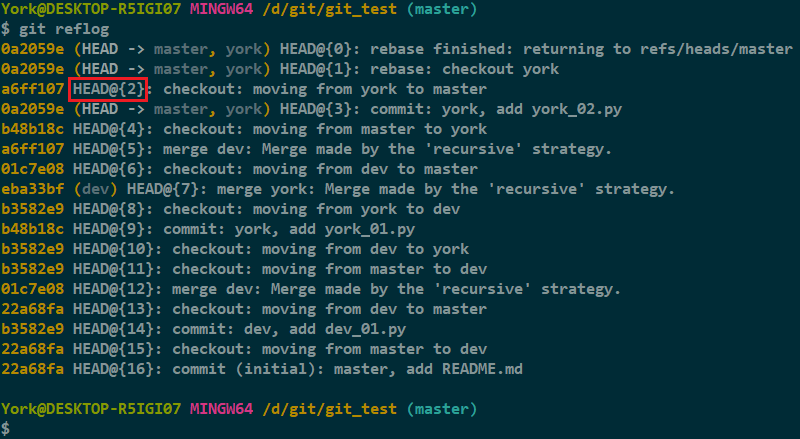
• 使用 git reset --hard HEAD@{n}

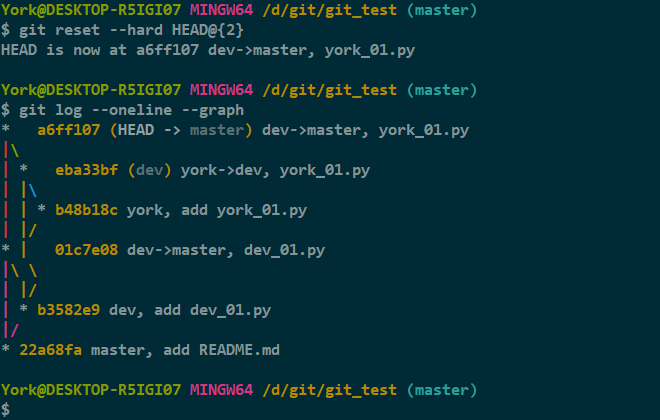
3. 进门挖坑

• "git" 官方文档的 "rebase"
• 概要

git rebase [-i | --interactive] [<options>] [--exec <cmd>] [--onto <newbase>]
    [<upstream> [<branch>]]
git rebase [-i | --interactive] [<options>] [--exec <cmd>] [--onto <newbase>]
    --root [<branch>]
git rebase --continue | --skip | --abort | --quit | --edit-todo | --show-current-patch

• 说实话，官方文档写得是真的详细！

• 本想挖几个坑的，现在看来，我目前的“地皮”不够挖那些个坑！以后用到了，慢慢更吧