清北学堂北京大学吴耀轩神仙讲课day5摘要

今天讲图论

图是啥？（白纸上的符号？）

对于一个拥有n个顶点的无向连通图，它的边数一定多于n-1条。若从中选择n-1条边，使得无向图仍然连通，则由n个顶点及这 n-1条边（弧）组成的图被称为原无向图的生成树。

换句话说，有边有点就是图。（本蒟蒻的理解是这样。。QWQ）

另外，还有一些与图有关的定义（很好理解，通俗一点）：

阶：图中点的个数。

边：两个点间的连接

权值：边的长度

。。。想了解更多找度娘，她可能讲的比我通俗QWQ。

邻接矩阵：

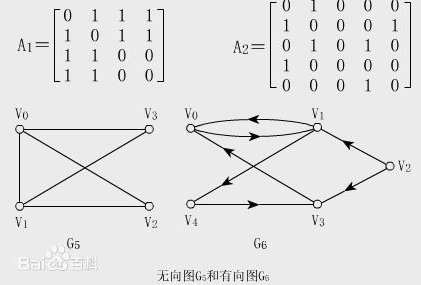
存图方式：邻接矩阵，链式前向星

1.邻接矩阵：用两个角标存储，f[i][j]表示从i到j的边的权值

2.链式前向星：

void addedge(long long from,long long to,long long dis)//入边链式前向星
{
    num_edge++;//编号
    edge[num_edge].next=head[from];//把next值改为此边编号
    edge[num_edge].to=to;//to和dis分别为对应的终点和长度
    edge[num_edge].dis=dis;
    head[from]=num_edge;//把这个边的始点的编号的head值改为前一个边的编号（指向）
}

最小生成树：从图中选出一些边和结点，使得每个结点都被联通，且保证边权之和最小

克鲁斯卡尔：

最短路径算法：

floyd：

代码为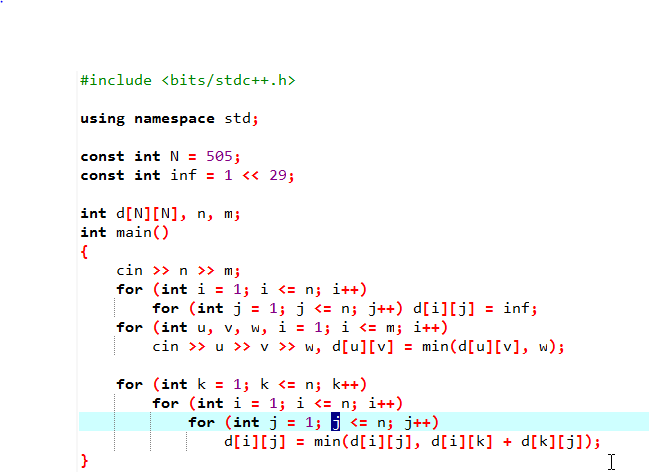三重循环

比尔曼福德：

Bellman - ford算法是求含负权图的单源最短路径的一种算法，效率较低，代码难度较小。其原理为连续进行松弛，在每次松弛时把每条边都更新一下，若在n-1次松弛后还能更新，则说明图中有负环，因此无法得出结果，否则就完成。

DAG（大哥）：