寒武纪-1005 Travel(树形DP)

一、题目链接

　　http://aiiage.hustoj.com/problem.php?id=1005

二、题面

　　PDF：http://aiiage.hustoj.com/upload/file/20180114/20180114145400_75397.pdf

　　

三、思路

　　正赛时，我一开始写了个感觉在$O(N*N*k)$的时间复杂度内做了优化的代码，交上去，TLE。尝试了各种可能的情况，还是TLE。赛后，看了官方题解。如下：

　　

　　然而，2.3的“相对直观的想法”，实在是没想到一个时间复杂度在$O(N*k*k)$的DP算法。

　　后来，队友问了其他一位AC的同学，他给我们仔细地讲了如何做DP推导。我算是听明白了。具体如下：

　　1、改掉题解中$dp$数组的意义。$dp[i][j][k]$表示：在模$k$意义下，到达结点$i$距离为$j$的结点的个数。

　　2、修改dp的含义后，设置两个$dp$数组：

　　　　（1）$dp1[3001][101][101]$。$dp1[i][j][k]$表示在以$i$为根的子树中，在模$k$意义下到达结点$i$的距离为$j$的结点的个数。

　　　　（2）$dp[3001][101][101]$。$dp[i][j][k]$表示，在模$k$意义下到达结点$i$距离为$j$的结点的个数。

　　3、$dp1$数组的递推式不难想到，假设当前结点为$root$：\[dp1[root][j][k] = \sum_i dp1[son_i][j - w_i][k]\]　

　　我们只需要以任意结点$r$为根，使用dfs搜索一遍即可求出所有结点的$dp1$的值。

　　4、然后，最关键的就是$dp$数组的推导了。如下图所示，要求$dp[x][j][k]$时，还必须知道除以结点$x$为根的子树之外的到结点$x$的距离为$j$(在模$k$意义下)的结点的个数。因为$dp[r][i]][j] = dp1[r][i][j] (0 <= i < j, 2 <= j < k)$，所以，由第一次dfs求出的数组$dp1$，即可知道$dp[r][j][k]$，由$dp[r][j][k]$推导$dp[x][j][k]$的思路是：由于结点$x$的父结点$r$的$dp$数组已知，所以，要求除以结点$x$为根的子树$t$之外的其他结点到结点$x$的距离为$j$(在模$k$意义下)的个数，只需要用$dp[r][j - w][k]$(在模$k$意义下到结点$r$距离为$j-w$的点的个数)减去$dp1[x][j - 2 * w][k]$(到结点$r$的距离为$j-w$，对于子树$t$之外的点，到达结点$x$的距离为$j$；对于子树$t$之内的点，到达结点$x$的距离为$(j - w) - w$。所以是$j - 2 * w$)，再加上$dp1[x][j][k]$，即得到了$dp[x][j][k]$。这个地方比较绕，需要结合图示好好理解。

　　

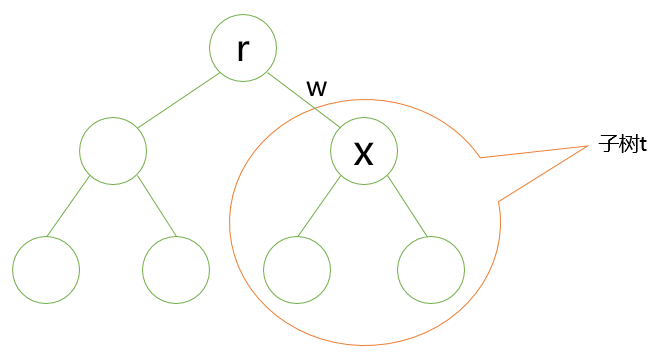
　　用数学语言表达即为：\[dp[x][j][k] = dp[r][j-w][k] - dp1[x][j - 2 * w][k] + dp1[x][j][k]\]

四、注意事项

　　1、这题时间和空间都卡得非常紧，注意在dfs的时候，一定要把当前结点下所有$j$和所有$k$的$dp1$和$dp$数组计算完。注意，千万不要在dfs外面套两层循环再传参；这题很好地体现了大量递归调用带来的开销；

　　2、题解中说，$dp$数组定义为$bool$类型，我想了很久，还是没想到，如果用$bool$类型定义$dp$数组，该如何递推(T_T，说到底还是自己功力不够啊)。如果按照上述思路写代码，$dp$数组的类型设置成$short$最好，因为点数最多就3k个。用$int$肯定会超内存。

　　3、下面的代码中，第一份是我的，写好后，无论如何优化都是超时。后来加了个编译器-O2优化，1100+ms AC了。第二份是我队友的，不晓得他的代码怎么搞的，感觉思路和代码结构都一样，他的代码不加编译器-O2优化1100+ms AC。加了编译器-O2优化，在加输入挂，300+ms AC。跑的贼快！

　　4、注意递推式中涉及减法操作，在取模时需要注意。

五、源代码

　　1、我的

#pragma GCC optimize(2)
#pragma comment(linker, "/STACK:102400000, 102400000")
#include<bits/stdc++.h>
using namespace std;
#define MAXN 3001
typedef struct {
    int to, next, wt;
} Edge;
Edge tree[MAXN << ];
int head[MAXN], ecnt;
][], dp[MAXN][][];
int N, Q;

void init() {
    memset(head, -, sizeof(head));
    ecnt = ;
}

template <class T> inline void read(T &x) {
    int t;
    bool flag = false;
    ')) ;
    if(t == '-') flag = true, t = getchar();
    x = t - ';
     + t - ';
    if(flag) x = -x;
}

void add(int from, int to, int wt) {
    tree[ecnt].to = to;
    tree[ecnt].wt = wt;
    tree[ecnt].next = head[from];
    head[from] = ecnt++;
}

void dfs0(int root, int par) {
    int  to, i, j, k;
    ; i = tree[i].next) {
        to = tree[i].to;
        if(to != par) {
            dfs0(to, root);
            ; j < ; ++j) {
                ; k <= ; ++k) {
                    dp1[root][j][k] += dp1[to][(j + k - tree[i].wt % k) % k][k];
                }
            }
        }
    }
}

void dfs1(int root, int par) {
    )memcpy(dp[], dp1[], ]));
    int to, i, j, k;
    ; i = tree[i].next) {
        to = tree[i].to;
        if(to != par) {
            ; j < ; ++j) {
                ; k <= ; ++k) {
                    dp[to][j][k] = dp[root][(j + k - (tree[i].wt % k)) % k][k] - dp1[to][(j +  * k -  * (tree[i].wt % k)) % k][k]
                                   + dp1[to][j][k];
                }
            }
            dfs1(to, root);
        }
    }
}

int main() {
//    freopen("input.txt", "r", stdin);
//    freopen("output.txt", "w", stdout);

    int a, b, c, v, k, i, j, u, m, dis;
    scanf("%d", &N);
    init();
    ; i < N; ++i) {
        read(a), read(b), read(c);
        add(a, b, c);
        add(b, a, c);
    }
    ; u <= N; ++u) {
        ; m <= ; ++m) {
            dp1[u][][m] = );
        }
    }
    dfs0(, -);
    dfs1(, -);
    read(Q);
    while(Q--) {
        read(v), read(k);
        ; dis >= ; --dis) {
            ) {
                printf("%d\n", dis);
                break;
            }
        }
    }
    ;
}

　　2、队友的

#pragma GCC optimize(2)
#pragma comment(linker, "/STACK:102400000, 102400000")
#include <bits/stdc++.h>
using namespace std;

], cnt;
struct e {
    short next, to, v;
} edge[];
void add(short a, short b, short c) {
    edge[++cnt].to = b;
    edge[cnt].next = head[a];
    edge[cnt].v = c;
    head[a] = cnt;
}
][];
][][];
][][];

];

void getfa(short u, short pre) {
    short w;
    ; i = edge[i].next) {
        short v = edge[i].to;
        if(v == pre) {w = edge[i].v; continue;}
        fa[v] = u;
        getfa(v, u);
    }
    ) {
        ; k <= ; k++) {
            ; j < k; j++) {
                dp[u][j][k] += dp1[u][j][k];
            }
        }
        return ;
    } else {
        ; k <= ; k++)
            ; j < k; j++)
                dp1[pre][j][k] += dp1[u][(j - w % k + k) % k][k];
    }
}

void dfs(short u) {
    ; i = edge[i].next) {
        short w = edge[i].v;
        short v = edge[i].to;
        if(v == fa[u])continue;
        ; k <= ; k++) {
            ; j < k; j++) {
                dp[v][j][k] = dp1[v][j][k] +
                              dp[u][(j - w % k + k) % k][k] -
                              dp1[v][(j - ( * w) % k +  * k) % k][k];
            }
        }
        dfs(v);
    }
}

template <class T> inline void read(T &x) {
    int t;
    bool flag = false;
    ')) ;
    if(t == '-') flag = true, t = getchar();
    x = t - ';
     + t - ';
    if(flag) x = -x;
}

int main() {
    int n;
    memset(head, -, sizeof(head));
    read(n);
    int u, v, w;
    ; i < n; i++) {
        read(u), read(v), read(w);
        add(u, v, w);
        add(v, u, w);
    }
    ; u <= n; u++)
        ; k <= ; k++)
            dp1[u][][k] = ;
    getfa(, -);
    dfs();
    ; u <= n; u++) {
        ; k <= ; k++) {
            ; j; j--) {
                if(dp[u][j][k]) {
                    ans[u][k] = j;
                    break;
                }
            }
        }
    }
    int q;
    read(q);
    while(q--) {
        read(u), read(w);
        printf("%d\n", ans[u][w]);
    }
    ;
}