徐州网络赛G-Trace【线段树】

There's a beach in the first quadrant. And from time to time, there are sea waves. A wave ( xx , yy ) means the wave is a rectangle whose vertexes are ( 00 , 00 ), ( xx , 00 ), ( 00 , yy ), ( xx , yy ). Every time the wave will wash out the trace of former wave in its range and remain its own trace of ( xx , 00 ) -> ( xx , yy ) and ( 00 , yy ) -> ( xx , yy ). Now the toad on the coast wants to know the total length of trace on the coast after n waves. It's guaranteed that a wave will not cover the other completely.

Input

The first line is the number of waves n(n \le 50000)n(n≤50000).

The next nn lines，each contains two numbers xx yy ,( 0 < x0<x , y \le 10000000y≤10000000 )，the ii-th line means the ii-th second there comes a wave of ( xx , yy ), it's guaranteed that when 1 \le i1≤i , j \le nj≤n ，x_i \le x_jxi​≤xj​ and y_i \le y_jyi​≤yj​ don't set up at the same time.

Output

An Integer stands for the answer.

Hint：

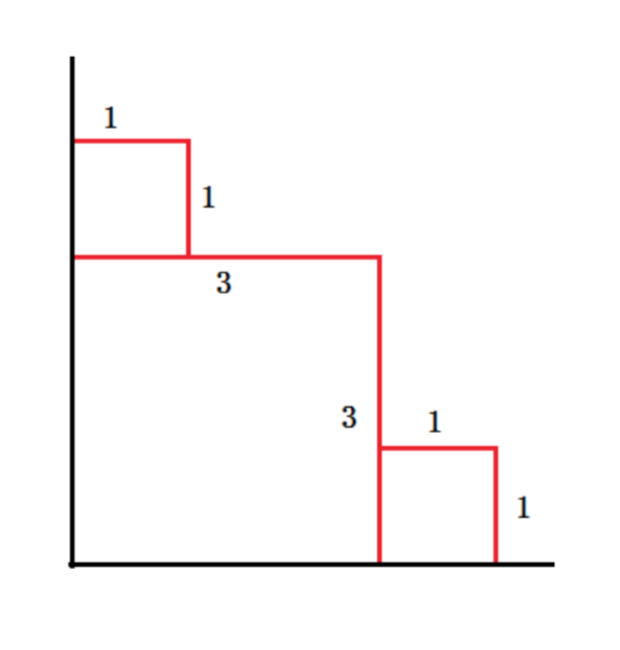
As for the sample input, the answer is 3+3+1+1+1+1=103+3+1+1+1+1=10

样例输入复制

3
1 4
4 1
3 3

样例输出复制

10

题目来源

ACM-ICPC 2018 徐州赛区网络预赛

题意：

每次给一个点 与原点画一个矩形 后面的矩形会覆盖前面的矩形

求所有露在外面的矩形的边的长度之和

思路：

线段树 将横线和竖线分开

以横线为例

从后往前 当前这条横线对结果的贡献 = 本身的长度 - 被之前的（也就是后来的矩形）遮掉的长度

后来的矩形的横线这有在这条横线之上才会对这条横线有影响

树存放当前y坐标到无穷大之间 横线的最大长度

首先离散化所有的xy坐标

从后往前处理点 查询当前y坐标之上的横线最大长度

结果加上当前横线长度-查询所得

更新y节点的值为当前横线长度

初始化树的节点都是0 做一个更新一个 build都不需要

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<stack>
#include<queue>
#include<map>
#include<vector>
#include<set>
//#include<bits/stdc++.h>
#define inf 0x7f7f7f7f7f7f7f7f
using namespace std;
typedef long long LL;

const int maxn = 50005;
int n;
struct node {
	int x, y;
}nodes[maxn];
map<int, int> newx, newy;//离散化xy坐标
set<int>xx, yy;
set<int>::iterator it;
int treex[maxn << 2], treey[maxn << 2];

void pushupx(int rt)
{
	treex[rt] = max(treex[rt << 1], treex[rt << 1 | 1]);
}

void pushupy(int rt)
{
	treey[rt] = max(treey[rt << 1], treey[rt << 1 | 1]);
}

void updatex(int x, int val, int l, int r, int rt)
{
	if (l == r) {
		treex[rt] = val;
		return;
	}
	int m = (l + r) / 2;
	if (x <= m) {
		updatex(x, val, l, m, rt << 1);
	}
	else {
		updatex(x, val, m + 1, r, rt << 1 | 1);
	}
	pushupx(rt);
}

void updatey(int x, int val, int l, int r, int rt)
{
	if (l == r) {
		treey[rt] = val;
		return;
	}
	int m = (l + r) / 2;
	if (x <= m) {
		updatey(x, val, l, m, rt << 1);
	}
	else {
		updatey(x, val, m + 1, r, rt << 1 | 1);
	}
	pushupy(rt);
}

LL queryx(int L, int R, int l, int r, int rt)
{
	if (L <= l && R >= r) {
		return treex[rt];
	}
	int m = (l + r) / 2;
	LL ans = 0;
	if (L <= m) {
		ans = max(ans, queryx(L, R, l, m, rt << 1));
	}
	if (R > m) {
		ans = max(ans, queryx(L, R, m + 1, r, rt << 1 | 1));
	}
	return ans;
}

LL queryy(int L, int R, int l, int r, int rt)
{
	if (L <= l && R >= r) {
		return treey[rt];
	}
	int m = (l + r) / 2;
	LL ans = 0;
	if (L <= m) {
		ans = max(ans, queryy(L, R, l, m, rt << 1));
	}
	if (R > m) {
		ans = max(ans, queryy(L, R, m + 1, r, rt << 1 | 1));
	}
	return ans;
}

void init()
{
	memset(treex, 0, sizeof(treex));
	memset(treey, 0, sizeof(treey));
	newx.clear();
	newy.clear();
	xx.clear();
	yy.clear();
}

int main()
{
	while (scanf("%d", &n) != EOF) {
		init();
		for (int i = 0; i < n; i++) {
			scanf("%d%d", &nodes[i].x, &nodes[i].y);
			xx.insert(nodes[i].x);
			yy.insert(nodes[i].y);
		}

		int cntx = 1, cnty = 1;
		for (it = xx.begin(); it != xx.end(); it++) {
			newx[*it] = cntx++;
		}
		cntx--;
		for (it = yy.begin(); it != yy.end(); it++) {
			newy[*it] = cnty++;
		}
		cnty--;

		LL ans = 0;
		//buildx(1, cnty, 1);
		//buildy(1, cntx, 1);
		for (int i = n - 1; i >= 0; i--) {
			int nowy = newy[nodes[i].y], nowx = newx[nodes[i].x];
			LL resx = queryx(nowy + 1, cnty, 1, cnty, 1), resy = queryy(nowx + 1, cntx, 1, cntx, 1);
			ans += nodes[i].x - resx + nodes[i].y - resy;
			updatex(nowy, nodes[i].x, 1, cnty, 1);
			updatey(nowx, nodes[i].y, 1, cntx, 1);
		}

		printf("%lld\n", ans);
	}
	return 0;
}